1. Free electrons in a magnetic field
- How does the electron density of states change in the free electron model when a magnetic field is applied?
- How does the specific heat in the free electron model change when an magnetic field is applied?
- Why does the longitudinal resistivity $\rho_{xx}$ go to zero in the Quantum Hall effect?
Solution
How does the electron density of states change in the free electron model when a magnetic field is applied?
For free electrons in 2D the density of states without an external magnetic field is given by:
\begin{equation*} D(E) = \frac{m}{\pi \hbar^2}. \end{equation*}In the presence of a magnetic field the energy levels are bunched into discrete values (Landau levels, see http://lampz.tugraz.at/~hadley/ss2/IQHE/landau.php) at energies
\begin{align*} \left(\nu + \frac{1}{2}\right) \Delta E \end{align*}where
\begin{align*} \nu = 0,1,2,\ldots & \ \text{and}\ \Delta E = \hbar \omega_c \ \text{with}\ \omega_c = \frac{eB}{m}. \end{align*}Since the total number of states must remain the same, the number of states per Landau level (i.e. the degeneracy of the Landau levels) is given by
\begin{equation*} D(E)\hbar\omega_c = \frac{m}{\pi \hbar^2} \hbar\frac{eB}{m} = \frac{2eB}{h}. \end{equation*}Due to Zeeman splitting in the external field, every Landau level splits into two separate levels for the different spins. It turns out that the Zeeman splitting is almost exactly the same as the splitting of the Landau levels. This leads to pairs of levels (with different $\nu$) with a very small spacing between the two levels and a spacing of approximately $\hbar\omega_c$ between the pairs.
In Figure 1 the density of states for free electrons in a magnetic field is shown.
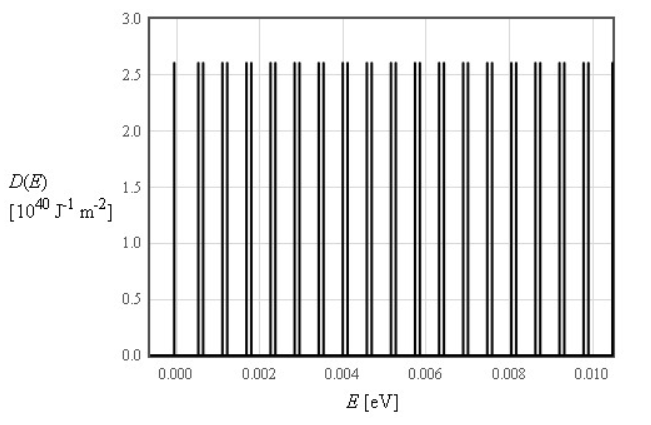 Figure 1: Denstiy of states in the 2D free electron model in the presence of a magnetic field.
Figure 1: Denstiy of states in the 2D free electron model in the presence of a magnetic field.In more detail, the density of states in 2D for free electrons is specified as:
\begin{equation*} D(E) = \frac{m \omega_c}{2 \pi \hbar} \sum_{\nu=0}^{\infty} \delta \left ( E - \hbar \omega_c \left(\nu + \frac{1}{2} \right) - \frac{g \mu_B}{2} B\right ) + \delta \left ( E - \hbar \omega_c \left(\nu + \frac{1}{2}\right) + \frac{g \mu_B}{2} B\right ) \end{equation*}How does the specific heat in the free electron model change when an magnetic field is applied?
As all thermodynamic properties in the free electron model show periodic behaviour in $1/B$ also the specific heat $c_V$ will show periodic behaviour when a magnetic field is applied
The reason for this is that the Landau levels move through the Fermi surface when changing the magnetic field. Whenever the Fermi energy is inside a Landau level, there is a high density of states at the Fermi energy, leading to a higher specific heat.
Why does the longitudinal resistivity $\boldsymbol{\rho_{xx}}$ go to zero in the Quantum Hall effect?
If you apply a magnetic field to a 2DEG, the electrons in the bulk regions perform circular motions. In the border regions of the sample, the electrons can’t perform full circular motions, because they get scattered back from the interface. These scattering events give these electrons a higher energy. The magnetic field forces scattered electrons to move in forward direction so that the current flows without resistivity in the edge channels. The energy-eigenvalues of the circular motion are the same as for the harmonic oscillator with the eigenfrequency $\omega_c$, where $\omega_c$ is the cyclotron frequency:
\begin{equation*} \omega_c = -\frac{e \cdot B_z}{m_{||}^*} \end{equation*}$m_{||}^*$ is the effective mass of the electrons parallel to the circular motion. Therefore the magnetic field causes a further quantization of the energy bands. The
resulting energy bands are called Landau-levels. If you solve the Schrödinger equation for free electrons in a magnetic field, you get the energy-eigenvalues of the Landau-levels:
\begin{equation*} E_{k,\nu} = \frac{\hbar^2 k_z^2}{2m^*} + \hbar \omega_c \left(\nu + \frac{1}{2}\right). \end{equation*}In this equation $\nu$ indicates the number of the Landau-level. The energy gap between two Landau-levels is $\hbar\omega_c$. Therefore the gap between the Landau-levels gets bigger when the magnetic field is increased. Figure 2 shows the Landau levels including the edge of the sample (a).
If the highest Landau level is far away from the Fermi-energy, then there are no states available for scattering (see Figure 2b) and the Quantum-Hall resistivity remains constant and the Shubnikov-de Haas-resistivity goes to zero. The reason for the latter is, that if a voltage is applied in one direction, one edge gets more populated than the other. This results in a net current flow. In that case the electron transport in the edge states is ballistic.
When you increase the magnetic field, the highest Landau-level gets near the Fermi-energy (see Figure 2c). In that case there are states available for scattering in the bulk regime and the resistivity increases. This scattering causes the peaks in the Shubnikov-de Haas oscillations and also the growth of the Quantum-Hall resistivity.
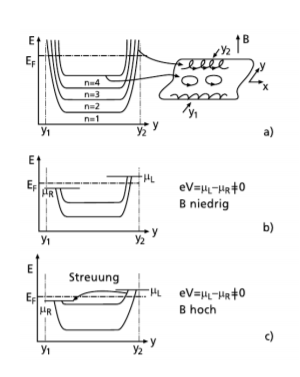 Figure 2: The resulting Landau levels after applying an external magnetic field (a). In (b) the highest Landau level is far away from the Fermi energy. Because the highest Landau level is filled, there are no unoccupied states available for electrons to scatter into. In (c) the highest Landau level is close to the Fermi energy. Scattering is possible.
Figure 2: The resulting Landau levels after applying an external magnetic field (a). In (b) the highest Landau level is far away from the Fermi energy. Because the highest Landau level is filled, there are no unoccupied states available for electrons to scatter into. In (c) the highest Landau level is close to the Fermi energy. Scattering is possible.Due to the external magnetic field the density of states gets split into Landau levels. These Landau levels are filled up until the Fermi energy. As long as the Fermi energy does not intersect with the highest Landau level, all possible states are filled, so an electron has no possible state to scatter into, hence the resistivity for $\rho_{xx}$ goes to $0$.
2. Quantum Hall Effect
The Quantum Hall effect is measured in samples where electrons are restricted to a two-dimensional plane. Often the electrons are confined to the interface between two materials.
- Describe the quantum Hall effect
- In a quantum Hall experiment, the magnetic field is held constant and a gate electrode is used to change the electron density. While the gate is changed, the conductivity is measured as in the Shubnikov-de Haas oscillations. Sketch the conductivity vs. electron density and explain why it has the form you have drawn?
- What other properties of a two dimensional electron gas will depend on the electron density?
Solution
Describe the quantum Hall effect
The quantum Hall effect is a quantum-mechanical version of the Hall effect, observed in two-dimensional electron systems subjected to low temperatures and strong magnetic fields, in which the Hall conductance $\sigma$ undergoes quantum Hall transitions to take on the quantized values.
The degeneracy of the Landau levels is given as:
\begin{equation}\label{eq:degeneracy_landau} D_L = \frac{2\pi e B_z}{\hbar} \end{equation}As $B$ increases, the spacing between the Landau levels also increases. All Landau levels below the Fermi energy are completely filled. If a Landau level crosses the Fermi energy it can only be partly filled.
When only completely filled Landau levels exist, an electron has no possible state to scatter into, hence it sees no resistance in the longitudinal direction.
The Hall resistivity $\rho_{xy}$ is known from the classical Hall effect to be
\begin{equation*} \rho_{xy} = -\frac{B_z}{ne}. \end{equation*}The $B$-field can be expressed from \eqref{eq:degeneracy_landau} as $B_z = D_Lh/e$ and the electron density must be equal to the number of occupied Landau levels $\nu$ times the degeneracy of the Landau levels, i.e. $n = \nu D_L$. For the Hall resistivity this means
\begin{equation*} \rho_{xy} = -\frac{h}{\nu e^2}. \end{equation*}The longitudinal resistivity $\rho_{xx}$ and Hall resistivity $\rho_{xy}$ are plotted as a function of $B$ in figure 3.
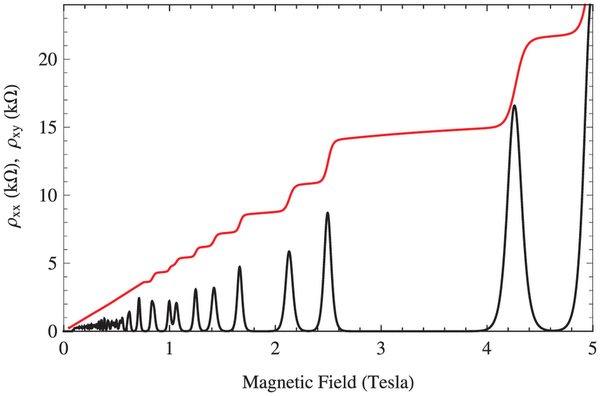 Figure 3: $\rho_{xx}$ and $\rho_{xy}$ as functions of the magnetic field $B$.
Figure 3: $\rho_{xx}$ and $\rho_{xy}$ as functions of the magnetic field $B$.
Drawn in red is $\rho_{xy}$, drawn in black is $\rho_{xx}$In a quantum Hall experiment, the magnetic field is held constant and a gate electrode is used to change the electron density. While the gate is changed, the conductivity is measured as in the Shubnikov-de Haas oscillations. Sketch the conductivity vs. electron density and explain why it has the form you have drawn?
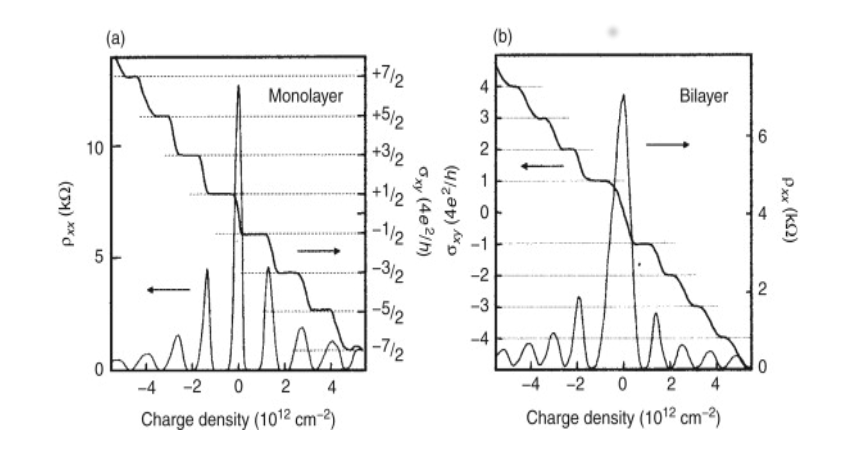 Figure 4: Resistivity and Hall conductivity vs. charge density in a two-dimensional electron gas.
Figure 4: Resistivity and Hall conductivity vs. charge density in a two-dimensional electron gas.What other properties of a two dimensional electron gas will depend on the electron density?
Almost all properties depend on the electron density, in particular all thermodynamic properties such as the specific heat etc.
3. Quantum Hall effect in a MOSFET
- What is the relationship between the cyclotron frequency and the magnetic field? (The frequency can be calculated with classical physics).
- The quantum Hall effect will only be observed if the energy splitting between the Landau levels is larger than thermal fluctuations. Derive a relation of the form $B/T > \ldots$ that tells us under which conditions the quantum Hall effect can be observed.
- The gate of the MOSFET can be used to change the two-dimensional electron density. What would happen to the Landau levels if the electron density were reduced?
- Explain what inversion in a MOSFET is and how it can be used to obtain a 2-D metal.
- Sketch the density of states for a 2-D metal in a magnetic field.
- Sketch the resistivity and the Hall resistivity as a function of the magnetic field.
- Why do the Shubnikov-de Hass oscillations disappear for low magnetic field?
Solution
What is the relationship between the cyclotron frequency and the magnetic field? (The frequency can be calculated with classical physics).
It can be calculated by setting the centrifugal force equal to the Lorentz force in the plane perpendicular to the field,
\begin{equation*} \frac{mv^2}{R} = qvB. \end{equation*}The frequency of the motion is then given by $\omega = v/R$, i.e.
\begin{equation*} \omega_c = \frac{qB}{m}. \end{equation*}In terms of the Bohr magneton
\begin{equation*} \mu_B = \frac{e\hbar}{2m} \end{equation*}this relation can also be written as
\begin{equation} \label{eq:omegac_b} \hbar\omega_c = 2\mu_BB. \end{equation}The quantum Hall effect will only be observed if the energy splitting between the Landau levels is larger than thermal fluctuations. Derive a relation of the form $\boldsymbol{B/T > \ldots}$ that tells us under which conditions the quantum Hall effect can be observed.
Effects of Landau levels are only observed when the mean thermal energy is smaller than the energy level separation
\begin{equation*} \hbar\omega_c \gg k_B T \end{equation*}meaning low temperatures and strong magnetic fields.
Using \eqref{eq:omegac_b} an expression for $B/T$ can be derived:
\begin{equation*} \frac{B}{T} \gg \frac{k_B}{2\mu_B}. \end{equation*}The gate of the MOSFET can be used to change the two-dimensional electron density. What would happen to the Landau levels if the electron density were reduced?
The number of completely filled Ladau levels is given as
\begin{equation*} \mathfrak{N} = \frac{n}{D_L} \end{equation*}with $n$ as the electron density and $D_L$ as the degeneracy of the Landau levels (in essence the spacing between landau levels), which is defined as:
\begin{equation*} D_L = \frac{m \omega_c}{\pi \hbar} \end{equation*}As the electron density is reduced, the landau levels get depopulated.
Explain what inversion in a MOSFET is and how it can be used to obtain a 2-D metal.
Consider an n-type MOSFET. When a voltage is applied to the gate the valence band edge is driven away from the Fermi level and holes from the body are driven away from the gate.
At higher voltage applied to the gate, both the conduction and valence band bend even further, until the conduction band edge is brought close to the Fermi level. This populates the surface with electrons from the conduction band in an inversion layer or n-channel at the interface between the p-region and the oxide. This channel extends between source and drain, creating a conducting channel. Current can flow through this channel if a voltage is applied between source and drain.
This behaviour is called inversion. Due to the high electron density in the inversion layer the channel behaves like a 2-D metal.
The electrons in the inversion layer are confined to the interface between oxide and semiconductor interface and thus occupy well defined energy levels. For thin-enough potential wells and temperatures not too high, only the lowest level is occupied, and so the motion of the electrons perpendicular to the interface can be ignored. However, the electron is free to move parallel to the interface, and so is quasi-two-dimensional.
Sketch the density of states for a 2-D metal in a magnetic field.
Details see question 1 a.
 Figure 5: Density of states for a 2-D metal in a magnetic field
Figure 5: Density of states for a 2-D metal in a magnetic fieldSketch the resistivity and the Hall resistivity as a function of the magnetic field.
Details see question 2 a.
 Figure 6: Resistivity and Hall resistivity as a function of the magnetic field
Figure 6: Resistivity and Hall resistivity as a function of the magnetic fieldWhy do the Shubnikov-de Hass oscillations disappear for low magnetic field?
For low magnetic fields the thermal oscillations of the electrons are much bigger than the spacing between the Landau levels, therefore at $B = 0$ the density of states is continuous. As the magnetic field increases the Landau levels start defining the populated states. Only if the magnetic field is large compared to the thermal fluctuations the density of states reaches $0$ for certain energies and the Shubnikov-de Haas oscillations start to appear. This relation between the magnetic field and the thermal oscillation can be expressed in terms of $\hbar \omega_c \gg k_BT$:
\begin{equation*} \frac{B}{T} \gg \frac{k_B}{2 \mu_B} \end{equation*}
4. Shubnikov-de Haas oscillations
- What are Shubnikov-de Haas oscillations? Why do they occur?
- What other quantities exhibit oscillations as the magnetic field is varied?
- How can the oscillations be used to experimentally determine the Fermi surface of a metal?
Solution
What are Shubnikov-de Haas oscillations? Why do they occur?
The Shubnikov-de Haas oscillations are oscillations of the resistivity parallel to the electric field in a 2DEG (2-dimensional electron gas) in an applied magnetic field. Therefore they are related to the Quantum-Hall effect. The Shubnikov-de Haas oscillations have a $1/B$-periodicity.
The reason for the oscillating behavior is, that the Landau levels move through the Fermi surface while varying the magnetic field, because their spacing depends on the field. When the Fermi energy is inside a Landau level, there are lots of states for the electrons at the Fermi energy to scatter into, which leads to a large resistivity. If the Fermi surface is between two Landau levels, then we would expect insulating behavior, but at the edges of the sample there are states, which can carry a current (see question 1 c). Since then there are no states to scatter into, this current is dissipationless (in the limit of $E_F$ far away from a Landau level), leading to lower resistivity (even zero for higher fields).
What other quantities exhibit oscillations as the magnetic field is varied?
- Fermi energy: When a Landau-level crosses the Fermi-energy as a result of an increasing magnetic field it gets depopulated. That means, that the electrons jump into the lower lying Landau-levels. As soon as the highest Landau-level is completely unoccupied the Fermi-energy is in the next highest Landau-Level. This level has a lower energy than the now unoccupied level and therefore the Fermi-energy is lower than before.
- Internal Energy
- Magnetization (de Haas-van Alphen oscillations)
- All other quantities that depend on the density of states, e.g. Entropy, Helmholtz free energy, Pressure, Bulk modulus. The number of states is constant but when a Landau level crosses the Fermi energy and gets depopulated, the density of states changes. This causes oscillations in all quantities that depend on the density of states.
All these quantities have a $1/B$-periodicity like the Shubnikov-de Haas oscillations. In the high field limit, when there is only one occupied Landau-level, these quantities all grow linearly.
How can the oscillations be used to experimentally determine the Fermi surface of a metal?
See question 4 in Electrons b.