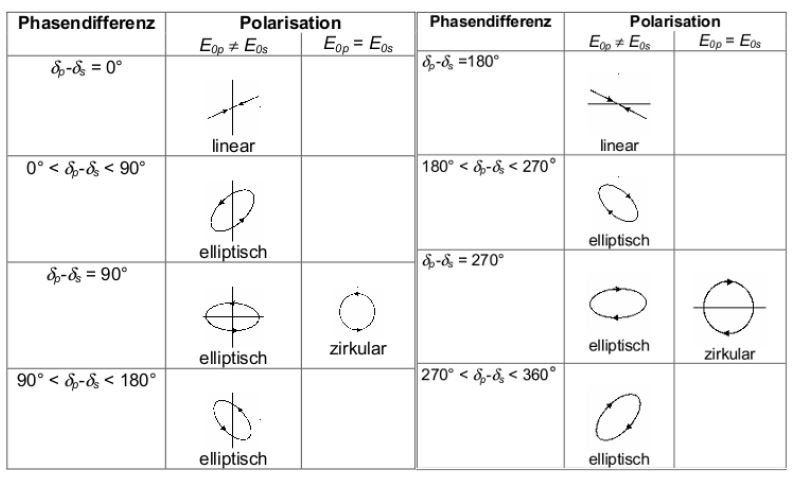
Abb 1: Mögliche Polarisationszustände des Lichts, ausgedrückt durch die Differenz der Phase sowie der relativen Amplituden [1].
Ellipsometrie - Grundlagen
Ellipsometrie basiert auf der änderung des Polarisationszustands von Licht bei der Reflexion an Grenzflächen und in Medien. Grundlage der theoretischen Beschreibung ist dabei immer die Maxwell'sche Theorie.
Es genügt den Lichtstrahl als ebene monochromatische Welle zu nähern. Somit läßt sich das elektrische Feld schreiben als
$\vec{k}$ = $\frac{2\pi}{\lambda}$ ist dabei der Wellenvektor und $\omega$ die Frequenz. Zur Beschreibung der Richtung der Polarisation wählen wir eine Basis relativ zur Einfallsebene. Die Einfallsebene ergibt sich aus der Ausbreitungsrichtung des einfallenden Lichts sowie dem Lot auf der reflektierenden Grenzfläche (oder der Richtung des reflektierten Lichts). Wir können dann $\vec{E}$ in eine senkrechte ($E_s$) und parallele ($E_p$) Komponente relativ zur Einfallsebene zerlegen. Das hat den Vorteil, daß diese Vektoren bei Reflexion des Lichtstrahls ihre Richtung relativ zur Einfallsebene nicht ändern. Die p- und die s- Richtung bilden daher eine geeignete zweidimensionale orthogonale Basis zur Beschreibung der Polarisationsrichtung. Berücksichtigt man noch eine mögliche Verschiebung der Phasen zwischen den beiden Komponenten, läßt sich $\vec{E}$ durch einen komplexen Vektor, dem sogenannten Jones-Vektor, ausdrücken:
\begin{equation} \vec{E}= \begin{pmatrix} |E_p| e^{i \delta_p}\\ |E_s| e^{i \delta_s}\\ \end{pmatrix} = \begin{pmatrix} E_p\\ E_s\\ \end{pmatrix} \end{equation}Die unterschiedlichen Polarisationszustände ergeben sich also aus Betrag und Phasenverschiebung der Komponenten. Die Polarisation des Lichts ist

Abb 1: Mögliche Polarisationszustände des Lichts, ausgedrückt durch die Differenz der Phase sowie der relativen Amplituden [1].
Wird Licht an einer Oberfläche reflektiert, ändert sich im allgemeinen der Polarisationszustand. Die Meßung dieser änderung erlaubt Rückschlüße auf die Beschaffenheit des Materials und ist Gegenstand der Ellipsometrie. Im oben eingeführten Jones-Formalismus läßt sich die änderung des Polarisationszustands elegant beschreiben, da sich für rein p- oder rein s-polarisiertes Licht die Polarisation bei Reflexion nicht ändert. Diese Richtungen stellen somit eine orthogonale Basis von Eigenvektoren bezüglich der Reflexion an isotropen Medien dar. Für die einfallende und die reflektierte Lichtwelle gilt [1]:
\begin{equation} \vec{E}_i= \begin{pmatrix} |E_{ip}| e^{i \delta_{ip}}\\ |E_{is}| e^{i \delta_{is}}\\ \end{pmatrix}, \qquad \vec{E}_r= \begin{pmatrix} |E_{rp}| e^{i \delta_{rp}}\\ |E_{rs}| e^{i \delta_{rs}}\\ \end{pmatrix} \end{equation}Hier beschreibt $E_i$ die einfallende und $E_r$ die reflektierte Welle. Die Reflexion an einem Medium wird allgemein durch entsprechende Reflexionskoeffizienten $r_p$ und $r_s$ beschrieben. Diese sind komplexe Zahlen um die änderung des elektrischen Feldes bezüglich Phase und Amplitude richtig wieder zu geben und sind definiert als das Verhältnis der einfallenden zur auslaufenden Welle:
\begin{equation} r_p = \frac{|E_{rp}|}{|E_{ip}|} e^{i(\delta_{rp}-\delta_{ip})}, \qquad r_s = \frac{|E_{rs}|}{|E_{is}|} e^{i(\delta_{rs}-\delta_{is})} \end{equation}Berechnet man hieraus das Verhältnis $\frac{r_p}{r_s}$, erhält man die sogenannte $\textbf{Ellipsometergleichung}$
\begin{equation} \label{eq1} \tan(\Phi) \cdot e^{i\Delta} = \frac{r_p}{r_s} \end{equation}mit
\begin{equation} \tan(\Phi) = \frac{\frac{|E_{rp}|}{|E_{ip}|}}{\frac{|E_{rs}|}{|E_{is}|}} \quad \text{und}\quad \Delta = (\delta_{rp}-\delta_{ip})-(\delta_{rs}-\delta_{is}) \end{equation}Durch Meßen der Winkel $\Phi$ und $\Delta$ erhält man so Information über die optischen Eigenschaften des reflektierenden Systems, da diese in den Reflexionskoeffizienten enthalten sind. Um die Ellipsometerwinkel $\Phi$ und $\Delta$ zu erhalten, muß man sowohl die änderung der relativen Phasenlage der s- und p- Komponente meßen, als auch die änderung der Verhältniße der beiden Amplituden.
Ein besonders einfaches Verfahren dazu stellt die Nullellipsometrie dar. Dabei wird der Polarisationszustand des einfallenden Lichts so eingestellt, daß das reflektierte Licht linear polarisiert ist, was sich besonders einfach nachweisen läßt durch Auslöschung der reflektierten Intensität mittels eines gekreuzten Polarisators, dem Analysators (A). Der Winkel des Analysators $\alpha_A$ ergibt direkt den Ellipsometerwinkel $\Phi$, da er nur vom Verhältnis der s- und p-Komponenten abhängt. Die im allgemeinen elliptische Polarisation des einfallenden Lichts wird geformt durch einen Polarisator (P) und einem Kompensator (K), wobei sich aus der Winkelstellung $\alpha_P$ des Polarisators relativ zum Kompensator direkt der Phasenwinkel $\Delta$ ergibt. Besitzt der Kompensator eine Neigung von $\alpha_K$ = $\pm$45°, so kann man zeigen daß gilt:
\begin{equation} \mp \tan(\alpha_A)e^{i(2\alpha_P \pm \pi/2)} = \frac{r_p}{r_s} \end{equation}Ein Vergleich mit der Ellipsometergleichung \ref{eq1} zeigt, daß
\begin{equation} \Phi = |\alpha_A| \quad \text{und} \quad \Delta = 2\alpha_P \pm \pi/2 \end{equation}Man kann also $\Delta$ und $\Phi$ druch Ablesen der eingestellten Winkel an Analysator und Polarisator bestimmen.Ein großer Vorteil der Ellipsometrie im Vergleich zu anderen Verfahren ist, daß nur die Winkel der Polarisation in die Ellipsometergleichung eingehen während absolute Intensitäten keine Rolle spielen. So können eventuelle Intensitätßchwankungen die Meßergebniße kaum verfälschen [1].
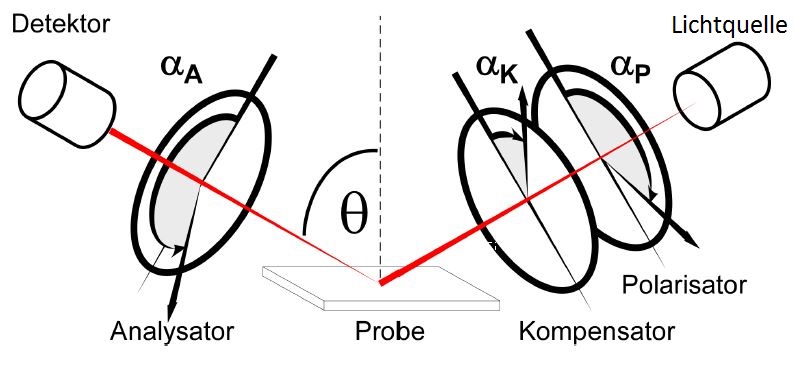
Abb 2: Schematischer Aufbau eines Ellipsometers [1]
In Abbildung 2 ist der prinzipelle Aufbau des Ellipsometers dargestellt. Als Quelle dient eine durchstimmbare Lichtquelle. Der linear polarisierte Lichtstrahl wird durch ein $\lambda/4$-Plättchen in linear polarisiertes Licht verwandelt, bevor er auf den Polarisator trifft. Im einzelnen durchläuft der Lichtstrahl dann folgende Bauteile:
Bestimmung dielektrische Funktion
Die oben bestimmten Reflexionskoeffizienten sind über die Fresnel’schen Gleichungen mit den komplexen dielektrische funktionen
$\epsilon_i$ und $\epsilon_t$ von der Probe und Umgebung verknüpft:
mit $\theta_i$ ist gleich dem Einfallswinkel und $\theta_t$ ist gleich dem Transmißionswinkel. Der daraus bestimmbare komplexe Brechnungsindex besteht aus den Realteil $n$ (reeler Brechungsindex) und den Imaginärteil $K$ (Extinktionskoeffizient) [2]
\begin{equation} \sqrt{\epsilon(\omega)} = n(\omega) + i K(\omega) \end{equation}