Standard mathematical functions abs(x), acos(x), asin(x), cos(x), exp(x), pi = 3.141592653589793, pow(x,y) = xy, round(x), sin(x), sqrt(x) can be used in the form. In addition the Heaviside step function H(x) can be used. H(x<0) = 0, H(x=0) = 0.5, H(x>0) = 1. Multiplication must be specified with a '*' symbol, 3*cos(x) not 3cos(x). Powers are specified with the 'pow' function: x² is pow(x,2) not x^2.
Some tunnel potentials that can be pasted into the form are given below.
Calculating the current
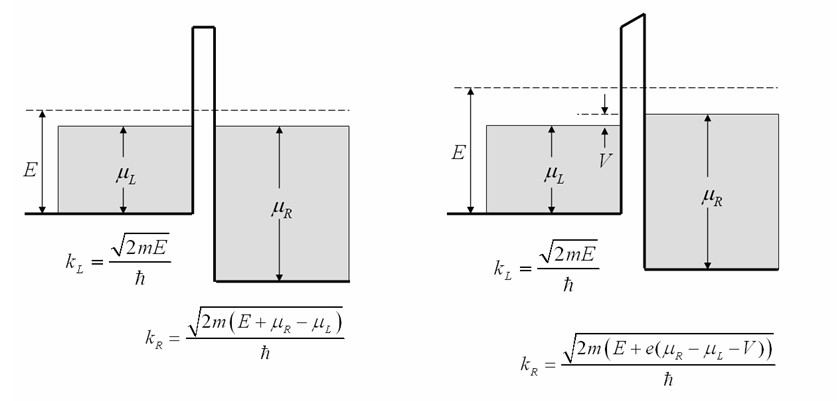
In three dimensions, electrons can tunnel through a barrier at any angle. Most of the contribution to the tunnel current will come from electrons that tunnel perpendicular to the barrier. Those electrons that don't tunnel perpendicular to the barrier have a longer tunnel path and therefore the transmission probability for those electrons will be low. Here we only include those electrons in the calculation with $k$ vectors that are perpendicular to the tunnel barrier. This results in a one-dimensional problem which simplifies the calculation significantly. In a one-dimensional system, when the energy of an electron state is known, the wavefunction everywhere can be calculated by integrating the Schrödinger equation numerically.

The figure above shows the potential at zero bias on the left and finite bias on the right. The Schrödinger equation is solved for an electron of energy $E$ moving in a potential given by thick black line. All of the states shaded gray are filled at low tempertures. If the metals on the two sides of the tunnel barrier are different, the $k$ values of an electron of energy $E$ will be different on the left and on the right.