PHY.K02UF Molecular and Solid State Physics
|
| ||||
PHY.K02UF Molecular and Solid State Physics | ||||
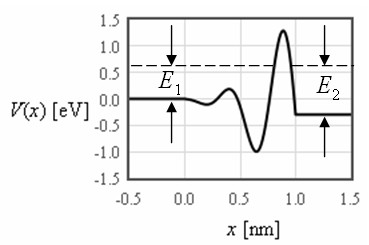
In quantum mechanics, there is some probability that a particle of mass m will tunnel through a potential barrier even if the energy of the particle is less than the energy of the barrier. During a direct tunneling process, the energy of the electron remains contant. The form below calculates the transmission coefficient for tunneling. The shape of the tunnel barrier can be arbitrarily defined in the interval between x = 0 and x = a. The potential is assumed to be constant to the left of the tunnel barrier at the value V(x=0) and constant to the right of the barrier at the value V(x=a).
Standard mathematical functions abs(x), acos(x), asin(x), cos(x), exp(x), pi = 3.141592653589793, pow(x,y) = xy, round(x), sin(x), sqrt(x) can be used in the form. In addition the Heaviside step function H(x) can be used. H(x<0) = 0, H(x=0) = 0.5, H(x>0) = 1. Multiplication must be specified with a '*' symbol, 3*cos(x) not 3cos(x). Powers are specified with the 'pow' function: x² is pow(x,2) not x^2.
Some tunnel potentials that can be loaded into the form are given below.
Calculating the transmission coefficient
Consider a particle that approaches a potential barrier from the left with a energy E indicated by the dashed line in the figure above. In quantum mechanics, the motion of the particle is described by a complex wave function that is a solution to the Schrödinger equation. This wave will be partially transmitted through the barrier and partially reflected.
To the left of the barrier, the wave function that describes the incident wave coming from the left is ΨI(x,t) and the reflected wave moving to the left has a wave function described by ΨR(x,t).
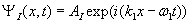
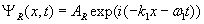
To the right of the barrier, the transmitted wave function has the form,
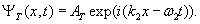
The relationship between the energy E, wave number k, and angular frequency ω can be found by substituting the wavefunctions into the Schrödinger equation.
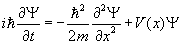
To the left of the barrier,
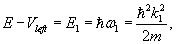
and to the right of the barrier,

For a tunnel barrier defined bewteen x = 0 and x = a, the wave function can be determined by specifying the wave function and its derivative at x = a,
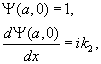
and integrating the Schrödinger equation numerically to x = 0. The wave function and its derivative must match to the solutions for x < 0.
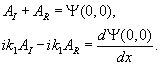
Solving for the complex amplitudes of the incident and reflected waves,

The reflection coefficient is,

The waves that are not reflected are transmitted so the transmission coefficient is T = 1 - R.