The differential equation that describes the motion of the of a damped driven oscillator is,

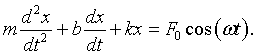
Here m is the mass, b is the damping constant, k is the spring constant, and F₀cos(ωt) is the driving force.

It is common to use complex numbers to solve this problem. Consider the complex differential equation,

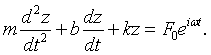
The driving function F₀e^iωt describes a point that moves in the complex plane in a circle of radius F₀ at a constant angular velocity of ω. The real part of this motion is the original driving force, F₀cos(ωt). Since the equation for z is a linear differential equation, we know that the steady state solution will have the form z = Ae^iωt. Substituting this solution into the differential equation results in the following characteristic equation.

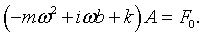
The factor in parenthesis can be written in polar form,

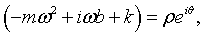
where

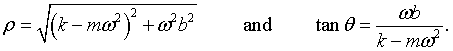
The amplitude of the solution is therefore,

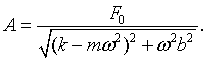
Just like F₀e^iωt, Ae^iωt is a point that moves in a circle in the complex plane. It moves at the same frequency as the driving force but it has a different amplitude and phase. The response lags behind the drive by a phase θ.

Simulation of the motion in the complex plane.

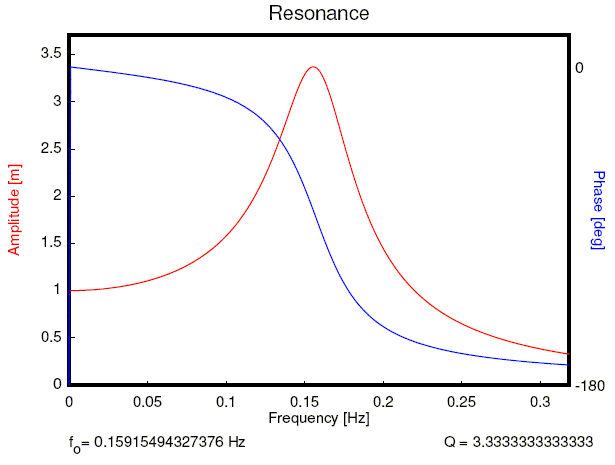
This plot shows the amplitude of the oscillations as a function of frequency and the corresponding phase shift. The following form will generate a resonance curve like the one above.

m [kg] = b [N s/m] = k [N/m] F0 [N]