PHY.K02UF Molecular and Solid State Physics
|
| ||||
PHY.K02UF Molecular and Solid State Physics | ||||
The closest packing of spheres in two dimensions has hexagonal symmetry where every sphere has six nearest neighbors. Hexagonal close-packing corresponds to a ABAB stacking of such planes.
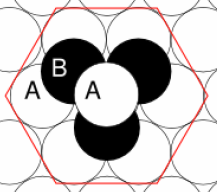
Each atom has twelve nearest neighbors in hcp. In the ideal structure, the distance between the planes is 1.633$a$, where $a$ is the distance between the atoms. For some materials that are commonly considered hcp, the distance bewteen the planes deviates from the ideal structure. Beryllium, Magnesium and Titanium form hcp.
Crystal structure: HCP
Bravais lattice: hexagonal close-packed
Space group: 194 (P63/mmc), Strukturbericht: A3, Pearson symbol: hP2
Point group: 6/mmm (D6h) 1 six-fold rotation axis C6, 6 two-fold rotations axes C2, 1 horizontal mirror plane $\sigma$h, 6 vertical mirror plane $\sigma$v, 1 centre of inversion $i$
Lattice constants: Be: $a=0.2290$ nm, $\frac{c}{a}=1.567$; Mg: $a=0.3210$ nm, $\frac{c}{a}=1.624$; Ti: $a=0.2950$ nm, $\frac{c}{a}=1.588$.
Atomic density: $n_{\text{atoms}}= \sqrt{2}/a^3$
The lattice parameters of the conventional unit cell are:
\[ \begin{equation} a = b; c = 1.633 a \text{ (ideal)}, \hspace{0.5cm} \alpha = 90^{\circ} , \,\beta = 90^{\circ} ,\,\gamma = 120^{\circ} . \end{equation} \]The primitive cell of the hexagonal closed packed (hcp) lattice is given by the three lattice vectors:
$\vec{a}_1=\frac{a}{2}\hat{x}+\frac{-\sqrt{3}a}{2}\hat{y}$, $\vec{a}_2=\frac{a}{2}\hat{x}+\frac{\sqrt{3}a}{2}\hat{y}$, $\vec{a}_3=c\hat{z}$.
with two atoms in the cell located at the fractional coordinates:
$\vec{B}_1=(0,0,0)$, $\vec{B}_2=(0.33,0.66,0.5)$.
The asymmetric unit contains one atom at fractional coordinate (0,0,0). The positions of the other atoms can be determined by applying the symmetries of the space group.
Space group: 194 (P63/mmc)
24 symmetry operations:
Matrix Rotation-part type Axis direction Screw/glide component Origin shift x,y,z 1 - - - x-y,x,z+1/2 6^1 [0,0,1] 0,0,1/2 0,0,0 -y,x-y,z 3^1 [0,0,1] 0,0,0 0,0,0 -x,-y,z+1/2 2 [0,0,1] 0,0,1/2 0,0,0 -x+y,-x,z 3^-1 [0,0,1] 0,0,0 0,0,0 y,-x+y,z+1/2 6^-1 [0,0,1] 0,0,1/2 0,0,0 -y,-x,-z+1/2 2 [-1,1,0] 0,0,0 0,0,1/4 x-y,-y,-z 2 [1,0,0] 0,0,0 0,0,0 x,x-y,-z+1/2 2 [2,1,0] 0,0,0 0,0,1/4 y,x,-z 2 [1,1,0] 0,0,0 0,0,0 -x+y,y,-z+1/2 2 [1,2,0] 0,0,0 0,0,1/4 -x,-x+y,-z 2 [0,1,0] 0,0,0 0,0,0 -x,-y,-z -1 - - 0,0,0 -x+y,-x,-z-1/2 -6^1 [0,0,1] 0,0,0 0,0,-1/4 y,-x+y,-z -3^1 [0,0,1] 0,0,0 0,0,0 x,y,-z-1/2 -2 [0,0,1] 0,0,0 0,0,-1/4 x-y,x,-z -3^-1 [0,0,1] 0,0,0 0,0,0 -y,x-y,-z-1/2 -6^-1 [0,0,1] 0,0,0 0,0,-1/4 y,x,z-1/2 -2 [-1,1,0] 0,0,-1/2 0,0,0 -x+y,y,z -2 [1,0,0] 0,0,0 0,0,0 -x,-x+y,z-1/2 -2 [2,1,0] 0,0,-1/2 0,0,0 -y,-x,z -2 [1,1,0] 0,0,0 0,0,0 x-y,-y,z-1/2 -2 [1,2,0] 0,0,-1/2 0,0,0 x,x-y,z -2 [0,1,0] 0,0,0 0,0,0