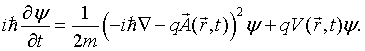The Hamiltonian of a charged particle in a magnetic field is,

Here A is the vector potential. When a magnetic field is present, the kinetic momentum mv is no longer the conjugate variable to position. The conjugate variable to position is p = mv + qA. In this section, this Hamiltonian will be derived starting from Newton's law.

The force on a charged particle is,

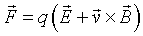
The force is a function of both the position and the velocity of the particle. To describe the motion of the charged particle quantum mechanically, one needs to construct the Hamiltonian. However, to find the conjugate variable the Lagrangian needs to be constructed first. The force is related to the Lagrangian by the Euler-Lagrange equation,

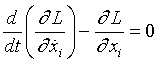
When the Lagrangian is substituted into the Euler-Lagrange equation, the result is Newton's law for the force in question. The Lagrangian is constructed from the force 'by inspection'. This means that we guess a Lagrangian and substitute it into the Euler-Lagrange equation. If the trial Lagrangian produces the correct form for Newton's law, that that is the Lagrangian we are seeking.

We assert that the appropriate Lagrangian is,

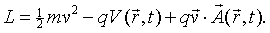
By substituting this Lagrangian into the Euler-Lagrange equations, we will show that it describes the motion of a particle of mass m and charge q in the presence of electric and magnetic fields described by the scalar potential V and vector potential A.

The Euler-Lagrange equation corresponding to the x coordinate is,

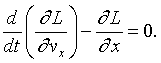
Here

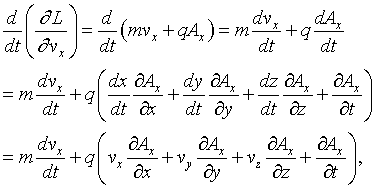
and

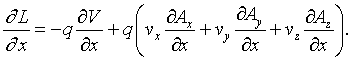
Combing these results yields,

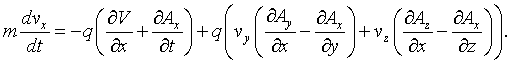
This is the x component of Newton's law,

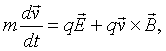
where,

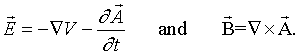
The y and z components of Newton's law can similarly be determined from the Euler-Lagrange equations.

By definition, the conjugate variable to the position x is,

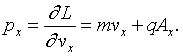
The mv_x component of the conjugate variable is called the kinetic momentum and the qA_x component of the conjugate is called the field momentum. The notation can be confusing here. The variable p_x is the conjugate variable to the x-coordinate, not the kinetic momentum.

A Legendre transformation is used to obtain the Hamiltonian from the Lagrangian,

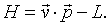
Using the expression for the Lagrangian from above,

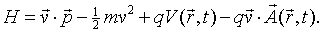
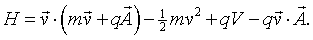
Thus the Hamiltonian for a charged particle in an electric and magnetic field is,

$$H=\frac{\left(\vec{p}-q\vec{A}\right)^2}{2m}+qV.$$

The quantity p is the conjugate variable to position. It includes a kinetic momentum term and a field momentum term. So far, this derivation has been entirely classical. (Hamilton died long before anyone thought about quantum mechanics.) To make the transition to quantum mechanics we replace p by 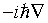. The Schrödinger equation for a charged particle in a magnetic field is,