|
| |
Superconductivity
About one third of all metals undergo an electronic phase transition to a superconducting state at low temperatures. Superconductors have zero dc resistivity and display perfect diamagnetism. Above the critical temperature $T_c$, the electrons are fermions but below the critical temperature the electrons form Cooper pairs. The Cooper-pairs consist of two electrons and have spin 0 so they are bosons. The bosons condense into a single quantum state at low temperature.
Brief History
- 1911: Superconductivity was discovered by Heike Kamerlingh Onnes. It was immediately recognized that superconductivity would be useful for constructing magnets. It was observed that superconductivity could be suppressed by the application of a critical magnetic field $H_c$. It was also observed that superconducting wires could carry current up to a critical current density $J_c$ before the wire would return to the normal resistive state.
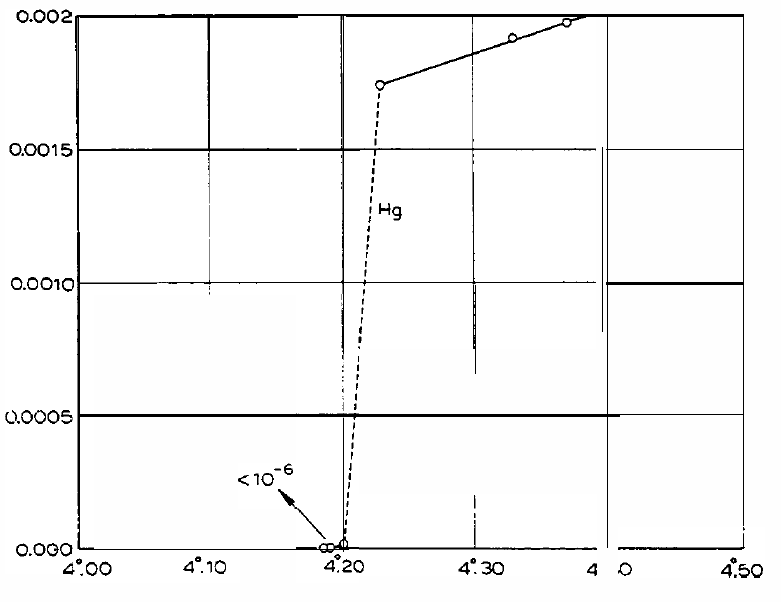
The resistivity of the first known superconductor, Hg, as a function of temperature.
Source: Heike Kamerlingh Onnes, Nobel Lecture 1913
- 1933: Meissner and Ochsenfeld showed that superconductors are perfect diamagnets with a diamagnetic susceptibility of $\chi_m = -1$. This demonstrates that superconductivity is more than just perfect conductivity. If a very good conductor is placed in a constant magnetic field, the field lines will penetrate through the conductor. As a good conductor is cooled down, the conductivity increases but the field continues to pass through the conductor. If a constant magnetic field is applied to a superconductor in the high-temperature normal state, the field will penetrate through the conductor. As the superconductor is cooled through the critical temperature, the magnetic field is expelled from the interior of the superconductor. This is known as the Meissner effect.

Source: Wikimedia Commons
- 1935: Fritz and Heinz London proposed phenomenological equations to describe the electromagnetic properties of superconductors. The first London equation is,
$$\frac{d\vec{j}_s}{dt} = \frac{n_se^2}{m_e}\vec{E}.$$
Here $\vec{j}_s$ is the current density of the superconducting electrons, $n_s$ is the density of superconducting electrons, $\vec{E}$ is the electric field, $e$ is the electrons charge and $m_e$ is the electron mass. Just below the critical temperature, the superconducting electrons coexist with electrons in the metal that have not condensed into the superconducting state. The density of superconducting electrons grows from zero at $T_c$ until all of the valence electrons of the metal condense into the superconducting state at low temperature. The second London equation is,
$$\nabla \times \vec{j}_s = - \frac{n_se^2}{m_e}\vec{B},$$
where $\vec{B}$ is the magnetic field. The equation was just postulated by the London brothers because they observed that by assuming this was true, it results in the Meissner effect. The second London equation can be combined with Ampere's law to show that magnetic fields decay exponentially at the surface of a superconductor with a decay length called the penetration depth,
$$\lambda = \sqrt{\frac{m_e}{\mu_0n_se^2}}.$$
The penetration depth is typically between 10 nm and a few microns.
- 1950: Ginzbuurg and Landau developed a phenomenological theory of superconductivity based on Landau's theory of second order phase transitions. The free energy of the superconductor was expressed in terms of a complex order parameter $\psi$. The expression for the free energy is,
$$f=f_n+\alpha |\psi|^2 +\frac{\beta}{2}|\psi|^4 +\frac{1}{2m_{cp}}\left|\left(-i\hbar\nabla-2e\vec{A}\right)\psi\right|^2+\frac{\mu_0H^2}{2}.$$
Here $f_n$ is the free energy in the normal state, $m_{cp}$ is the mass of a Cooper pair, $|\psi|^2$ is proportional to the concentration of electrons in the superconducting state. The concentration of electrons in the superconducting state increases continuously from zero at $T_c$ to a finite value for $T < T_c$. $\alpha$ and $\beta$ are constants that describe how the free energy depends on the order parameter near the phase transition. These constants are described in Landau's theory of second order phase transitions. The third term on the right describes the energy density due to the kinetic energy of the superconducting electrons and the last term is the magnetic energy density. Ginzburg-Landau theory introduces a new characteristic length called the coherence length $\xi= \frac{\hbar^2 |\psi_0|^2}{2m_{cp}\mu_0H_c^2}$. The theory is related to the theory of superfluid 4He. Helium-4 atoms are bosons and it was understood that at low temperatures they form a Bose-Eistein condensate. It was known at the time that quantized vortices could exist in superfluid helium.
- 1957: Abrikosov used Ginzburg-Landau theory to show that for magnetic fields above a critical field, in superconductors where the $\frac{\lambda}{\xi} > \frac{1}{\sqrt{2}}$ the magnetic field will enter the superconductor as vortices. The core of the vortex has a radius of approximately the coherence length and the superconducting order parameter is suppressed in the core. The magnetic flux passes through this core and decays exponentially with the penetration depth to zero in the surrounding superconductor. Each vortex contains one flux quantum $\Phi_0 = \frac{h}{2e} \approx 2.0678\times 10^{-15}\,\text{Wb}$ of magnetic flux. Superconductors are classified as type I if $\frac{\lambda}{\xi} < \frac{1}{\sqrt{2}}$. Magnetic fields are expelled out of a type I superconductors up to a critical field $H_c$ where superconductivity is suppressed. Below $H_c$, type I superconductors are perfect diamagnets. Type II superconductors, $\frac{\lambda}{\xi} > \frac{1}{\sqrt{2}}$, expell magnetic fields up up a lower critical field $H_{c1}$. Above $H_{c1}$ vortices enter the superconductor but superconductivity is not suppressed until an upper critical field $H_{c2}$. Type II superconductors are important for high-field magnets and superconducting cables that carry large currents. Ginzburg-Landau theory relates the critical fields to the characteristic lengths. The lower critical field is,
$$H_{c1} = \frac{\Phi_0}{4\pi\mu_0\lambda^2}.$$
The vortices have an outer radius of about $\lambda$. $H_{c1}$ is approximately the field where the vortices start to overlap. The critical field is,
$$H_{c} = \frac{\Phi_0}{2\sqrt{2}\pi\mu_0\lambda\xi}.$$
If $\sqrt{2}\lambda < \xi$, then $H_c < H_{c1}$ and superconductivity is suppressed before the vorticies enter. This is a type I superconductor. For a type II superconductor, nothing dramatic happens at $H_c$. Superconductivity is suppressed at the upper critical field,
$$H_{c2} = \frac{\Phi_0}{2\pi\mu_0\xi^2}$$
This is approximately the field where the cores of the vortices overlap. The critical current density is,
$$J_c = \frac{\Phi_0}{3\sqrt{3}\pi\mu_0\lambda^2\xi}$$
- 1957: Bardeen, Cooper, and Schrieffer published the first microscopic theory of superconductivity.
$$n_s\Delta \approx n_sk_BT_c \approx \frac{\mu_0 H_c^2}{2} \approx \frac{n_sm_ev^2}{2} \approx \frac{m_eJ_c^2}{2n_se^2}$$
- Superconductivity W
- Meissner effect W
- BCS theory W
- London equations W
- Ginzburg Landau theory W
- Josephson effects W
- SQUID W
Reading
Kittel chapter 10: Superconductivity
Resources
- A good book on superconductivity is Introduction to Superconductivity by Michael Tinkham.
- Superconductors.org
- Investigations into the Properties of Substances at Low Temperatures, which Have Led, amongst Other Things, to the Preparation of Liquid Helium, Heike Kamerlingh Onnes, Nobel Prize 1913 (pdf).
- Electron-Phonon Interactions and Superconductivity, John Bardeen, Nobel Prize 1972 (pdf).
- Microscopic Quantum Interference Effects in the Theory of Superconductivity, Leon N. Cooper, Nobel Prize 1972 (pdf).
- Macroscopic Quantum Phenomena from Pairing in Superconductors, Robert Schrieffer, Nobel Prize 1972 (pdf).
- Electron Tunneling and Superconductivity, Ivar Giaever, Nobel Prize 1973 (pdf).
- The Discovery of Tunnelling Supercurrents, Brian D. Josephson, Nobel Prize 1973 (pdf).
- Perovskite-Type Oxides – The New Approach to High-Tc Superconductivity, J. Georg Bednorz and K. Alex Müller, Nobel Prize 1987 (pdf).
- Type II Superconductors and the Vortex Lattice, Alexei A. Abrikosov, Nobel Prize 2003 (pdf) (video).
- On Superconductivity and Superfluidity, Vitaly L. Ginzburg, Nobel Prize 2003 (pdf) (video).
- Critical temperatures of the elements
|

