2-D Schrödinger equation
3-D Schrödinger equation
Eigenfunction solutions


Energy eigenvalues
Density of states
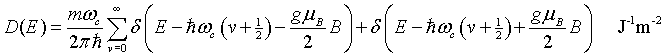



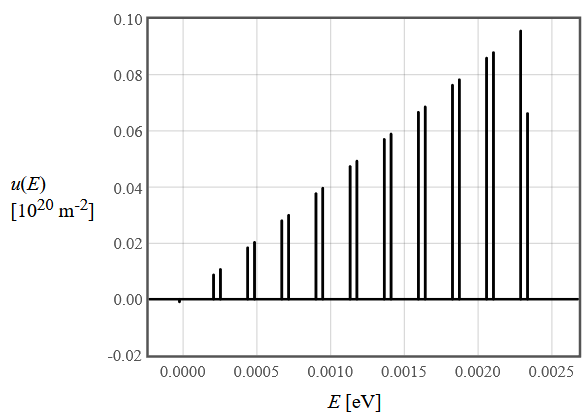
Energy spectral density
at zero temperature

Fermi energy EF


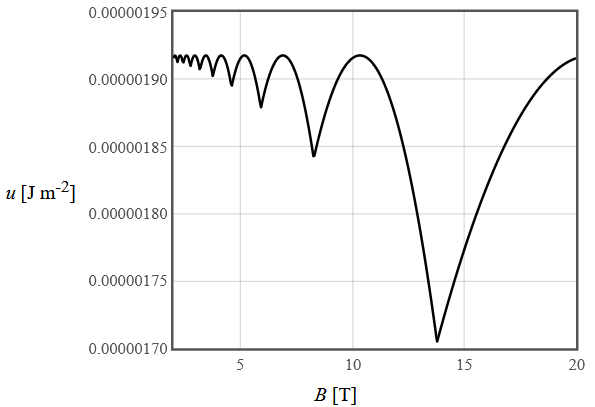
Internal energy
at zero temperature

Magnetization
at zero temperature


2-D Schrödinger equation | 3-D Schrödinger equation | ||||||
Eigenfunction solutions |
|
| |||||
Energy eigenvalues | $$E=\hbar \omega_c\left( \nu+ \frac{1}{2}\right) \pm \frac{g\mu_B}{2}B_z$$ $$E=\hbar \omega_c\left( \nu+ \frac{1}{2}\pm \frac{g}{4}\right) $$ $$\nu = 0,1,2,\cdots\qquad\omega_c=\frac{|eB_z|}{m}$$ | $$E=\hbar \omega_c\left( \nu+ \frac{1}{2}\right) + \frac{\hbar^2}{2m} k_{z}^2 \pm \frac{g\mu_B}{2}B_z$$ $$E=\hbar \omega_c\left( \nu+ \frac{1}{2}\pm \frac{g}{4}\right) + \frac{\hbar^2}{2m} k_{z}^2 $$ $$\nu = 0,1,2,\cdots\qquad\omega_c=\frac{|eB_z|}{m}$$ | |||||
Density of states |
|
| |||||
Energy spectral density |
|
| |||||
Fermi energy EF |
|
| |||||
Internal energy |
|
| |||||
Magnetization |
|
|