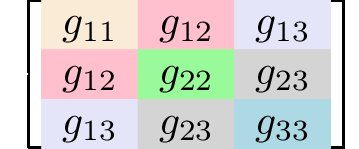
A tensor is called symmetric if all of its elements, whose indices are permutations of one another, are the same. Generally, rank 2 tensors (matrices) have nine independent elements,
$$\left[\begin{matrix} g_{11} & g_{12} & g_{13} \\ g_{21} & g_{22} & g_{23} \\ g_{31} & g_{32} & g_{33} \\ \end{matrix}\right].$$However, symmetric rank 2 tensors have only six independent elements
$$g_{11}\\g_{22}\\g_{33}\\g_{12} = g_{21}\\ g_{13} = g_{31}\\g_{23} = g_{32}.$$
Elements with the same background color have the same value. Examples of symmetric rank 2 tensors are the electric susceptibility and the magnetic susceptibility,
$$\chi^E_{ij} = \frac{\partial P_i}{\partial E_j} =-\frac{\partial ^2G}{\partial E_i\partial E_j} = \frac{\partial P_j}{\partial E_i} = \chi^E_{ji},$$ $$\chi^M_{ij} = \frac{\partial M_i}{\partial H_j} =-\frac{\partial ^2G}{\partial H_i\partial H_j} = \frac{\partial M_j}{\partial H_i} = \chi^M_{ji}.$$The elements of these matrices are the second derivatives of the Gibbs free energy and $\chi_{ij}=\chi_{ji}$ because the order in which the differentiation is taken does not matter.
A rank 3 tensor has 3 × 3 × 3 = 27 independent elements but a symmetric rank 3 tensor only has 10 independent elements because for a symmetric tensor, $$g_{111}\\g_{222}\\g_{333}\\ g_{112} = g_{121} = g_{211}\\ g_{122} = g_{212} = g_{221}\\ g_{113} = g_{131} = g_{311}\\ g_{133} = g_{313} = g_{331}\\ g_{223} = g_{232} = g_{322}\\ g_{233} = g_{323} = g_{332}\\ g_{123} = g_{132} = g_{213}= g_{231}= g_{312}= g_{321}\\ $$

An example of a symmetric rank 3 tensor is how the electric susceptibility depends on electric field,
$$\frac{\chi^E_{ij}}{\partial E_k} =-\frac{\partial ^3G}{\partial E_i\partial E_j\partial E_k} .$$Some rank 3 tensors are only symmetric in two indices $g_{ijk}=g_{ikj}$. When this happens there are 18 independent elements,
$$g_{111}\\g_{222}\\g_{333}\\g_{122}\\g_{133}\\g_{211}\\g_{233}\\g_{311}\\g_{322}\\ g_{112} = g_{121}\\ g_{113} = g_{131}\\ g_{123} = g_{132}\\ g_{212} = g_{221}\\ g_{213}= g_{231}\\ g_{223} = g_{232}\\ g_{312}= g_{321}\\ g_{313} = g_{331}\\ g_{323} = g_{332}\\ $$A rank 4 tensor has 3 × 3 × 3 × 3 = 81 independent elements but a symmetric rank 4 tensor only has 15 independent elements because for a symmetric tensor, $$g_{1111}\\g_{2222}\\g_{3333}\\ g_{1112} = g_{1121} = g_{1211}= g_{2111}\\ g_{1222} = g_{2122} = g_{2212}= g_{2221}\\ g_{1113} = g_{1131} = g_{1311}= g_{3111}\\ g_{1333} = g_{3133} = g_{3313}= g_{3331}\\ g_{2223} = g_{2232} = g_{2322}= g_{3222}\\ g_{2333} = g_{3233} = g_{3323}= g_{3332}\\ g_{1122} = g_{1212} = g_{1221}= g_{2112} = g_{2121} = g_{2211}\\ g_{1133} = g_{1313} = g_{1331}= g_{3113} = g_{3131} = g_{3311}\\ g_{2233} = g_{2323} = g_{2332}= g_{3223} = g_{3232} = g_{3322}\\ g_{1123} = g_{1132} = g_{1213}= g_{1312} = g_{1231}= g_{1321} = g_{2113}= g_{3112}= g_{2131}= g_{3121}= g_{2311}= g_{3211}\\ g_{2213} = g_{2231} = g_{2123}= g_{2321} = g_{2132}= g_{2312} = g_{1223}= g_{3221}= g_{1232}= g_{3212}= g_{1322}= g_{3122}\\ g_{3321} = g_{3312} = g_{3231}= g_{3132} = g_{3213}= g_{3123} = g_{2331}= g_{1332}= g_{2313}= g_{1323}= g_{2133}= g_{1233}\\ $$

Many properties are symmetric in two indices. The Voigt notation collects pairs of indices as follows:
$11 \rightarrow 1 \\ 22 \rightarrow 2 \\ 33 \rightarrow 3 \\ 23 = 32 \rightarrow 4 \\ 13 = 31 \rightarrow 5 \\ 12 = 21 \rightarrow 6 $
Or written in matrix form
$\left[\begin{matrix} g_{11} & g_{12} & g_{13} \\ g_{21} & g_{22} & g_{23} \\ g_{31} & g_{32} & g_{33} \\ \end{matrix}\right] \rightarrow \left[\begin{matrix} g_{1} & g_{6} & g_{5} \\ g_{6} & g_{2} & g_{4} \\ g_{5} & g_{4} & g_{3} \\ \end{matrix}\right] \rightarrow \left[\begin{matrix} g_{1} & g_{2} & g_{3} & g_{4} & g_{5} & g_{6} \end{matrix}\right] $
Whenever this notation is used, it implies a symmetry in the reduced indices.