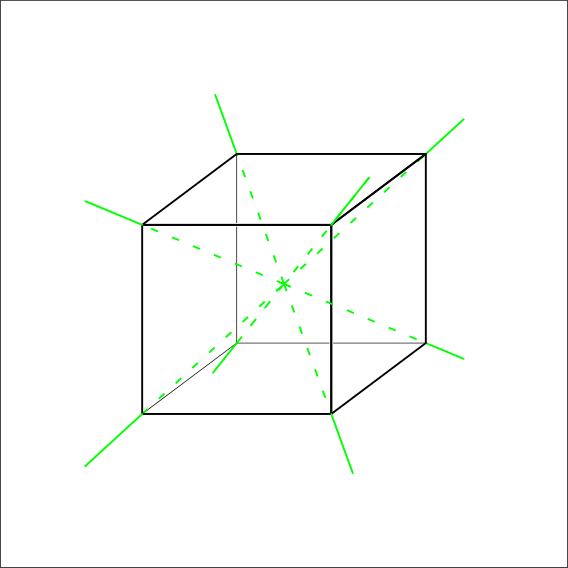
Does rotation around all four body diagonals have 3-fold symmetry?
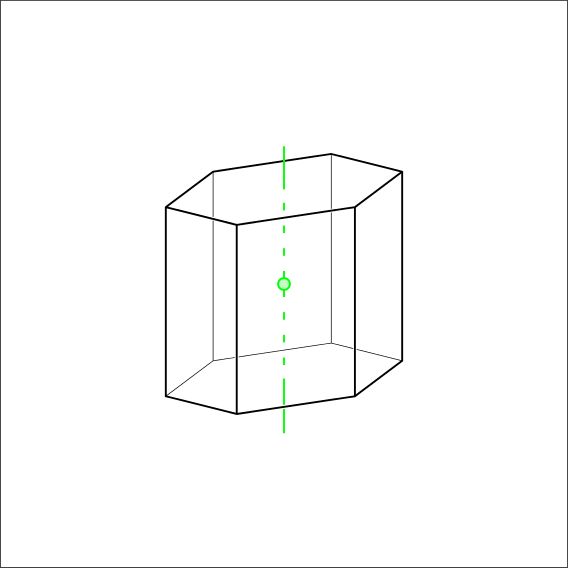
Is there a 6-fold symmetry or 6 Rotoinversion?
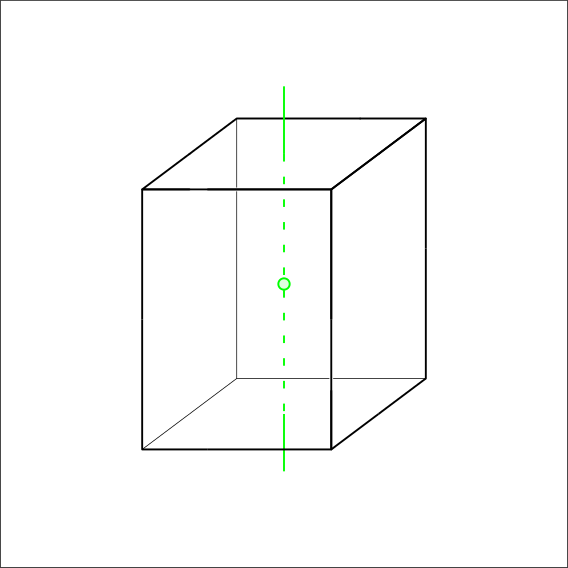
Is there a 4-fold symmetry or 4 Rotoinversion?
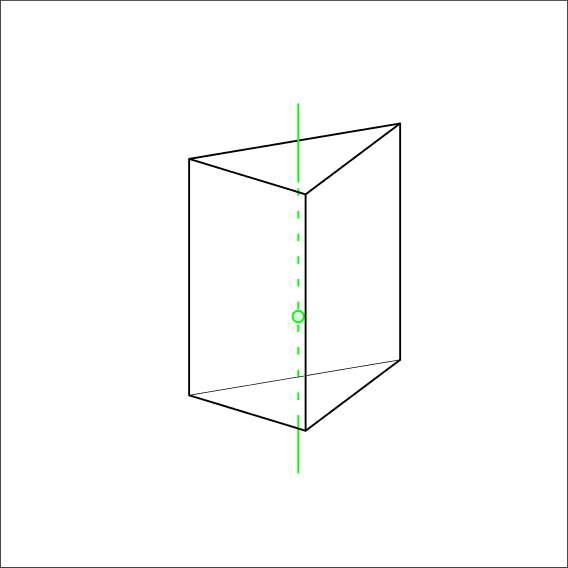
Is there a 3-fold symmetry or 3 Rotoinversion?
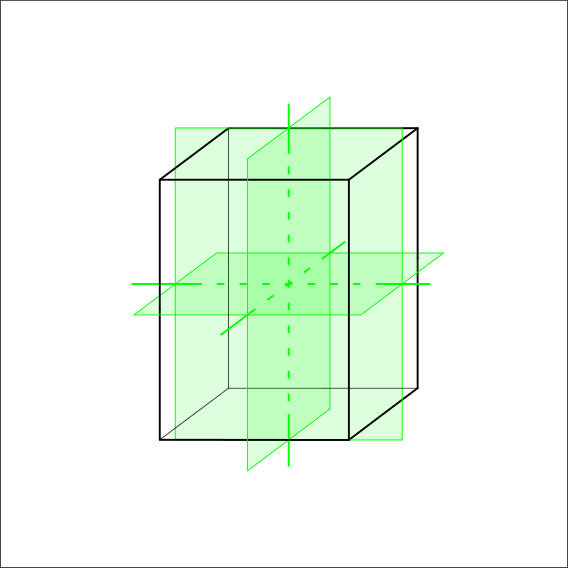
Does the object have three 2-fold symmetry axis and/or mirror planes that are perpendicular to each other?
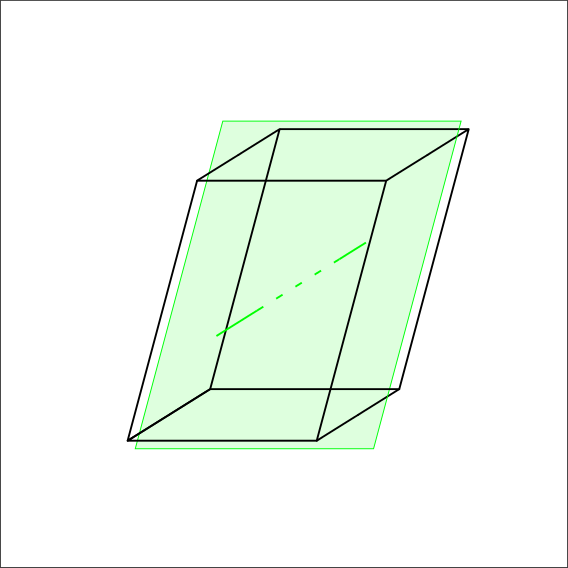
Is there a 2-fold symmetry axis and/or mirror plane?
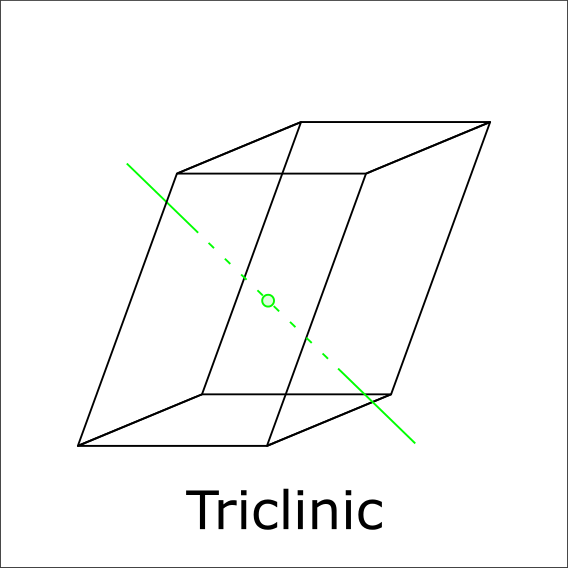
Is there a 1-fold symmetry or 1 rotoinversion?
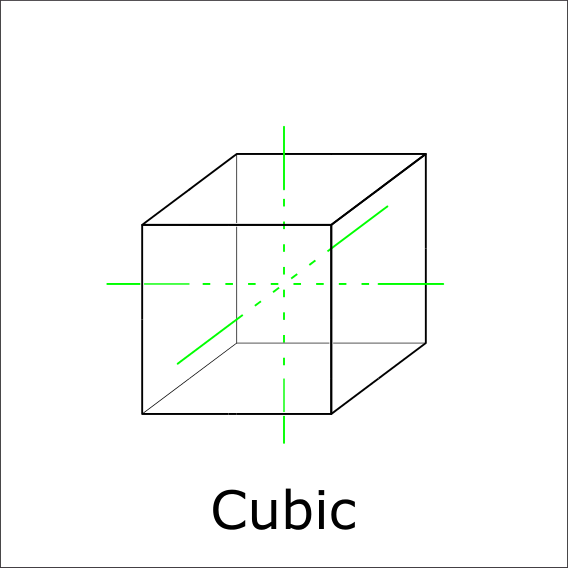
Are there three 4-fold rotations through the center?
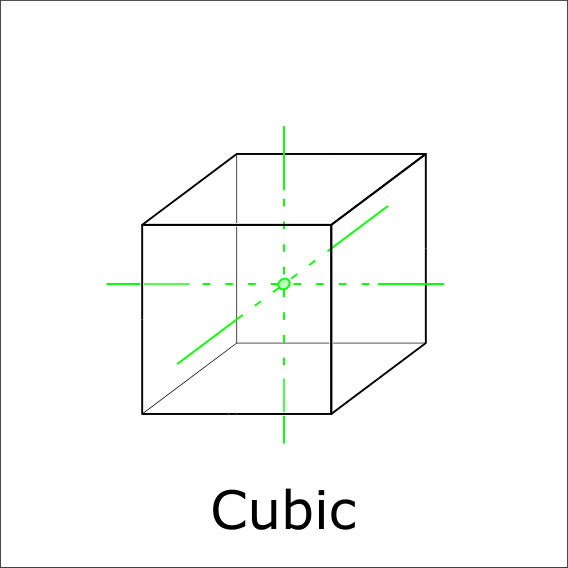
Are there three 4-fold rotoinversions through the center?
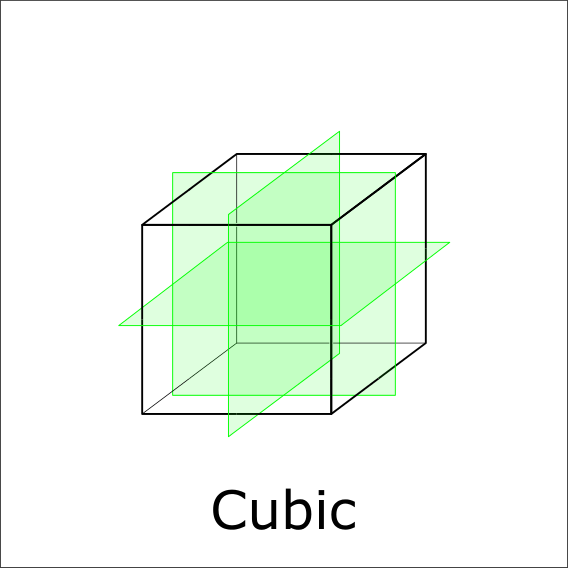
Is there a mirror plane perpendicular to the 4-fold axis?

Is there a mirrorplane perpendicular to a 4-fold axis?
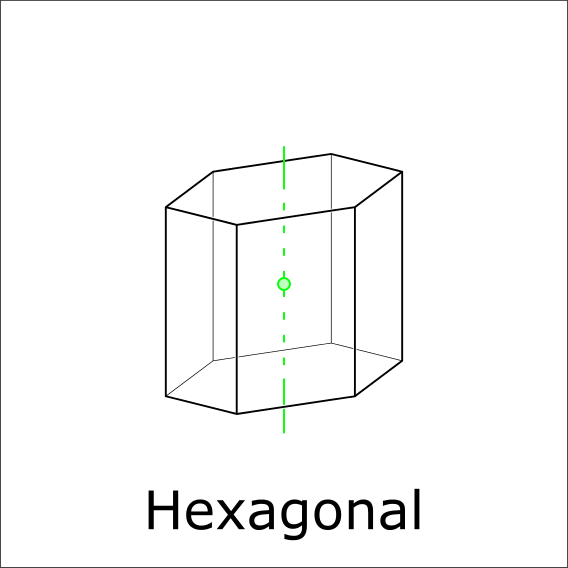
Is there a 6-fold rotoinversion?

Is there a mirror plane perpendicular to the 6-fold rotational axis?
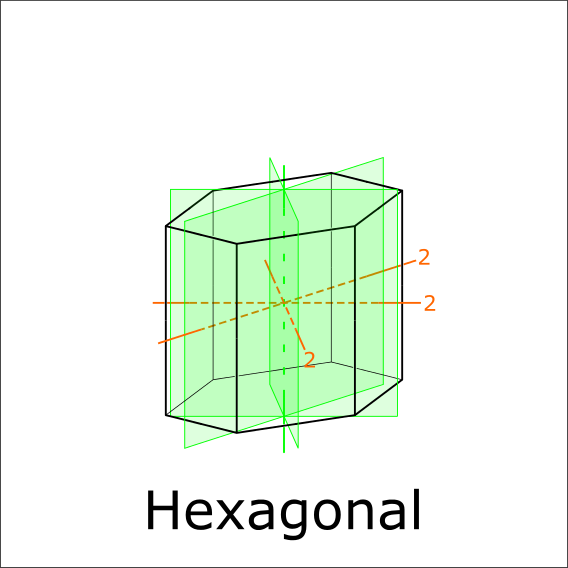
Are there mirror planes or 2-fold symmetries?
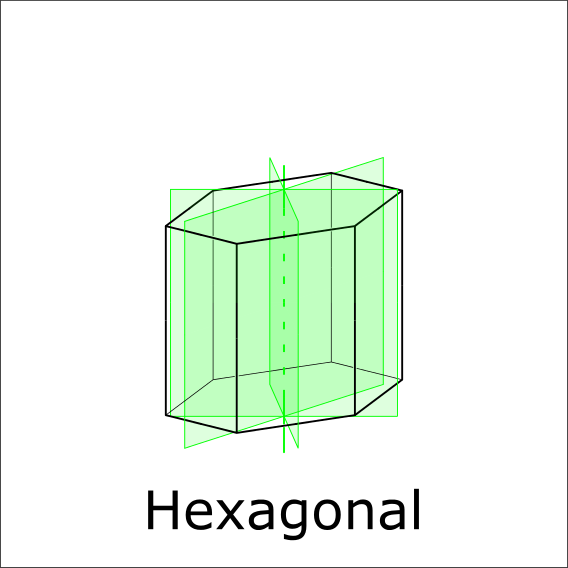
Mirror planes or 180° rotations?
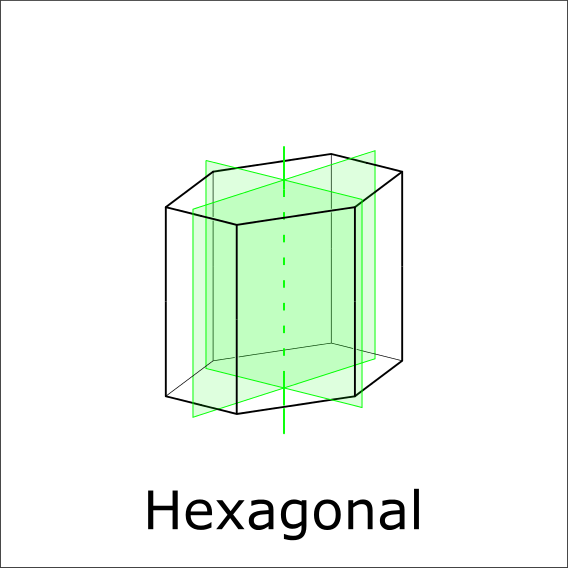
Additional mirror planes parallel to the 6-fold axis?
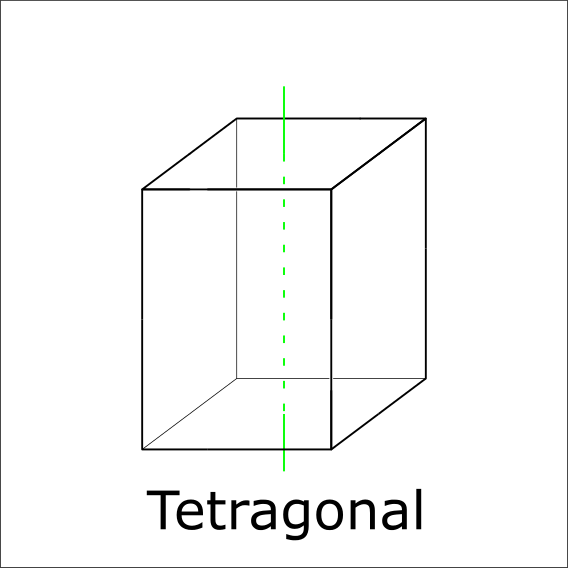
Is there a 4-fold symmetry axis?
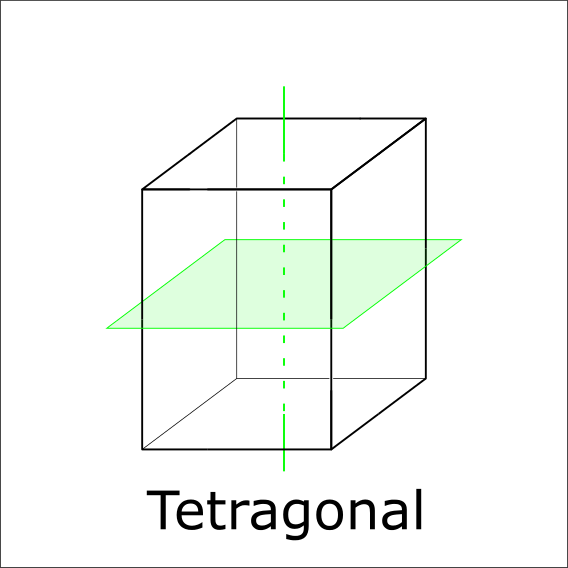
Is there a mirror plane perpendicular to the 4-fold axis?
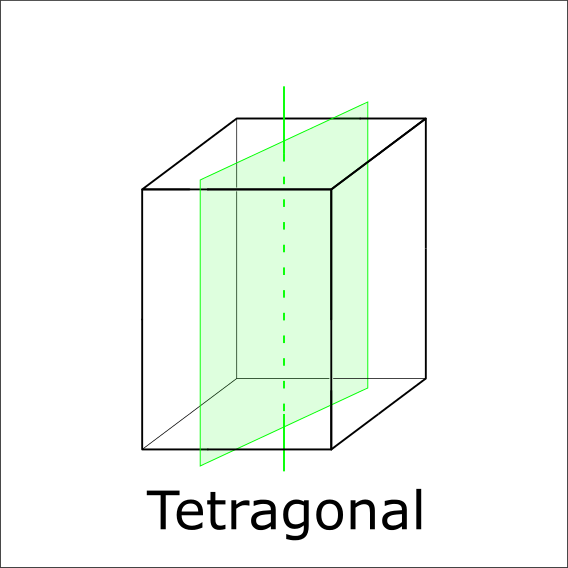
Is there a mirror plane paralell to the 4-fold axis?

Are there two 2-fold rotational axis perpendicular to the 4-fold axis?
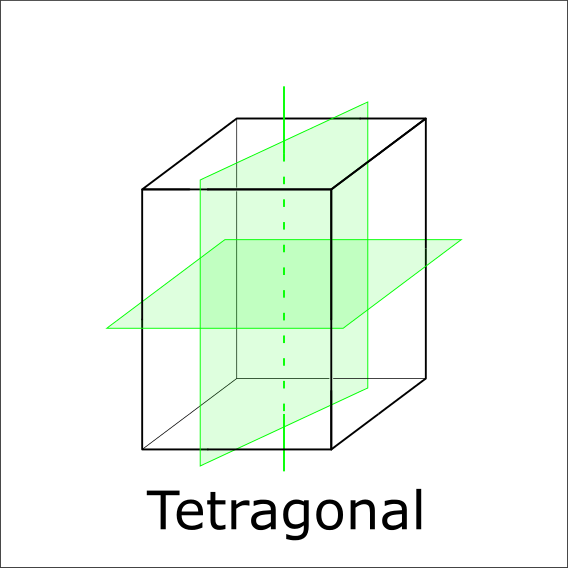
Any additional mirror planes parallel to the 4-fold axis?
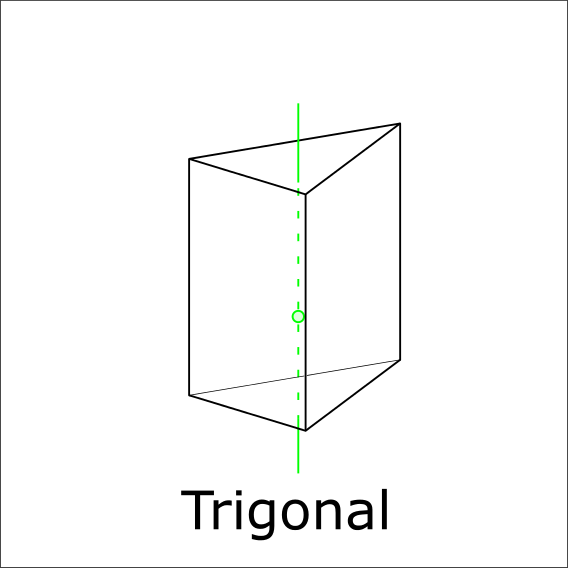
Is there 3 rotoinversion?
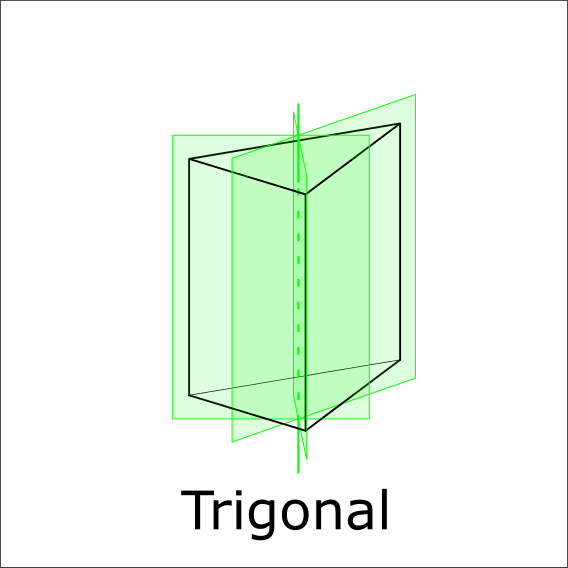
Are there three mirror planes paralell to the 3-fold axis?
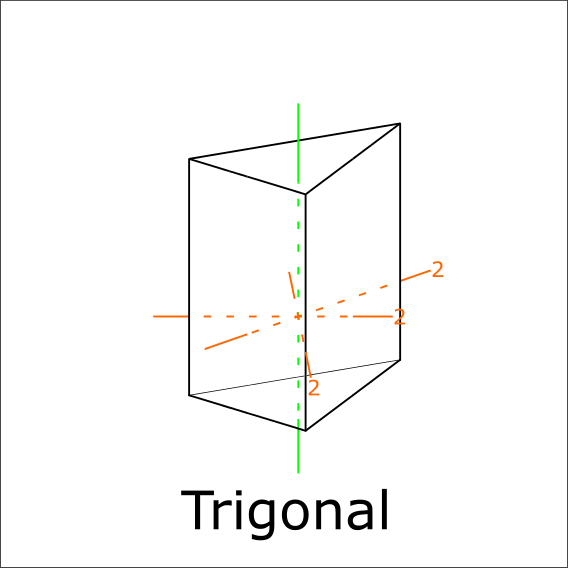
Are there three mirror planes perpendicular to the 3-fold axis?
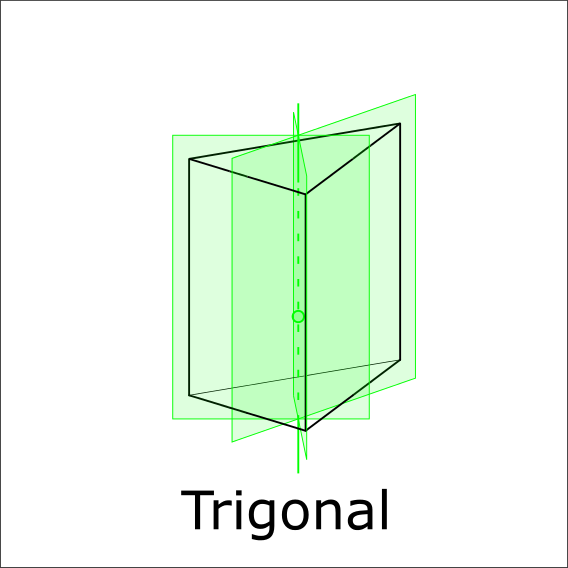
Are there three mirror planes paralell to the 3 rotoinversion axis?
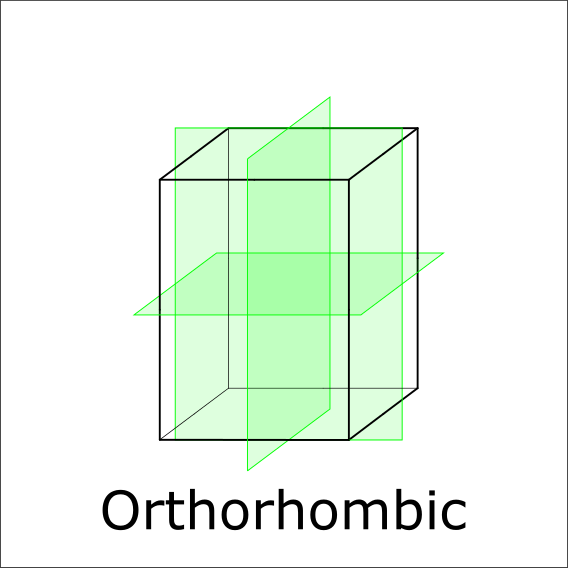
Are there three perpendicular mirror planes?
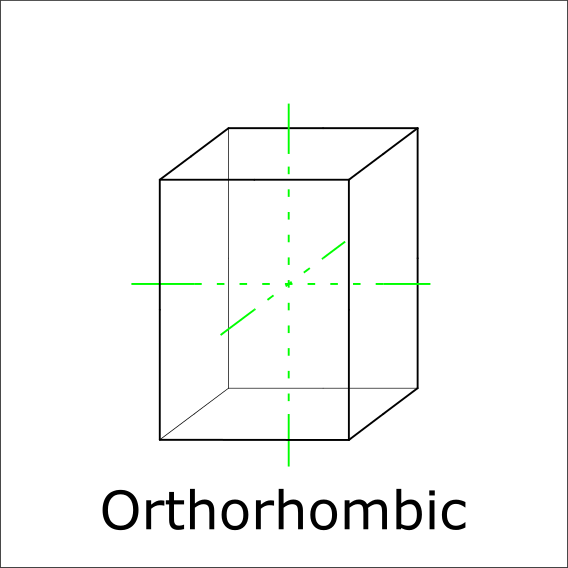
Are there three perpendicular 2-fold axis?
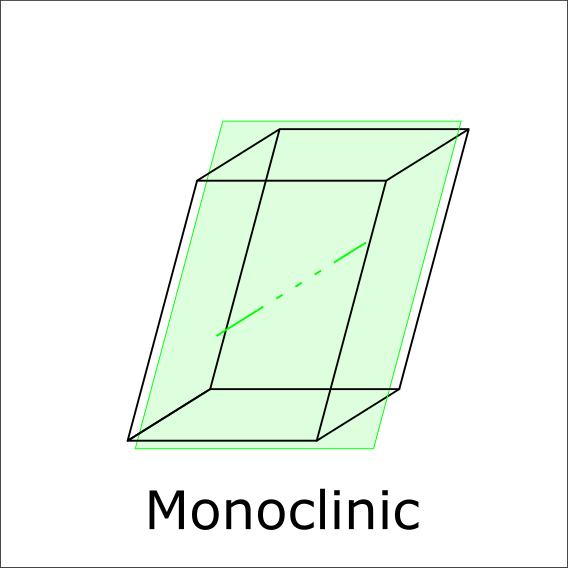
Is there a perpendicular mirrorplane to the 2-fold axis?
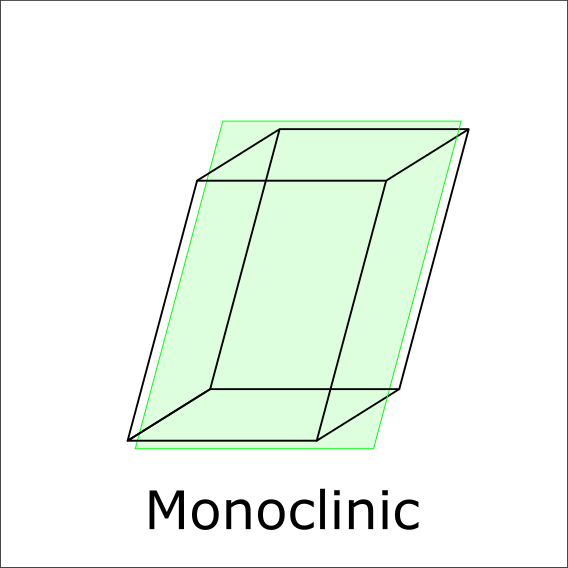
Is there a mirror plane?

Is there a 1-fold symmetry?
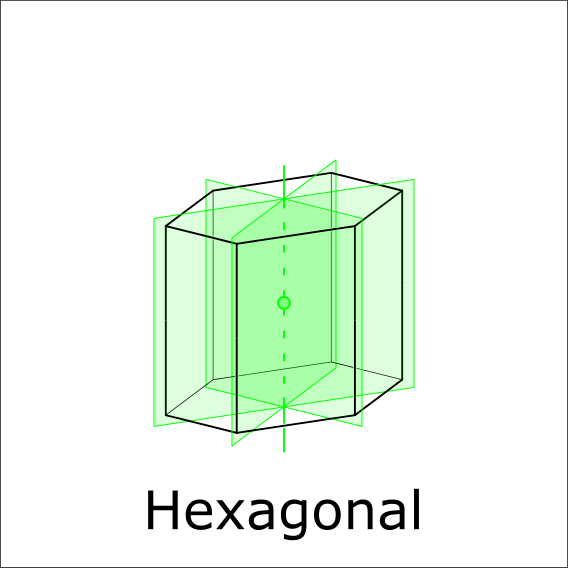
Are there mirror planes parallel to the 6 rotoinversion axis which are 120° apart?
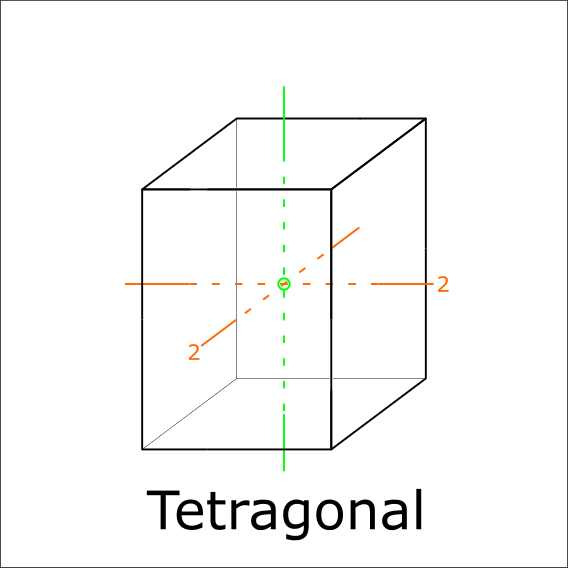
Are there two 2-fold rotations perpendicular to the 4-rotoinversion axis?
































