PHY.K02UF Molecular and Solid State Physics
|
| ||||
PHY.K02UF Molecular and Solid State Physics | ||||
Silicon is an indirect bandgap semiconductor.
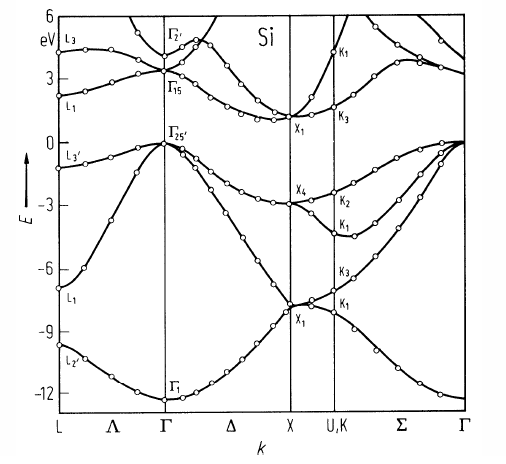
Source: O. Madelung, U. Rössler, M. Schulz (ed.)
SpringerMaterials
Silicon (Si), band structure
Landolt-Börnstein - Group III Condensed Matter 41A1b
(Group IV Elements, IV-IV and III-V Compounds. Part b - Electronic, Transport, Optical and Other Properties)
http://materials.springer.com/lb/docs/sm_lbs_978-3-540-31356-4_432
10.1007/10832182_432 (Springer-Verlag Berlin Heidelberg ©2002)
Accessed: 14-01-2016
The six 6 conduction band minima can be approximated by the paraboloids,
\[ \begin{equation} E_{c100}=E_g+\frac{\hbar^2}{2m_l}\left(k_x-\frac{1.7\pi}{a}\right)^2+\frac{\hbar^2}{2m_t}k_y^2+\frac{\hbar^2}{2m_t}k_z^2, \end{equation} \] \[ \begin{equation} E_{c\overline{1}00}=E_g+\frac{\hbar^2}{2m_l}\left(k_x+\frac{1.7\pi}{a}\right)^2+\frac{\hbar^2}{2m_t}k_y^2+\frac{\hbar^2}{2m_t}k_z^2, \end{equation} \] \[ \begin{equation} E_{c010}=E_g+\frac{\hbar^2}{2m_t}k_x^2+\frac{\hbar^2}{2m_l}\left(k_y-\frac{1.7\pi}{a}\right)^2+\frac{\hbar^2}{2m_t}k_z^2, \end{equation} \] \[ \begin{equation} E_{c0\overline{1}0}=E_g+\frac{\hbar^2}{2m_t}k_x^2+\frac{\hbar^2}{2m_l}\left(k_y+\frac{1.7\pi}{a}\right)^2+\frac{\hbar^2}{2m_t}k_z^2, \end{equation} \] \[ \begin{equation} E_{c001}=E_g+\frac{\hbar^2}{2m_t}k_x^2+\frac{\hbar^2}{2m_t}k_y^2+\frac{\hbar^2}{2m_l}\left(k_z-\frac{1.7\pi}{a}\right)^2, \end{equation} \] \[ \begin{equation} E_{c00\overline{1}}=E_g+\frac{\hbar^2}{2m_t}k_x^2+\frac{\hbar^2}{2m_t}k_y^2+\frac{\hbar^2}{2m_l}\left(k_z+\frac{1.7\pi}{a}\right)^2. \end{equation} \]Here $a = 0.543$ nm is the lattice constant, $m_t = 0.19m_e$ is the transverse electron effective mass, $m_l = 0.98m_e$ is the longitudinal electron effective mass, and $m_e = 9.11\times 10^{-31}$ kg is the mass of an electron.
The valence bands consist of a light hole band, a heavy hole band, and a split-off band. All three bands have a maximum at $k=0$. The light hole band and the heavy hole band are degenerate at $k=0$ while the energy of the split-off band is $E_{so}$ lower at $k=0$. The dispersion for the light holes and the heavy holes are given approximately by, [Askerov]
\[ \begin{equation} E_{v,lh}=-\frac{\hbar^2}{2m_{e}}\left(4.1k^2-\sqrt{1.21k^4+4.1(k_x^2k_y^2+k_x^2k_z^2+k_y^2k_z^2)}\right), \end{equation} \]and
\[ \begin{equation} E_{v,hh}=-\frac{\hbar^2}{2m_{e}}\left(4.1k^2+\sqrt{1.21k^4+4.1(k_x^2k_y^2+k_x^2k_z^2+k_y^2k_z^2)}\right), \end{equation} \]These bands are quadratic but anisotropic. They are sometimes approximated by isotropic bands described by effective masses,
\[ \begin{equation} E_{v,lh}\approx -\frac{\hbar^2k^2}{2m_{lh}}, \end{equation} \]and
\[ \begin{equation} E_{v,hh}\approx -\frac{\hbar^2k^2}{2m_{hh}}. \end{equation} \]The split-off band is isotropic,
\[ \begin{equation} E_{v,so}=-E_{so}-\frac{\hbar^2k^2}{2m_{so}}. \end{equation} \]For silicon, $m_{lh}= 0.16m_e$, $m_{hh}= 0.49m_e$, $m_{so}= 0.24m_e$, and $E_{so} = 0.035\,\text{eV}$.