Exercise questions 2: Molecules

The starting point for the quantum description of any molecule or crystal is the many-electron Hamiltonian,

\[ \begin{equation} H_{\text{me}}= -\sum\limits_i \frac{\hbar^2}{2m_e}\nabla^2_i -\sum\limits_a \frac{\hbar^2}{2m_a}\nabla^2_a -\sum\limits_{a,i} \frac{Z_ae^2}{4\pi\epsilon_0 |\vec{r}_i-\vec{r}_a|}+\sum\limits_{i< j} \frac{e^2}{4\pi\epsilon_0 |\vec{r}_i-\vec{r}_j|}+\sum\limits_{a< b} \frac{Z_aZ_be^2}{4\pi\epsilon_0 |\vec{r}_a-\vec{r}_b|} . \end{equation} \]

The first sum describes the kinetic energy of the electrons. The electrons are labeled with the subscript $i$. The second sum describes the kinetic energy of all of the atomic nuclei. The atoms are labeled with the subscript $a$. The third sum describes the attractive Coulomb interaction between the positively charged nuclei and the negatively charge electrons. $Z_a$ is the atomic number (the number of protons) of nucleus $a$. The fourth sum describes the repulsive electron-electron interactions. Notice the plus sign before the sum for repulsive interactions. The fifth sum describes the repulsive nuclei-nuclei interactions.

This Hamiltonian neglects some small details like the spin-orbit interaction and the hyperfine interaction. These effects will be ignored in this discussion. If they are relevant, they could be included as perturbations later. Remarkably, this Hamiltonian can tell us the shape of every molecule and the energy released (or absorbed) in a chemical reaction. Any observable quantity of any solid can also be calculated from this Hamiltonian. It turns out, however, that solving the Schrödinger equation associated with this Hamiltonian is usually terribly difficult. Here we will present a standard approach to determine approximate solutions to the Schrödinger equation.

An approximate solution of the many-electron Hamiltonian for a molecule can be found by applying the Born-Oppenheimer approximation and neglecting the electron-electron interactions. The resulting Hamiltonian is called the reduced Hamiltonian. The reduced Hamiltonian is the sum of $N_e$ identical molecular orbital Hamiltonians where $N_e$ is the number of electrons in the molecule.

\begin{equation} H_{\text{red}}= \sum \limits_{i=1}^{N_e} H_{\text{mo}}. \end{equation}

2.1 Explain the Born-Oppenheimer approximation.

2.2 What are the molecular orbital Hamiltonians $H_{\text{mo}}$ for H₂O, O₂, and CH₄?

Molecular orbitals are used in a similar way as hydrogen wave functions are used to construct the many-electron wave functions of atoms. In the simplest approximation, the molecular orbitals are the wave function of a single electron moving in a potential created by all of the positively charged nuclei in a molecule. The molecular orbital Hamiltonian can be written,

\[ \begin{equation} H_{\text{mo}}= - \frac{\hbar^2}{2m_e}\nabla^2 -\sum\limits_{a} \frac{Z_ae^2}{4\pi\epsilon_0 |\vec{r}-\vec{r}_a|}. \end{equation} \]

Here $\vec{r}_a$ are the positions of the nuclei in the molecule and $\vec{r}$ is the position of the single electron. The molecular orbital Hamiltonian is often solved by a method called the Linear Combination of Atomic Orbitals (LCAO). It is assumed that the wave function can be written in terms of atomic orbitals that are centered around the nuclei,

\begin{equation} \psi_{\text{mo}}(\vec{r})= \sum\limits_{a} \sum\limits_{ao} c_{ao,a}\phi^{Z_a}_{ao}\left(\vec{r}-\vec{r}_a\right). \end{equation}

where $ao$ labels the atomic orbitals ($ao=1$: 1s, $ao=2$: 2s, $ao=3$: 2_px, $\cdots$). The number of molecular orbitals that we calculate will be equal to the number of unknown coefficients. We call this number $N$. We have to decide how many atomic orbitals should be included for each atom. A reasonable choice is to take all of the occupied atomic orbitals of the isolated atoms. For instance, for water one might use the 1s, 2s, and 2p orbitals of oxygen and the 1s orbitals of the two hydrogen atoms. In that case, there would be $N=7$ terms in the wave function for the molecular orbital. There is no strict rule as to which atomic orbitals to include. Including more atomic orbitals leads to a higher accuracy but makes the numerical calculation more difficult.

At this point it is convenient to relabel the atomic orbitals used in the wave function with integers $p=1\cdots N$. For water we might choose $\phi_1 = \phi^{Z=1}_{\text{1s}}\left(\vec{r}-\vec{r}_{\text{H1}}\right)$, $\phi_2 = \phi^{Z=1}_{\text{1s}}\left(\vec{r}-\vec{r}_{\text{H2}}\right)$, $\phi_3 = \phi^{Z=8}_{\text{1s}}\left(\vec{r}-\vec{r}_{\text{O}}\right)$, $\phi_4 = \phi^{Z=8}_{\text{2s}}\left(\vec{r}-\vec{r}_{\text{O}}\right)$, etc. The trial wave function can then be written more compactly as,

\begin{equation} \psi_{\text{mo}} = \sum\limits_{p=1}^N c_p\phi_p. \end{equation}

The time independent Schrödinger equation is,

\[ \begin{equation} H_{\text{mo}}\psi_{\text{mo}}=E\psi_{\text{mo}} . \end{equation} \]

Multiply the Schrödinger equation from the left by each of the atomic orbitals and integrate over all space. This results in a set of $N$ algebraic equations called the Roothaan equations.

\[ \begin{equation} \begin{matrix} \large \langle \phi_1 | H_{\text{mo}} |\psi_{\text{mo}}\rangle =E\langle\phi_1|\psi_{\text{mo}} \rangle \\ \large \langle \phi_2 | H_{\text{mo}} |\psi_{\text{mo}}\rangle =E\langle\phi_2|\psi_{\text{mo}} \rangle\\ \large \vdots \\ \large \langle \phi_N | H_{\text{mo}} |\psi_{\text{mo}}\rangle =E\langle\phi_N|\psi_{\text{mo}} \rangle \end{matrix} \end{equation} \]

By substituting in the form for $\psi_{\text{mo}}$ from above, the Roothaan equations can be written in matrix form,

\[ \begin{equation} \left[ \begin{matrix} H_{11} & H_{12} & \cdots & H_{1N} \\ H_{21} & H_{22} & \cdots & H_{2N} \\ \vdots & \vdots & \ddots & \vdots \\ H_{N1} & H_{N2} & \cdots & H_{NN} \end{matrix} \right] \left[ \begin{matrix} c_1 \\ c_2 \\ \vdots \\ c_N \end{matrix} \right] = E\left[ \begin{matrix} S_{11} & S_{12} & \cdots & S_{1N} \\ S_{21} & S_{22} & \cdots & S_{2N} \\ \vdots & \vdots & \ddots & \vdots \\ S_{N1} & S_{N2} & \cdots & S_{NN} \end{matrix} \right] \left[ \begin{matrix} c_1 \\ c_2 \\ \vdots \\ c_N \end{matrix} \right]. \end{equation} \]

Here the elements of the Hamiltonian matrix and the overlap matrix are,

\[ \begin{equation} H_{pq}= \langle\phi_{p}|H_{\text{mo}}|\phi_{q}\rangle \hspace{1cm}\text{and}\hspace{1cm} S_{pq}= \langle\phi_{p}|\phi_{q}\rangle . \end{equation} \]

The Roothaan equations can be solved numerically to find $N$ solutions for the energy $E$ along with the corresponding coefficients that describe the $N$ wave functions which are the molecular orbitals.

The Hückel model is an approximation that is often made to simplify the Roothaan equations. The overlap matrix is nearly the identity matrix. For normalized atomic orbitals, $S_{pp}= 1$ so all of the diagonal elements equal $1$. If two wave functions $\phi_p$ and $\phi_q$ are not the same but are centered on the same nucleus then $S_{pq}= 0$ because the hydrogen atomic orbitals are orthogonal to each other. If two wave functions $\phi_p$ and $\phi_q$ are centered on different nuclei that are far apart in the molecule, then $S_{pq}\approx 0$. This only leaves off-diagonal elements of the matrix that correspond to two wave functions $\phi_p$ and $\phi_q$ that are centered on nearby atoms. Although these elements may not really be zero, they will be small compared to $1$ and we make the approximation,

\[ \begin{equation} S_{pp}= 1 \hspace{1cm} \text{and} \hspace{1cm} S_{pq}= 0 \hspace{1cm} \text{for }p\ne q. \end{equation} \]

The equations that need to be solved reduce to an eigenvalue problem,

2.3 What are the Roothaan equations? What is the Hückel model?

2.4 What are molecular orbitals? How do you calculate them?

2.5 The molecular ion H₂⁺ consists of one electron and two protons.

(a) Explain the Born-Oppenheimer approximation. What is the Schrödinger equation for the electron when the Born-Oppenheimer approximation is used?

(b) Assuming that the wave function can be expressed as a linear combination of atomic orbitals of the form $\psi=c_1\phi_{\text{1s}}(\vec{r}-\vec{r}_A) +c_2\phi_{\text{1s}}(\vec{r}-\vec{r}_B)$, construct the two molecular orbitals and plot them.

(c) Consider the case that the protons are moved far apart. What are the values of the energies of the two molecular orbitals in this limit?

(d) Draw the potential energy of the electron along the interatomic axis under the assumption that the bondlength is 1.06 Å.

2.6 The energies of the first few molecular orbitals for homonuclear diatomic molecules are ordered $1\sigma_g \lt 1\sigma_u \lt 2\sigma_g \lt 2\sigma_u \lt 3\sigma_g \approx 1\pi_u \lt 1\pi_g \lt 3\sigma_u$. The $\sigma$ orbitals are singly degenerate (they can hold 2 electrons) but the $\pi$ orbitals are doubly degenerate (they can hold 4 electrons). $1\pi_u$ is lower in energy than $3\sigma_g$ up to and including N₂ but $3\sigma_g$ is lower in energy for atoms with more electrons than nitrogen.

Specify the ground state of H₂, N₂, Li₂⁺, Be₂, C₂, and O₂.

2.7 A linear combination of atomic orbitals used to find the molecular orbitals of a He₂ molecule contains four atomic orbitals,

\[ \begin{equation} \psi(\vec{r})= c_1\phi^{Z=2}_{\text{1s}}\left(\vec{r}-\vec{r}_{\text{He1}}\right)+c_2\phi^{Z=2}_{\text{1s}}\left(\vec{r}-\vec{r}_{\text{He2}}\right)+c_3\phi^{Z=2}_{\text{2s}}\left(\vec{r}-\vec{r}_{\text{He1}}\right)+c_4\phi^{Z=2}_{\text{2s}}\left(\vec{r}-\vec{r}_{\text{He2}}\right). \end{equation} \]

What is the integral that needs to be evaluated to determine the Hamiltonian matrix element $H_{12}$ for this molecule? What is the integral that needs to be evaluated to determine the matrix element of the overlap matrix $S_{13}$ in the Roothaan equations? This integral is easy to evaluate. What is $S_{13}$?

2.8 Use a database (such as the one embedded in jmol) to determine the Si-O bond length and the angle formed by the atoms Si-O-C in tetraethyl orthosilicate (TEOS).

2.9 Aromatic molecules are substances which are chemically unreactive. In this exercise, we will compare the prototypical aromat benzene with its linear chain equivalent, 1,3,5-hexatriene (shown in the picture below).

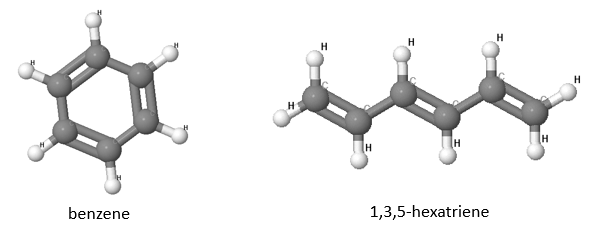
(a) How many $p_z$ electrons are in these two molecules?

(b) Set up the the Roothaan-equations for both molecules assuming that only the $p_z$ orbitals need to be included. Look at the discussion of molecular orbitals of a conjugated rings and the molecular orbitals of conjugate chains. Use $H_{11} = - 12$ eV, $H_{12} = -3.8$ eV, $S_{11} = 1$, and $S_{12} = 0.27$. These are not the values that the simple model gives but are close to the observed values.

(c) Which molecular orbitals will be occupied for benzene and for 1,3,5-hexatriene? Which molecular orbitals are degenerate? (Degenerate molecular orbitals have the same energy).

(d) The total energy of the molecules can be approximated as the sum over all occupied molecular orbitals. Which molecule has the lower energy?

(e) Calculate and compare the energy difference between the highest occupied molecular orbital and the lowest unoccupied molecular orbital for both molecules. This energy difference could be measured spectroscopically.

2.10 If exercise 2.3 is repeated for the case of 4 carbon atoms (ring = cyclobutadiene, chain = butadiene), the chain turns out to have a lower energy than the ring. Show this.

2.11 The cation of cyclopropene is the smallest aromatic molecule. The Roothaan equations can be used to express three molecular orbitals in terms of the three $2p_z$ orbitals. Use $H_{11} = - 12$ eV, $H_{12} = -3.8$ eV, $S_{11} = 1$, and $S_{12} = 0.27$.

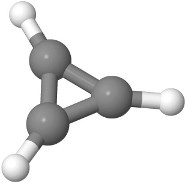
(a) The cation of cyclopropene has one less electron than neutral cyclopropene. How many electrons are in the cation in total? How many electrons are in the molecular $\pi$-system and have to be accounted for in the Roothaan equations?

(b) Calculate the energies of the orbitals. What is the degeneracy of the unoccupied orbitals?

(c) The molecule can absorb a photon to promote one electron from the highest occupied molecular orbital to the lowest unoccupied molecular orbital. What is the wavelength of the photon?

2.12 The molecular orbitals of all homonuclear diatomic molecules (H₂, N₂, O₂, etc.) all have a similar structure. Explain what is the same and what is different between the molecular orbitals of these molecules.

2.13 Consider H₂, and He₂. How many molecular orbitals are occupied for each of these molecules? The molecular orbital energies are calculated as for H_2⁺,

\begin{equation} E_{+}= \frac{H_{11}+ H_{12}}{1+ S_{12}}, \qquad E_{-}= \frac{H_{11}- H_{12}}{1- S_{12}}. \end{equation}

Show that for H₂ the sum energy of the occupied molecular orbitals is less than the energy of the isolated H atoms (=$2H_{11}$) while for He₂ the energy of the molecule is larger than the isolated He atoms.

Multi-electron wave functions consisting of any product of molecular orbitals solve the reduced electronic Hamiltonian. However, not all such solutions are physically relevant because in addition to being a solution to the Schrödinger equation, multielectron wave functions must also be antisymmetric. The common way to construct a properly antisymmetrized multi-electron wave function is to use a Slater determinant. An estimation of the energy of a multi-electron molecular state can be made by calculating the energy,

\[ \begin{equation} E= \frac{ \langle \Psi(\vec{r}_1,\vec{r}_2,\cdots,\vec{r}_{N_e})|H_{\text{elec}}|\Psi(\vec{r}_1,\vec{r}_2,\cdots,\vec{r}_{N_e})\rangle}{\langle \Psi(\vec{r}_1,\vec{r}_2,\cdots,\vec{r}_{N_e})|\Psi(\vec{r}_1,\vec{r}_2,\cdots,\vec{r}_{N_e})\rangle} \end{equation} \]

Here $\Psi(\vec{r}_1,\vec{r}_2,\cdots,\vec{r}_{N_e})$ is an antisymmetrized wave function with $N_e$ electrons and $H_{\text{elec}}$ is the electronic Hamiltonian which includes the electron-electron interactions. The integrals that have to be performed to calculate the energy are defined in $3N_e$ dimensions. When comparing the energies of two molecular states, only include the valence molecular orbitals so that integrals do not become too computationally intensive. In practice, a numerical approach such as density functional theory or the Hartree_Fock method is often used to find the molecular orbitals. We will not discuss these advanced methods in this course.

Being able to calculate the energy of a molecular state is very powerful because molecules will go to a minimum of the energy. The bond potential of a chemical bond can be calculated by changing the distance between the atoms that form that bond, finding the molecular orbitals and then using the molecular orbitals to calculate the energy of the multi-electron state for each distance. Don't forget to include the change in energy of the nuclei-nuclei interaction as the distance between the nuclei changes. This calculation yields the equilibrium bond length and the bond strength. Similarly, bond angles can be calculated by determining which angle gives the lowest energy. The energy released in a chemical reaction can be found by subtracting the energies of the products from the energies of the reactants.

2.14 The bond length and the bond energy of a C-C bond depends on the other atoms in the molecule. How do you calculate the bond potential for a particular C-C bond in a molecule?

2.15 How could the H-N-H bond angle be calculated for NH₃?

2.16 Molecular orbitals for water are calculated using the LCAO method by assuming a molecular orbital that is a linear combination of the two hydrogen $1\text{s}$ orbitals plus the oxygen $1\text{s}$, $2\text{s}$, $2\text{p}_x$, $2\text{p}_y$, and $2\text{p}_z$ orbitals. How many molecular orbitals will be calculated? How many of the molecular orbitals are filled in the ground state of the molecule? The energy is of the many-electron ground state calculated including all of the electrons of the molecule in the Slater determinant, how many dimensions is the integral $\langle \Psi(\vec{r}_1,\vec{r}_2,\cdots,\vec{r}_{N_e})|H_{\text{elec}}|\Psi(\vec{r}_1,\vec{r}_2,\cdots,\vec{r}_{N_e})\rangle$ defined in?

2.17 How can you calculate the energy released when one methane molecule burns in oxygen to form water and carbon dioxide?

2.18 How do you calculate the bond potential for a

Polar bond?
Covalent bond?
Van der Waals bond?
Hydrogen bond?
double bond?
triple bond?

Although the bond potentials of any bond is calculated the same way, they are often fit to different bond potentials. For covalent bonds, the Morse potential is often used,

\begin{equation} U(r)= U_0\left(e^{-2a(r-r_0)}-2e^{-a(r-r_0)}\right). \end{equation}

For van der Waals bonds, a Lennard-Jones potential is often used,

\begin{equation} U(r)= U_0\left(\left(\frac{r_0}{r}\right)^{12}-2\left(\frac{r_0}{r}\right)^{6}\right). \end{equation}

Here $r$ is the distance between the atoms and $r_0$ is the minimum of the potential. For diatomic molecules, the bond potentials can be used to find the vibrational and rotational spectra of a molecule. Diatomic molecules only have one stretching mode where the two atoms in a molecule vibrate with respect to each other. In the simplest approximation, we imagine that the atoms are attached to each other by a linear spring. The spring constant can be determined from the bond potential. Near the minimum of the bond potential at $r_0$, the potential can be approximated by a parabola. This is the same potential as for a harmonic oscillator where the effective spring constant is $k_{\text{eff}}=\frac{d^2U}{dr^2}|_{r=r_0}$ and the reduced mass is $m_r=(1/m_a+1/m_b)^{-1}$. Here $m_a$ and $m_b$ are the masses of the two atoms. The angular frequency of this vibration is $\omega=\sqrt{k_{\text{eff}}/m_r}$. The vibrational modes of the molecule have the same energy level spectrum as a harmonic oscillator,

\[ \begin{equation} E_{\nu}=\hbar\omega(\nu+1/2) \hspace{1.5cm} \nu=0,1,2,\cdots. \end{equation} \]

The rotational levels of a diatomic molecule can be estimated by assuming that the atoms remain at their equilibrium spacing $r_0$ during rotation. In this can, the quantized energy levels of a rigid rotator can be used,

\[ \begin{equation} E_{\mathcal{l}}= \frac{\hbar^2}{2I}\mathcal{l}(\mathcal{l}+1), \end{equation} \]

where $I$ is the moment of inertia and $\mathcal{l}$ is orbital quantum number, $\mathcal{l}=0,1,2,\cdots$. For a diatomic molecule with an equilibrium spacing of the atoms of $r_0$ and atomic masses $m_a$ and $m_b$, the moment of inertia is $I=\frac{m_am_b}{m_a+m_b}r_0^2$.

2.19 The $\nu = 0$ to $\nu = 1$ vibrational transition of an HI molecule occurs at a frequency of $6.69\times 10^{13}$ Hz. The same transition for the NO molecule occurs at a frequency of $5.63 \times 10^{13}$ Hz. The atomic masses (in atomic units) are: I = 126.9, H = 1.01, N = 14.01, O = 16. Calculate:

(a) The effective force constants.

(b) The classical amplitude of vibration for each molecule for $\nu = 10$.

2.20 The potential energy of a diatomic molecule is $U(R)=-\frac{\alpha}{ R^4}+\frac{\beta}{ R^{12}}$, with $\alpha$ and $\beta$ being characteristic constants for the molecule.

(a) Find the interaction force between the two atoms as a function of distance $R$.

(b) Find the equilibrium spacing $R_0$ between the two atoms.

2.21 The bond potential of a diatomic molecule has a Lennard-Jones form, $U(R)=-\frac{A}{ R^6}+\frac{B}{ R^{12}}$. The bondlength of this molecule is 3 Å and the dissociations energy is 1.8 eV.

(a) Calculate $A$ and $B$.

(b) A force is applied that separates the molecule. As this force is slowly increased the atoms move further apart until a critical distance where the molecule suddenly dissociates. What is the critical distance and what is the force at this point?

2.22 What are the rotational energy levels of an CO molecule? The bond length is 112.8 pm.

2.23 Calculate the moment of inertia of CHCl₃ for rotation around the C-H bond. Calculate the three principle moments of inertia of a water molecule. The principle moments of inertia are,

$$I_{xx}= \sum_i m_i(y_i^2+z_i^2),\qquad I_{yy}= \sum_i m_i(x_i^2+z_i^2),\qquad I_{zz}= \sum_i m_i(x_i^2+y_i^2),$$

where $i$ sums over the atoms, $m_i$ are the masses of the atoms, and the distances are measured from the center of mass. Use an online database such as JSmol molecule viewer to determine the bond lengths and bond angles. The moment of inertia depends on the isotopes of the atoms. In this case, it does not make sense to use an average atomic mass. Use the isotopes ¹H ¹⁶O, ¹²C, and ³⁵Cl.

2.24 The rotational spectrum of ⁷⁹Br¹⁹F has a uniform line spacing of 0.71433 cm^-1. In the rigid rotator model, the rotational energies are given by,

$$E_{J}= \frac{\hbar^2}{2I}J(J+1)=BJ(J+1)\qquad J= 0,1,2,\cdots,$$

where $B$ is the rotation constant and $I$ is the moment of inertia of the molecule. For a diatomic molecule,

$$I=\frac{m_am_b}{m_a+m_b}r_0^2,$$

where $r_0$ is the bond length. Rotational transitions are allowed for $\Delta J = \pm 1$.

Calculate the rotation constant $B$, the moment of inertia, and the bond length of the molecule. Determine the wave number of the transition $J = 9 \rightarrow 10$. For the state $J = 10$, calculate the classical number of rotations per second.

2.25 A Morse potential is often used to approximate the bond potential of a covalent bond.

$$U(r)= U_0\left(e^{-2a(r-r_0)}-2e^{-a(r-r_0)}\right)$$

For a Morse potential with $U_0=1.76\,\text{eV}$, $r_0=1.1$ Å, and $a=9\times 10^{10}\,\text{1/m}$, determine the spacing of the vibrational levels by approximating the minimum of the potential using a parabola. For the mass, use the reduced mass of N₂, $m=1.16\times 10^{-26}$ kg.

For molecules with more than two atoms, a multidimensional potential energy can be constructed by calculating the energy for the atoms of the molecule being in different positions. This potential energy has a minimum when all of the atoms are in their equilibrium positions. For small displacements from the minimum it is possible to model this as a collections of masses attached by linear springs. A molecule with $n$ atoms has $3n$ degrees of freedom. Let $u_1$ be the displacement of the first atom from its equilibrium position in the $x$-direction, $u_2$ be the displacement of the first atom from its equilibrium position in the $y$-direction, $u_3$ be the displacement of the first atom from its equilibrium position in the $z$-direction, $u_4$ be the displacement of the second atom from its equilibrium position in the $x$-direction, etc. Newton's law in this case takes the form of $3n$ second order differential equations,

\[ \begin{eqnarray} m_1\frac{d^2u_1}{dt^2} = k_{12}(u_2-u_1)+ k_{13}(u_3-u_1)+\cdots+k_{1,3n}(u_{3n}-u_1)\\ m_1\frac{d^2u_2}{dt^2} = k_{12}(u_1-u_2)+ k_{23}(u_3-u_2)+\cdots+k_{2,3n}(u_{3n}-u_2)\\ m_1\frac{d^2u_3}{dt^2} = k_{13}(u_1-u_3)+ k_{23}(u_2-u_3)+\cdots+k_{3,3n}(u_{3n}-u_3)\\ % requires corrected spring constants %m_2\frac{d^2u_4}{dt^2} = k_{12}(u_1-u_4)+ k_{23}(u_2-u_4)+\cdots+k_{4,3n}(u_{3n}-u_4)\\ %m_2\frac{d^2u_5}{dt^2} = k_{12}(u_1-u_5)+ k_{23}(u_2-u_5)+\cdots+k_{5,3n}(u_{3n}-u_5)\\ %m_2\frac{d^2u_6}{dt^2} = k_{12}(u_1-u_6)+ k_{23}(u_2-u_6)+\cdots+k_{6,3n}(u_{3n}-u_6)\\ % m_2\frac{d^2u_4}{dt^2} = k_{14}(u_1-u_4)+ k_{24}(u_2-u_4)+\cdots+k_{4,3n}(u_{3n}-u_4)\\ m_2\frac{d^2u_5}{dt^2} = k_{15}(u_1-u_5)+ k_{25}(u_2-u_5)+\cdots+k_{5,3n}(u_{3n}-u_5)\\ m_2\frac{d^2u_6}{dt^2} = k_{16}(u_1-u_6)+ k_{26}(u_2-u_6)+\cdots+k_{6,3n}(u_{3n}-u_6)\\ \end{eqnarray} \] \[ \begin{equation} \vdots \end{equation} \] \[ \begin{eqnarray} m_n\frac{d^2u_{3n-2}}{dt^2} = k_{1,3n-2}(u_1-u_{3n-2})+ k_{2,3n-2}(u_2-u_{3n-2})+\cdots+k_{3n-2,3n}(u_{3n}-u_{3n-2})\\ m_n\frac{d^2u_{3n-1}}{dt^2} = k_{1,3n-1}(u_1-u_{3n-1})+ k_{2,3n-1}(u_2-u_{3n-1})+\cdots+k_{3n-1,3n}(u_{3n}-u_{3n-1})\\ m_n\frac{d^2u_{3n}}{dt^2} = k_{1,3n}(u_1-u_{3n})+ k_{2,3n}(u_2-u_{3n})+\cdots+k_{3n-1,3n}(u_{3n-1}-u_{3n})\\ \end{eqnarray} \]

For a normal mode solution, all of the atoms move with the same frequency $u_p=A_pe^{i\omega t}$, where $A_p$ is the amplitude of displacement $p=1,2,\cdots,3n$. Substituting this into the equations above results in an eigenvalue problem.

\[ \begin{equation} \left[ \begin{matrix} \sum\limits_{p\neq 1} \frac{k_{1p}}{m_1} & -\frac{k_{12}}{m_1} & -\frac{k_{13}}{m_1} & \cdots & -\frac{k_{1,3n}}{m_1} \\ -\frac{k_{21}}{m_1} &\sum\limits_{p\neq 2} \frac{k_{2p}}{m_1}& -\frac{k_{23}}{m_1} & \cdots & -\frac{k_{2,3n}}{m_1} \\ -\frac{k_{31}}{m_1} & -\frac{k_{32}}{m_1} & \sum\limits_{p\neq 3} \frac{k_{3p}}{m_1} & \cdots & -\frac{k_{3,3n}}{m_1} \\ & \vdots & & \\ -\frac{k_{1,3n-2}}{m_n} & \cdots & \sum\limits_{p\neq 3n-2} \frac{k_{p,3n-2}}{m_n} & -\frac{k_{3n-1,3n-2}}{m_n} & -\frac{k_{3n,3n-2}}{m_n} \\ -\frac{k_{1,3n-1}}{m_n} & \cdots & -\frac{k_{3n-2,3n-1}}{m_n} & \sum\limits_{p\neq 3n-1} \frac{k_{p,3n-1}}{m_n} & -\frac{k_{3n,3n-1}}{m_n} \\ -\frac{k_{1,3n}}{m_n} & \cdots & -\frac{k_{3n-2,3n}}{m_n} & -\frac{k_{3n-1,3n}}{m_n} & \sum\limits_{p\neq 3n} \frac{k_{p,3n}}{m_n} \\ \end{matrix} \right] \left[ \begin{matrix} A_{1} \\ A_{2} \\ A_{3} \\ \vdots \\ A_{3n-1} \\ A_{3n-2} \\ A_{3n} \end{matrix} \right]=\omega^2\left[ \begin{matrix} A_{1} \\ A_{2} \\ A_{3} \\ \vdots \\ A_{3n-1} \\ A_{3n-2} \\ A_{3n} \end{matrix} \right] \end{equation} \]

Here $k_{pq}=k_{qp}$ is the effective spring constant between describing how the energy increases as $u_p-u_q$ increases. Of the $3n$ degrees of freedom, three correspond to the translation of the center of mass of the molecule. The potential energy of the mass spring system does not change if the whole molecule is translated. The mathematical consequence of this is that there are three eigenvectors that describe the center-of-mass motion which have an eigenvalue zero. The potential energy of the molecule also does not depend on the orientation of the molecule. This means that the eigenvectors that correspond to the rotational degrees of freedom also have eigenvalues of zero. There are two rotational degrees of freedom for linear molecules where the atoms are all in a line and three rotational degrees of freedom for nonlinear molecules. The rest of the eigenvectors correspond to vibrational normal modes. There are $N_{\text{vib}}=3n-5$ vibrational modes for linear molecules and $N_{\text{vib}}=3n-6$ vibrational modes for nonlinear molecules.

The state of a molecule is described by its electronic state (how the electrons occupy the molecular orbitals) plus its vibrational state plus its rotational state. A molecule can change states by interacting with electro-magnetic waves. Molecules can absorb a photon of energy $\hbar \omega$ if that photon has the energy to move an electron from an occupied state to an unoccupied state, $\hbar \omega = \Delta E_{\text{elec}}+\Delta E_{\text{vib}}+\Delta E_{\text{rot}}$. If a molecule is in a state other than the ground state, it can also emit a photon such that $\hbar \omega = \Delta E_{\text{elec}}+\Delta E_{\text{vib}}+\Delta E_{\text{rot}}$. Transitions that involve a change in the electronic state typically result in the emission of a visible photon. Transitions where the electronic configuration of the electrons stays the same but the vibrational state changes typically result in the emission of an infrared photon. Transitions where the electronic configuration of the electrons stays the same and the vibrational state stays the same but the rotational state changes typically result in the emission of a microwave photon. Although the transition from any state to any other state is possible, some transitions occur at a very low rate. The absorption spectrum or emission spectrum of a molecule tends to be dominated by the transitions that occur at a high rate. The adsorption and emission spectra of a molecule are unique for that molecule and can be used as a means of measuring the presence of a specific molecule.

2.26 (a) How many vibrational modes do CO₂ and H₂O have?

(b) An N₂ molecule is in its electronic ground state and its vibronic ground state. Which rotational states would be occupied at room temperature? (The app on Rotational and vibrational energy levels of diatomic molecules includes N₂. Room temperature corresponds to an energy of about 0.025 eV. )

2.27 Calculate the force constant of the C-O bond from the oscillation frequency of the CO molecule (6.42 × 10¹³ Hz). Further demonstrate that at room temperature most of the molecules of a CO gas sample are in excited states.

2.28 Which normal vibrational modes are excitable for the linear carbon dioxide molecule CO₂ and for the bent water molecule H₂O? Illustrate this schematically by arrows indicating the movement of the atoms.

2.29 How do the molecular orbitals tell you if the hybridization of a carbon atom is sp, sp², or sp³?

2.30 How do the molecular orbitals tell you if a bond is a single bond or a double bond?

2.31 (old exam question) The many particle Hamiltonian for any molecule or solid is,

\begin{equation} \label{eq:htotal} H_{\text{mp}}= -\sum\limits_i \frac{\hbar^2}{2m_e}\nabla^2_i -\sum\limits_a \frac{\hbar^2}{2m_a}\nabla^2_a -\sum\limits_{a,i} \frac{Z_ae^2}{4\pi\epsilon_0 |\vec{r}_i-\vec{r}_a|}+\sum\limits_{i< j} \frac{e^2}{4\pi\epsilon_0 |\vec{r}_i-\vec{r}_j|}+\sum\limits_{a< b} \frac{Z_aZ_be^2}{4\pi\epsilon_0 |\vec{r}_a-\vec{r}_b|} . \end{equation}

\begin{equation} H_{\text{red}}= \sum \limits_{i=1}^{N_e} H_{\text{mo}}. \end{equation}

(a) Explain what the Born-Oppenheimer approximation is and why it is possible to use this approximation.

Acetylene C₂H₂ consists of two carbon atoms ($Z=6$) at positions $\vec{r}_{C1}$, $\vec{r}_{C2}$ and two hydrogen atoms ($Z=1$) at positions $\vec{r}_{H1}$, $\vec{r}_{H2}$.

(b) What is the molecular orbital Hamiltonian for acetylene?

$H_{\text{mo}}=$

(c) In the linear combination of atomic orbitals, what trial wave function would you use to solve the molecular orbital Hamiltonian? Write the atomic orbitals in a format like $\phi_{1s}^\text{H}(\vec{r}-\vec{r}_{H1})$.

$\psi_{\text{mo}}=$

(d) How many of the molecular orbitals that will be calculated with your trial wave function from part (c) will be occupied in the ground state of acetylene?

(e) How many vibrational and how many rotational modes does an acetylene molecule have?