PHY.K02UF Molecular and Solid State Physics
|
| ||||
PHY.K02UF Molecular and Solid State Physics | ||||
Every periodic function has a Bravais lattice and a corresponding reciprocal lattice. The relations between the primitive lattice vectors in real space and in reciprocal space are,
\[ \begin{eqnarray} \vec{b}_1=2\pi \frac{\vec{a}_2\times\vec{a}_3}{\vec{a}_1\cdot\left(\vec{a}_2\times\vec{a}_3\right)}&\hspace{2cm}&\vec{a}_1=2\pi \frac{\vec{b}_2\times\vec{b}_3}{\vec{b}_1\cdot\left(\vec{b}_2\times\vec{b}_3\right)} \\ \vec{b}_2=2\pi \frac{\vec{a}_3\times\vec{a}_1}{\vec{a}_1\cdot\left(\vec{a}_2\times\vec{a}_3\right)}&\hspace{2cm}&\vec{a}_1=2\pi \frac{\vec{b}_3\times\vec{b}_1}{\vec{b}_1\cdot\left(\vec{b}_2\times\vec{b}_3\right)} \\ \vec{b}_3=2\pi \frac{\vec{a}_1\times\vec{a}_2}{\vec{a}_1\cdot\left(\vec{a}_2\times\vec{a}_3\right)}&\hspace{2cm}&\vec{a}_3=2\pi \frac{\vec{b}_1\times\vec{b}_2}{\vec{b}_1\cdot\left(\vec{b}_2\times\vec{b}_3\right)} \end{eqnarray} \]The inner product of the primitive lattice vectors in real space and the primitive latice vectors in reciprocal space satisfy,
$$\vec{a}_i\cdot\vec{b}_j=2\pi\delta_{ij},$$where $\delta_{ij}$ is the Kronecker delta.
A reciprocal lattice vector can be written in term of the primitive lattice vectors in reciprocal space,
\[ \begin{equation} \vec{G}=\nu_1\vec{b}_1+\nu_2\vec{b}_2+\nu_3\vec{b}_3, \end{equation} \]where $\nu_1, \nu_2, \nu_3$ are integers. The reciprocal lattice vectors can be used to write a periodic function $f(\vec{r})$ as a Fourier series,
\[ \begin{equation} f(\vec{r})=\sum\limits_{\vec{G}}f_{\vec{G}}e^{i\vec{G}\cdot\vec{r}}. \end{equation} \]Here $f_{\vec{G}}$ are complex coefficients called the structure factors.
For the exam you should be able to determine the reciprocal lattice vectors of any Bravais lattice and know that the reciprocal lattice of an orthorhombic lattice with lattice constants $(a,b,c)$ is also an orthorhombic lattice $(2\pi /a,2\pi /b,2\pi /c)$ and the reciprocal lattice of fcc is bcc and the reciprocal lattice of bcc is fcc.
4.1 Determine the reciprocal lattice of a monoclinic crystal $a = 5$ Å, $b = 8$ Å, $c = 25$ Å, and $\alpha = 98$°. Make a sketch to illustrate the unit cell in the real space and in reciprocal space. Give the length of the unit cell vectors in reciprocal space.
4.2 The function $f(x,y)$ has a periodicity of $a$ in the $x$-direction and $b$ in the $y$-direction,
\[ \begin{equation} f(x,y)=3\sin \left(\frac{2\pi x}{a}\right)\cos \left(\frac{2\pi y}{b}-1\right). \end{equation} \]This function can be expressed as a sum of complex exponentials,
\[ \begin{equation} f(x,y)=\sum\limits_{\vec{G}}f_{\vec{G}}e^{i(G_xx+G_yy)}. \end{equation} \]Calculate Fourier coefficients, $f_{\vec{G}}$.
4.3 Draw the Fourier transform of the function,
\[ \begin{equation} f(x,y)=3\cos (5x) +2\sin (3y). \end{equation} \]You need to draw the amplitudes $f_{\vec{G}}$ at the positions of the reciprocal lattice vectors in reciprocal space. The amplitudes may be complex.
Reciprocal space can be divided into Brillouin zones. The first Brillouin zone is the set of points closer to the origin in reciprocal space than to any other reciprocal lattice vector. It is analogous to the Wigner-Seitz cell in real space. All points outside the first Brillouin zone can be reached by a vector in the first Brillouin zone plus a reciprocal lattice vector. You should be able to construct the first Brillouin zone of any reciprocal lattice.
4.4 (a) Determine the reciprocal lattice of a tetragonal crystal a = b = 5 Å, c = 8 Å.
(b) Make a sketch to illustrate the unit cell in the real space and the first Brillouin zone in reciprocal space. Specify the lengths of the sides of the Brillouin zone. Label the directions in real space and reciprocal space.
4.5 Consider a rhombohedral lattice. All lattice contants have the same length $a=b=c$ and the angles between the primitive lattice vectors are all the same $\alpha = \beta = \gamma$.
Show that the primitive lattice vectors in real space can be chosen to have the form,
\[ \begin{equation} \vec{a}_1 = d_1\hat{x}+d_1\hat{y}+d_2\hat{z}, \\ \vec{a}_2 = d_1\hat{x}+d_2\hat{y}+d_1\hat{z}, \\ \vec{a}_3 = d_2\hat{x}+d_1\hat{y}+d_1\hat{z}. \end{equation} \]Here $d_1$ and $d_2$ are constants. Find the primitive reciprocal lattice vectors and show that the reciprocal lattice is again of rhombohedral type.
4.6 X-rays with an energy of 8 keV are used to analyze a simple orthorhombic lattice ($a=$ 0.6 nm, $b=$ 0.8 nm, $c=$ 0.4 nm). The x-rays propagate in the (001) plane and also the detector scans in the (001) plane. Draw Ewald's sphere in the (001) plane. Label the axes with the [100] and [010] directions.
Draw the reciprocal lattice together with the wave vector of the primary beam $\vec{k}$ as well as the wave vector of the scattered beam $\vec{k}'$ for the reflection 320.
Diffraction occurs when waves strike a periodic structure and the wavelength of the waves is shorter than the periodicity of the structure. Under these conditions, some of the waves will continue in the direction $\vec{k}$ of the primary beam and some will be scattered elastically to directions $\vec{k}'$ where the scattering vector is a reciprocal lattice vector,
\[ \begin{equation} \Delta \vec{k} = \vec{k}' -\vec{k} = \vec{G}. \end{equation} \]This is called the diffraction condition and it is often used to determine crystal structures. In the experiment, a crystal is put in the primary beam of an x-ray diffractometer. For elastic scattering $|\vec{k}|=|\vec{k}'|=2\pi /\lambda$. By detecting the angles at which diffraction peaks are observed, it is possible to calculate the reciprocal lattice vectors from the diffraction condition. If many reciprocal lattice vectors are determined, it is possible to deduce the primitive lattice vectors in reciprocal space,
\[ \begin{equation} \vec{G}=\nu_1\vec{b}_1+\nu_2\vec{b}_2+\nu_3\vec{b}_3\hspace{1.5 cm}\nu_1,\nu_2,\nu_3 = \cdots ,-2,-1,0,1,2,\cdots \end{equation} \]From the primitive lattice vectors in reciprocal space, it is possible to calculate the primitive lattice vectors in real space (the formulas are given at the top of this page). The primitive lattice vectors in real space determine the Bravais lattice and the volume of the unit cell in real space. The atoms in the basis can be determined by comparing the intensities of the diffraction peaks to the structure factors that appear in the Fourier series for the electron density,
\[ \begin{equation} n\left(\vec{r}\right)= \sum\limits_{\vec{T}} \sum\limits_j n_j\left(\vec{r}-\vec{r}_j+\vec{T}\right)=\sum\limits_{\vec{G}}n_{\vec{G}}e^{i\vec{G}\cdot\vec{r}}. \end{equation} \]Here $\vec{T}$ are the translation vectors of the Bravais lattice, $n_j\left(\vec{r}\right)$ is the electron density of atom $j$ and $n_{\vec{G}}$ are the structure factors. The intensity of the diffraction peak $\vec{G}$ is proportional to $|n_{\vec{G}}|^2$. Since most electrons are core electrons, the electron density in a crystal is sharply peaked around the nuclei. A simple approximation for the electron density of a unit cell of a crystal is,
\begin{equation} n(\vec{r})=\sum \limits_j Z_j\delta(\vec{r}-\vec{r}_j). \end{equation}Where $Z_j$ is the atomic number of atom $j$ and $\vec{r}_j$ is the position of atom $j$. In this case, the structure factors are,
\begin{equation} n_{\vec{G}}=\sum \limits_j Z_j\exp (-i\vec{G}\cdot\vec{r}_j), \end{equation}The electron density of an atom can be described more accurately using the atomic form factors listed in the International Tables for Crystallography. The structure factor is calculated from the atomic form factors $f(G)$ as,
\begin{equation} n_{\vec{G}} = \sum\limits_j f_j\left(G\right)e^{-i\vec{G}\cdot\vec{r}_j} = \sum\limits_j f_j\left(G\right)\left(\cos\left(\vec{G}\cdot\vec{r}_j\right)-i\sin\left(\vec{G}\cdot\vec{r}_j\right)\right). \end{equation}To determine how the atoms are arranged in the basis, typically you have to guess the arrangement of the atoms and calculate the resulting structure factors and them compare them to the intensities of the diffraction peaks.
4.7 A simple approximation for the electron density of an atom is the atomic number times a delta function $Z\delta (\vec{r})$. The atomic number $Z$ is the number of electrons that an atom has. In this approximation, the electron density of a crystal is,
$n(\vec{r}) = \sum \limits_{i,l,m,n}Z_i\delta(\vec{r}_i+l\vec{a}_1+m\vec{a}_2+n\vec{a}_3)$,
where $i$ sums over the atoms in the unit cell and the translation vector $\vec{T}_{lmn}=l\vec{a}_1+m\vec{a}_2+n\vec{a}_3$ repeats the unit cell everywhere in the crystal.
(a) Write down the general expression for a 3-D periodic function in terms of a Fourier series.
(b) CsCl has a simple cubic Bravais lattice. $Z_{Cs} = 55$, $Z_{Cl} = 17$. What are the structure factors $G_{000}$ and $G_{100}$?
4.8 The figure below shows a crystallographic unit cell of the double hexagonal close-packed (dhcp) structure of the element americium. The Bravais lattice is hexagonal with $\vec{a}_1 = a\hat{x}, \vec{a}_2 =\frac{a}{2}\hat{x} +\frac{\sqrt{3}a}{2}\hat{y}, ~\text{and}~ \vec{a}_3 = c\hat{z}$. The basis is (0 0 0), (2/3 2/3 1/4), (0 0 1/2) and (1/3 1/3 3/4).
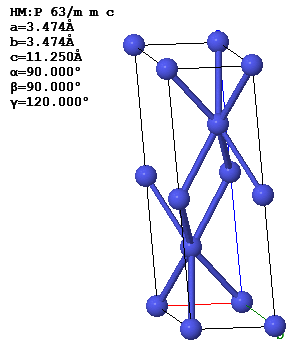
(a) Find the reciprocal lattice vectors $\vec{G}$. Describe in words and sketch the reciprocal lattice.
(b) Sketch the first Brillouin zone. Give values for the important dimensions.
(c) Find the structure factors associated with the points 100, 001, and 120 of reciprocal lattice. Use the atomic form factor app to determine the atomic form factors. Check you results using the structure factor app.
4.9 By performing x-ray diffraction on crystallized proteins, it is possible to determine the type of crystal that is formed and the shape of the proteins. The crystal structure is not important for the biological function of the protein but the shape is very important. How is the shape of the protein determined from x-ray diffraction?
4.10 For the hydrogen atom in its ground state, the electron density is $n(r) = (\pi a_0^3)^{-1}\exp(-2r/a_0)$, where $a_0$ is the Bohr radius. Integrating this expression over all space yields 1 indicating that there is one electron.
\begin{equation} \int \limits_0^{\infty} 4\pi r^2 n(r)dr=1 \end{equation}The atomic form factor is the three-dimensional Fourier transform of the electron density. Show that the atomic form factor is $f_G = 16/(4 + G^2a_0^2)^2$.
4.11 A simple cubic crystal has one atom per unit cell. The electron density in a unit cell can be described by a Gaussian $n(r) = A \exp\left(-a^2r^2\right)$ Å-3. Here $a = 5\times 10^{10}$ and $r$ is measured in meters. The lattice constant is 0.2 nm. What is the ratio of the structure factors $S(111)/S(000)$?
The integral of $n(r)$ over all space is the number of electrons in this atom.
$$Z = A\int\limits_0^{\infty} 4\pi r^2 \exp(-a^2r^2)dr = \frac{\pi\sqrt{\pi}A}{a^3}.$$The atomic form factor $f(q)$ is the Fourier transform of $n(r)$. You can find the Fourier transform of a Gaussian function in the table at the bottom of the page on Fourier transforms,
$$ f(q) = \frac{\pi\sqrt{\pi}A}{a^3} \exp\left(-\frac{q^2}{4a^2}\right).$$4.12 Chromium forms a bcc lattice with a lattice constant of $a=2.91$ Å. There is one atom in the basis $\vec{B}_1 = (0,0,0)$. The primitive lattice vectors are,
$$\vec{a}_1=\frac{a}{2}(\hat{x}+\hat{y}-\hat{z}),\quad \vec{a}_2=\frac{a}{2}(-\hat{x}+\hat{y}+\hat{z}),\quad\vec{a}_3=\frac{a}{2}(\hat{x}-\hat{y}+\hat{z}).$$It is also possible to describe this crystal using the cubic conventional lattice vectors,
$$\vec{a}_1=a\,\hat{x},\quad \vec{a}_2=a\,\hat{y},\quad \vec{a}_3=a\,\hat{z},$$and two atoms in the basis $\vec{B}_1 = (0,0,0),\,\vec{B}_2 = (0.5,0.5,0.5)$. The labeling of the diffraction peaks with Laue indices $hkl$ are different for the two descriptions.
(a) Calculate the interplanar distance $d_{100}$, the structure factor $S_{100}$, and the intensity $I_{100}=S_{100}^2$ of the $100$ reflection using the conventional unit cell.
(b) Calculate the the interplanar distance $d_{110}$, the structure factor $S_{110}$, and the intensity $I_{110}$ of the $110$ reflection using the conventional unit cell.
(c) Calculate the the interplanar distance $d_{100}$, the structure factor $S_{100}$, and the intensity $I_{100}$ of the $100$ reflection using the primitive unit cell.
(d) Compare the Laue indices, interplanar distances, and intensities of the two descriptions.
The atomic form factor for Cr is plotted below.
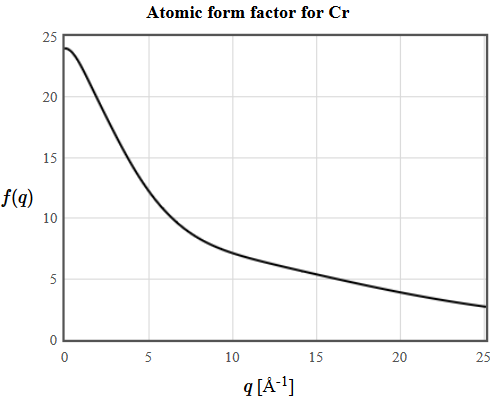
4.13 Determine the lattice parameter of Ni (fcc): The Bragg angle of the (220) reflection is 38.2° and the wavelength of the X-rays is 1.54Å. The netplanes are indexed using the unit vectors of the conventional unit cell.
4.14 When electrons, X-rays, neutrons, or helium are diffracted by a crystal, the same diffraction peaks are observed in each case. However, the intensities of the peaks depend on the type of beam that is diffracted. Why do all of these beams produce the same diffraction peaks and why are the intensities different for the different beams?
4.15 X-ray diffraction is performed on an orthorhomic crystal ($a=$2 nm, $b=3$ nm, $c=1$ nm). The primary x-ray beam propagates within the (001) plane and also the detector scans the (001) plane. The problem is solvable in two dimensions, i.e., Ewald's sphere becomes a circle.
Which reflections are visible in the diffraction pattern when the primary x-ray beam propagates
(a) in the [010] direction and has a wavelength of 2.08 nm
(b) in the [120] direction and has a wavelength of 2.28 nm
Hint: Please solve the problem graphically. The first part of the problem can be solved by drawing only the reciprocal lattice. For the second part of the problem the real lattice as well as the reciprocal lattices have to be drawn, for simplification use the same origin for both lattices.
4.16 Explain how this LEED pattern could be used to determine the 2D Bravais lattice of atoms at a surface.

4.17 (a) Explain the difference between powder diffraction and x-ray diffraction on single crystals.
(b) A powder of a crystalline material is investigated by x-ray powder diffraction using a wavelength of 0.229 nm. The crystalline material has a tetragonal crystal structure with lattice constants $a =$ 0.25 nm and $c =$ 0.3 nm. At which angles $2\theta$ are diffraction peaks expected?
4.18 (Old exam question) This image shows the CsCl crystal structure. The lattice parameters of the conventional unit cell are given in the figure.
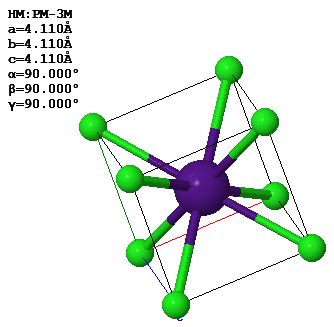
(a) What is the closest distance between a Cs atom and a Cl atom?
(b) Draw the (110) plane of CsCl.
(c) What are the primitive lattice vectors in reciprocal space?
$\vec{b}_1=$
$\vec{b}_2=$
$\vec{b}_3=$
(d) What is the length of the reciprocal lattice vector $\vec{G}_{111}$?
The atomic form factors for Cs and Cl are:
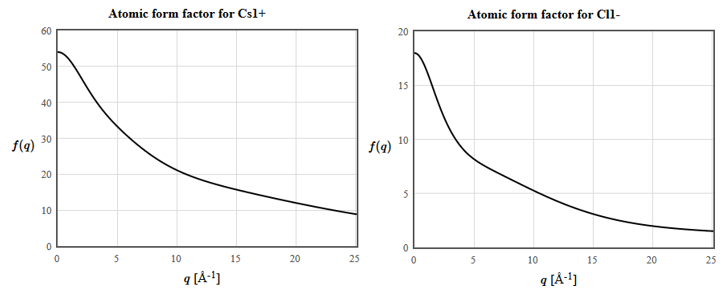
(e) The horizontal axis is the scattering vector $\vec{q}= \vec{k}'-\vec{k}$. What is the structure factor of $\vec{G}_{111}$?