PHY.K02UF Molecular and Solid State Physics
|
| ||||
PHY.K02UF Molecular and Solid State Physics | ||||
In a crystal, atoms are arranged in straight rows in a three-dimensional periodic pattern. A small part of the crystal that can be repeated to form the entire crystal is called a unit cell.
|
|
|
|
A crystal can be specified in several ways. One way is to repeat the primitive unit cell at each translation vector,
$$\vec{T} = h\vec{a}_1 + k\vec{a}_2 + l\vec{a}_3$$Here $\vec{a}_1$, $\vec{a}_2$, $\vec{a}_3$ are the primitive lattice vectors and $h$, $k$, and $l$ are integers. The primitive lattice vectors are not unique; different choices for the primitive lattice vectors are possible.
Another common way to specify crystal is to give the lattice parameters $(a,b,c,\alpha,\beta,\gamma )$, the space group, and the asymmetric unit. The lattice parameters $a$, $b$, and $c$ are the lengths of the sides of a parallelepiped; $\alpha$ is the angle between $b$ and $c$; $\beta$ is the angle between $a$ and $c$; and $\gamma$ is the angle between $a$ and $b$. This parallelepiped can have a larger volume than the primitive unit cell. If it is possible to use a cubic unit cell, crystalographers use the smallest possible cube as the conventional unit cell. For simple cubic, the conventional unit cell is the primitive unit cell but for bcc, the conventional unit cell is twice the volume of the primitive unit cell and for fcc, the conventional unit cell has four times the volume of the primitive unit cell. The asymmetric unit is the minimum number of atoms you need to specify to create the basis by applying the symmetries of the space group to the asymmetric unit.
The lattice parameters, conventional unit cells, and primitive unit cell of some common crystal structures are linked below.
3.1 Explain what a Bravais lattice is and what a basis is. How can you construct the basis from the asymmetric unit?
3.2 Calcium Fluoride, CaF2, has an fcc Bravais lattice and a basis with Ca at 000 and F's at fractional coordinantes ¼ ¼ ¼ and ¾ ¾ ¾ of the conventional (cubic) unit cell. Sketch one conventional (cubic) unit cell of the structure. Sketch a primitive unit cell. The lattice constant is $a = $ 5.451 Å. What is the distance from a Ca to an F atom in Angstroms?
3.3 Graphene is a two-dimensional lattice which is built by a continuous arrangement of regular hexagons of sp² hybridized carbon atoms (see below). The distance between nearest neighbor atoms is 0.14 nm.
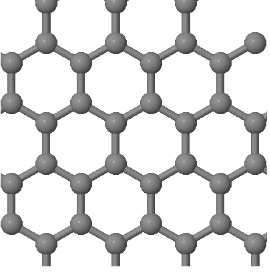
(a) What is the Bravais lattice of graphene?
(b) Draw the Wigner-Seitz primitive unit cell.
(c) How many atoms are there in a primitive unit cell?
(d) Determine the basis vectors that describe the postions of the atoms in the unit cell. Write these basis vectors first in terms of the absolute positions (with x- and y- components and distances in Angstroms) and then in fractional coordinates. For fractional coordiantes give the positions in terms of the conventional lattice vectors. The conventional lattice vectors are the same as the primitive lattice vectors in this case.
3.4 The space group of a crystal is 227. How can you determine the point group and the Bravais lattice of this crystal?
3.5 The conventional unit cell and lattice parameters of graphite are shown below.
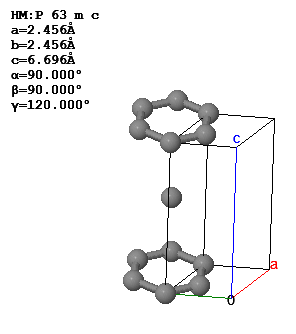
What is the Bravais lattice, the basis, the primitive lattice vectors, and the volume of the primitive unit cell?
3.6 A conventional (cubic) unit cell of zincblende, ZnS, is shown below. Note the similarity to the diamond structure.
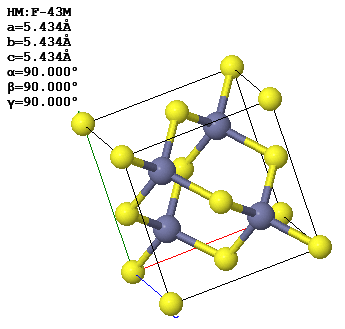
(a) How many atoms of each type are contained in a conventional unit cell?
(b) What is the Bravais lattice?
(c) Give a set of fundamental translation vectors $(\vec{a}_1, \vec{a}_2, \vec{a}_3)$ which can be used to define the primitive unit cell. How many atoms are there in the primitive cell?
3.7 A two dimensional crystal is shown below.

(a) Draw a unit cell indicating the two primitive lattice vectors in this plane. How many atoms are there in the primitive unit cell?
(b) Draw the two dimensional Bravais lattice.
3.8 Polonium forms a simple cubic crystal with one atom in the basis. The lattice constant is 3.359 Å.
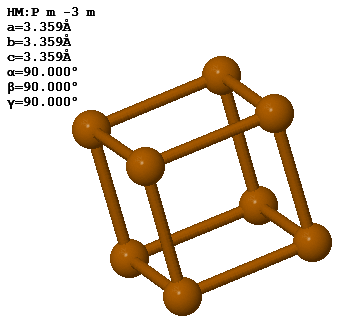
The density of Po is 9.23 g/cm³. How many unit cells are there in 100 g of polonium?
3.9 For an hcp crystal: $a=b=c/1.633$, $\alpha=90^{\circ}$, $\beta=90^{\circ}$, $\gamma=120^{\circ}$. Calculate the volume of the primitive unit cell in terms of $a$.
3.10 Show for an ideal hcp structure that ratio $c/a$ is
\[ \begin{equation} \frac{c}{a}=\sqrt{\frac{8}{3}}=1.633. \end{equation} \]3.11 There are four orthorhombic Bravais lattices but only two tetragonal Bravais lattices.
(a) Show that a base-centered (C) tetragonal lattice is equivalent to a primitive (P) tetragonal lattice.
(b) Show that a face-centered (F) tetragonal lattice is equivalent to a body-centered (I) tetragonal lattice.
3.12 Draw the following crystal structures: simple cubic, fcc, bcc, NaCl, CsCl, hexagonal, tetragonal, and orthorhombic.
3.13 Show that the maximum proportion of the available volume which can be filled by hard spheres arranged on various lattices is: simple cubic, 0.52; body-centered cubic, 0.68; face-centered cubic, 0.74.
Miller indices
Every point of a Bravais lattice can be reached from the origin by a translation vector of the form,
where $\vec{a}_1$, $\vec{a}_2$, $\vec{a}_3$ are the primitive lattice vectors and $h$, $k$, and $l$ are integers called the Miller indices. The direction that the vector $\vec{T}_{hkl}$ points is denoted with square brackets, $[hkl]$. If there are directions that are equivalent due to symmetry any of the equivalent directions are specified by angular brackets <$hkl$>.
For example, in a cubic system:
<100> = [100], [010], [001], [-100], [0-10], [00-1]
<110> = [110], [-1-10], [1-10], [-110], [101], [-10-1], [-101], [10-1], [011], [0-1-1], [0-11], [01-1].
Often the minus signs are drawn as overlines [-10-1] = $\left[\overline{1}0\overline{1}\right]$. This is pronounced one-bar zero one-bar.
Planes
Using Miller indices, planes are denoted with curved brackets $(hkl)$. The $(hkl)$ plane intercepts the axis in the direction of $\vec{a}_1$ at $\frac{|\vec{a}_1|}{h}$, the axis in the direction of $\vec{a}_2$ at $\frac{|\vec{a}_2|}{k}$, and the axis in the direction of $\vec{a}_3$ at $\frac{|\vec{a}_3|}{l}$.
Equivalent planes are denoted with curly brackets $\{hkl\}$. Three points that can be used to define the $(hkl)$ plane are $\left( \frac{a_{1x}}{h},\frac{a_{1y}}{h},\frac{a_{1z}}{h} \right)$, $\left(\frac{a_{2x}}{k},\frac{a_{2y}}{k},\frac{a_{2z}}{k} \right)$, and $\left(\frac{a_{3x}}{l},\frac{a_{3y}}{l},\frac{a_{3z}}{l}\right)$. The normal vector to this plane can be determined by taking the cross product of two vectors in the plane. If $(h,k,l \ne 0)$, two suitable vectors are $\vec{v}_1=\frac{\vec{a}_1}{h}-\frac{\vec{a}_3}{l}$ and $\vec{v}_2=\frac{\vec{a}_2}{k}-\frac{\vec{a}_3}{l}$. The unit vector normal to the $(hkl)$ plane is,
$$\hat{n}_{hkl}=\frac{\vec{v}_1\times \vec{v}_2}{|\vec{v}_1\times \vec{v}_2|}.$$For cubic crystals, $\vec{T}_{hkl}$ is normal to $(hkl)$ and parallel to $\hat{n}_{hkl}$ but this is not generally true for crystals with other symmetries.
3.14 Equivalent planes and directions.
(a) which planes are equivalent to (100) in a tetragonal system?
(b) which planes are equivalent to (210) in a tetragonal system?
(c) which directions are equivalent to [120] in a tetragonal system?
3.15 (a) The lattice parameters of a tetragonal crystal are $a = b = 2$ Å, $c = 3$ Å, $\alpha = \beta = \gamma = 90^{\circ}$. From this information we can deduce that the primitve lattice vectors are $\vec{a}_1 = a\,\hat{x}$, $\vec{a}_2 = a\,\hat{y}$, and $\vec{a}_3 = c\,\hat{z}$. What is the length of the translation vector $\vec{T} = 2\vec{a}_1 + 6\vec{a}_2 + 5\vec{a}_3$? What is the unit vector that points in the direction of $\vec{T}$? What are the Miller indices that specify this direction in the crystal?
(b) The lattice parameters of a simple hexagonal crystal are $a = b = 3$ Å, $c = 4$ Å, $\alpha = \beta = 90^{\circ}$, $\gamma = 120^{\circ}$. From this information determine the primitive lattice vectors. What is the length of the translation vector with $h = 4$, $k = 3$, and $l = 1$ ?
3.16 Draw the (111) and (222) planes in a simple cubic unit cell, with lattice constant $a$. Determine the normal distance between the two planes.
3.17 Draw the NaCl crystal structure. What is the Bravais lattice? What shape does the Wigner-Seitz cell have? What are the positions of the atoms of the basis given in fractional coordinates of the conventional (cubic) unit cell? Draw a (111) plane.
3.18 Calculate the angle between the [110] direction and the [111] direction for a monoclinic lattice with a = 0.3 nm, b = 0.4 nm, c = 0.5 nm, and β = 107°.
3.19 A metal has an fcc crystal structure. The lattice constant is 0.38 nm and the atomic weight of the atoms is 85. The lattice constant is the length of the conventional (cubic) unit cell. The mass of an atom is the atomic weight times the atomic mass constant $u$ = 1.6605402 × 10-27 kg.
a) What is the density of this metal?
b) What is the distance between neighboring atoms?
c) The metal is cut so that the (111) is exposed on the surface. Draw the arrangement of atoms you would see if you looked at this surface. Label the two directions in the (111) plane.
3.20 A bcc crystal is cut so that the (011) plane is exposed on the surface. Draw the arrangement of atoms on the crystal surface. How could you determine the pattern of the atoms on the surface of a metal experimentally?
The set of planes perpendicular to a vector \(A_x\hat{x}+A_y\hat{y}+A_z\hat{z}\) is,
$$A_xx+A_yy+A_zz = C,$$where \(C\) is any constant. If a point \( (x_0,y_0,z_0)\) on the plane is known, \(C\) can be calculated,
$$C=A_xx_0+A_yy_0+A_zz_0.$$The app below will solve 3 linear equations for three unknowns. (It determines the point where three planes intersect.)
3.21 The faces of a Wigner-Seitz cell are defined by planes that perpendicularly bisect vectors from the origin to the Bravais lattice points. To determine where the corners of a Wigner-Seitz cell are, it is necessary to find the points where three planes intersect. For an bcc lattice, the primitive lattice vectors are,
$\vec{a}_1=\frac{a}{2}(\hat{x}+\hat{y}-\hat{z}),\quad \vec{a}_2=\frac{a}{2}(-\hat{x}+\hat{y}+\hat{z}),\quad\vec{a}_3=\frac{a}{2}(\hat{x}-\hat{y}+\hat{z})$.
Here $a$ is the length of a side of the conventional cubic unit cell. At which point do the planes that bisect the vectors $\vec{a}_1$, $\vec{a}_2$, and $\vec{a}_3$ meet?
3.22 Miller Indices $hkl$ denote a specific plane in a Bravais lattice, as notation of a plane the Miller indices are given in round brackets. Please note that the three Miller indices are coprime (teilerfremd). This means that the plane intersects points of the Bravais lattice. An example of the (623) plane is shown below.
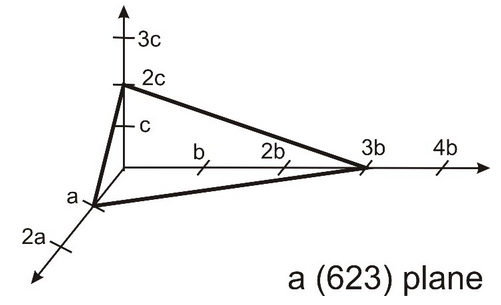
(a) Draw the (313) plane.
(b) Draw the (340) plane.
3.23. A plane cuts the crystalographic axes of a crystal at $3\vec{a}$, $4\vec{b}$, and $6\vec{c}$ where $\vec{a}$, $\vec{b}$, and $\vec{c}$ are the primitive lattice vectors. What are the Miller indices of this plane?
3.24 Draw the Wigner-Seitz cells of the following lattices:
In two dimensions, a Bravais lattice has two primitive lattice vectors \(\vec{a}\) and \(\vec{b}\). The lengths of these vectors are the lattice constants \(a\) and \(b\).The angle between the primitive lattice vectors is \(\gamma\). There are five two-dimensional Bravais lattices,
If more than one Bravais lattice can be used to describe a periodic structure, there are priority rules to determine the 2D Bravais lattices.
3.25 In a Cairo tiling, a two-dimensional plane is fully filled by pentagons. The geometry of a single pentagon is formed by four identical side length (blue) and one different side length (red) and angles of 90° and 120°.
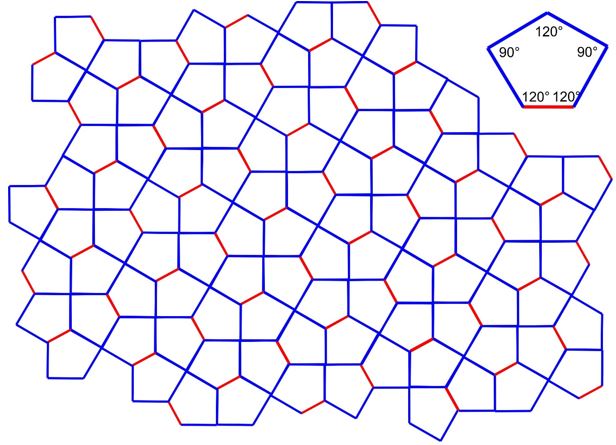
(a) Determine the 2D Bravais lattice of the Cairo tiling.
(b) Draw the unit cell vectors \(\vec{a}\) and \(\vec{b}\) and the enclosed angle \(\gamma\).
(c) Determine \(\gamma\).
(d) How many tiles are within one unit cell?
3.26 A triangle-hexagon tiling covers a two-dimensional plane with equilateral triangles and hexagons. Two different lengths are involved (drawn in blue and red) with a ratio of 3:2. The arrangement of the tiles is given in the drawing below.
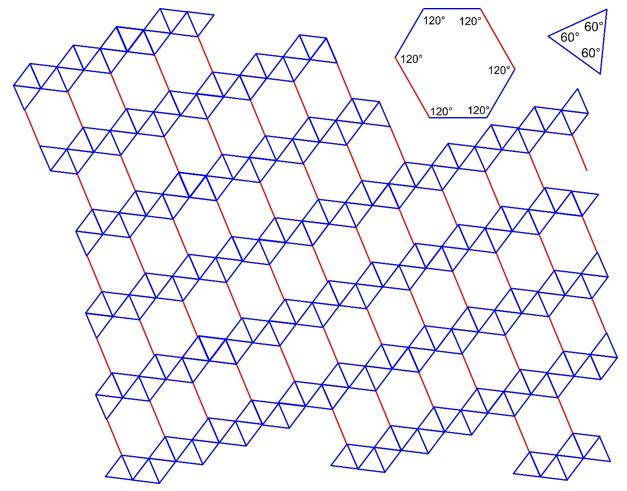
(a) Determine the 2D Bravais lattice of the tiling.
(b) Draw Bravais lattice points.
(c) Draw the unit cell vectors \(\vec{a}\) and \(\vec{b}\) and the enclosed angle \(\gamma\).
(d) How many triangles and how many hexagons are there in a unit cell?
(e) How many triangles and how many hexagons are associated with one Bravais lattice point?
3.27 In case of a hexagonal lattice $(a = b \ne c,\, \alpha = \beta = 90^{\circ}, \,\gamma = 120^{\circ})$ four Miller indices $(hkil)$ are used to give the notation of a crystallographic plane. The Miller index $i$ is given by $i = -h-k$. The use of the index $i$ simplifies the identification of equivalent planes (equivalent planes are planes with identical interplanar distance $d_{hkl}$ of the hexagonal lattice, since cyclic permutation of the indices $hki$ within $(hkil)$ gives equivalent planes.
Show graphically all equivalent planes to (11-20).
3.28 Poles are directions perpendicular to a crystallographic plane
Consider an orthorhombic lattice with lattice constants $a = 3$ Å, $b = 4$ Å, $c = 5$ Å. Give the (approximate) pole direction of the (210) plane, which is the crystallographic direction [uvw] oriented perpendicular to the (210) plane.
Comment:
This problem can be solved graphically, a graphical solution is more difficult for a general plane like (213).
3.29 Consider a cubic lattice. Give a single crystallographic direction [uvw] which is within the (111) plane. Note, there many directions within the (111) plane.
A more difficult problem is: Consider a triclinic lattice. Give all crystallographic directions [uvw] which are within the (111) plane.