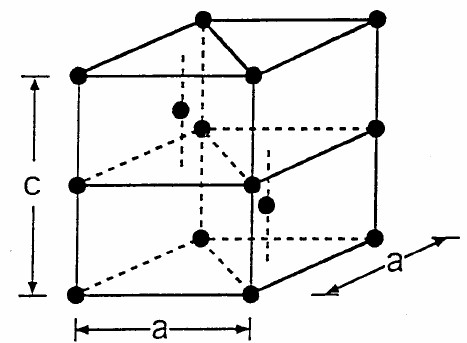
The figure below shows a primitive unit cell of one crystalline form of the element americium. The space lattice is hexagonal with $\vec{a}_1 = a\hat{x}, \vec{a}_2 =1/2a\hat{x} +1/2\sqrt{3}a\hat{y}, ~and~ \vec{a}_3 = c\hat{z}$. The basis is (0 0 0) , (2/3 2/3 1/4), (0 0 1/2) and (1/3 1/3 3/4).

(a) At first we want to calculate reciprocal lattice vectors \(\vec{b}_1,\vec{b}_2,\vec{b}_3\). The vectors are defined as follows:
\[ \begin{equation} \vec{b_1}=2\pi \dfrac{a_2 \times a_3}{a_1 (a_2 \times a_3)} \\ \vec{b_2}=2\pi \dfrac{a_3 \times a_1}{a_1 (a_2 \times a_3)} \\ \vec{b_3}=2\pi \dfrac{a_1 \times a_2}{a_1 (a_2 \times a_3)} \end{equation} \]With the given values of \(\vec{a_i}\) we get:
\begin{align} \vec{b_1}&=\dfrac{2\pi}{\sqrt{3}a} \begin{pmatrix} \sqrt{3}\\-1\\0 \end{pmatrix}\\ \vec{b_2}&=\dfrac{4\pi}{\sqrt{3}a} \begin{pmatrix} 0\\1\\0 \end{pmatrix}\\ \vec{b_3}&=\dfrac{2\pi}{c} \begin{pmatrix} 0\\0\\1 \end{pmatrix} \end{align}The reciprocal lattice vector is defined as follows:
\begin{align} \vec{G}=h \vec{b_1}+k \vec{b_2}+ l \vec{b_3} \end{align}Where the integers $h,k,l$ label the reciprocal lattice points. The reciprocal lattice is hexagonal.

Fig. 1: 2D Sketch of a hexagonal reciprocal lattice
In Figure 1, sketch of the reciprocal lattice in the $\vec{b}_1$ - $\vec{b}_2$ plane is shown. The vector \(\vec{b_3}\) is normal to this plane. The lattice in 3D consists of more layers spaced a distance $\frac{2\pi}{c}$ apart.
(b)
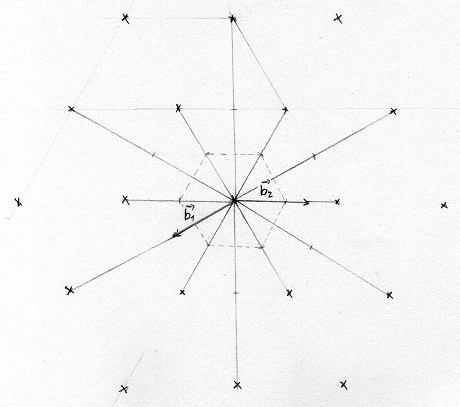
Fig 2: 2D Sketch of a hexagonal reciprocal lattice with Brillouin Zone drawn as a dotted line
In figure 2 we can see the drawn Brillouin Zone in the middle, the length from the center to each corner is \(\frac{4\pi}{3a}\) the height of the 3D Brillouin Zone is \(\frac{2\pi}{c}\). The structure of the Brillouin Zone is also hexagonal.
(c) The structure factors are given by
\begin{align} n_{\vec{G}}=\sum\limits_{j}f_j(\vec{G})e^{-i\vec{G}\cdot \vec{r_j}} \end{align}where $f_j(G)$ are the atomic form factors and $j$ sums over the atoms in the basis. From this point there are two ways to proceed. Either we look up the atomic form factors for americium or we assume that the electron density of an atom can be described by \(Z\delta(\vec{r})\), where $Z=95$ is the atomic number of americium. In the $\delta$-function approximation, the atomic form factor is 95 for all $G$.
We use equation 6 to calculate the structure factor, the \(r_j\) are the bases given. The calculation for the 100 reflection goes as follows:
\begin{align} n_{\vec{G}_{100}}&=\sum\limits_{j}Z\delta(\vec{r}-\vec{r_j})e^{-i\vec{G}_{100}\cdot \vec{r_j}}\\ &=Ze^{-2\pi i 0}+Ze^{-2\pi i \frac{2}{3}}+Ze^{-2\pi i 0}+Ze^{-2\pi i \frac{1}{3}}\\ &=95(1-0.5-0.866i+1-0.5+0.866i)\\ n_{\vec{G}_{100}}&=95 \end{align}For the two other planes the calculation goes the same way:
\begin{align} n_{\vec{G}_{001}}&=\sum\limits_{j}Z\delta(\vec{r}-\vec{r_j})e^{-i\vec{G}_{001}\cdot \vec{r_j}}\\ &=Ze^{-2\pi i 0}+Ze^{-i\frac{\pi}{2}}+Ze^{-\pi i 0}+Ze^{-i\frac{3\pi}{4}}\\ n_{\vec{G}_{001}}&=0 \end{align} \begin{align} n_{\vec{G}_{120}}&=\sum\limits_{j}Z\delta(\vec{r}-\vec{r_j})e^{-i\vec{G}_{120}\cdot \vec{r_j}}\\ &=Ze^{-2\pi i 0}+Ze^{-4\pi i}+Ze^{-2\pi i 0}+Ze^{-2\pi i }\\ n_{\vec{G}_{120}}&=380 \end{align}We can also look up the atomic form factors in the International Tables for Crystallography: http://it.iucr.org/Cb/ch6o1v0001/. The values given in the tables are plotted at: http://lampz.tugraz.at/~hadley/ss1/crystaldiffraction/atomicformfactors/formfactors.php
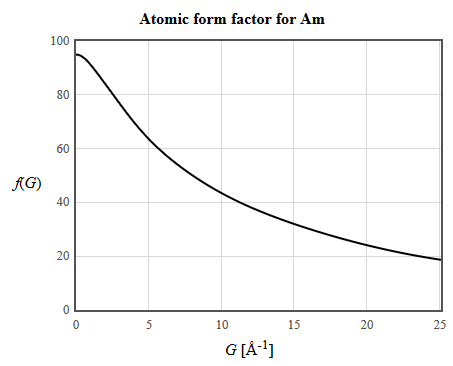
For the 100 reflection, $|G|=2.092$ Å-1 and $f(G) = 83.46$. For the 001 reflection, $|G|=0.559$ Å-1 and $f(G) = 93.65$. For the 120 reflection, $|G|=3.624$ Å-1 and $f(G) = 72.32$. Using equation 6 results in the structure factors,
\begin{align} n_{\vec{G}_{100}}&=83.46 \\ n_{\vec{G}_{120}}&=0 \\ n_{\vec{G}_{120}}&=289.3 \end{align}This can be checked by using the app at http://lampz.tugraz.at/~hadley/ss1/crystaldiffraction/atomicformfactors/structurefactor.php and the lattice constants $a=3.468$ Å and $c=11.24$ Å.
(d) The scattering intensity is the square of the form factors, so the ratio is:
\begin{align} \dfrac{|n_{\vec{G}_{120}}|^2}{|n_{\vec{G}_{100}}|^2}=16, \end{align}using the $\delta$-function approximation and,
\begin{align} \dfrac{|n_{\vec{G}_{120}}|^2}{|n_{\vec{G}_{100}}|^2}=12, \end{align}using the International Tables for Crystallography.
This problem is complicated enough that it is useful to calculate it using both the $\delta$-function approximation and the online app. Although the app should give the right answer, it requires that you input a lot of information and you may make a typing mistake. It is easy enough to check the result by hand using the $\delta$-function approximation. You can also make the primitive lattice vectors a factor of 10 or 100 too large in the app. This makes the reciprocal lattice vectors smaller and the app should then give the same answer as the $\delta$-function approximation.
Philip Zettl