Problem 1
(a) Which Hamiltonian is solved exactly by a product of atomic orbitals? Write down this Hamiltonian. How do you calculate the energy of a product of atomic orbitals evaluated with this Hamiltonian?
(b) What is a molecular orbital? How do you determine how many molecular orbitals are needed to describe a molecule?
(c)How do you decide how many atomic orbitals are needed to describe a molecular orbital when using the Linear Combination of Atomic Orbitals?
(d) If you know how the atoms are arranged in a molecule, which of the following (Electronic energy levels, Vibrational energy levels, Rotational energy levels) can you determine without solving the Schrödinger equation? Explain your reasoning.
(e) What is the exchange energy?
Problem 2
A crystal has an face centered cubic Bravais lattice and there are three atoms in the basis. The lattice constant of the conventional unit cell is 2 Å.
(a) How many atoms are there in a conventional unit cell?
(b) How many $k$-states are there for every conventional unit cell?
(c) How many optical phonon branches does this crystal have?
(d) What are the primitive lattice vectors?
$\vec{a}_1 = $
$\vec{a}_2 = $
$\vec{a}_3 = $
(e) What is the point on the first Brillouin zone boundary that is closest to the $\Gamma$ point?
Problem 3
GaN has a hexagonal Bravais lattice with 4 atoms in the basis. The reciprocal lattice of a hexagonal lattice is also hexagonal. For GaN, the primitive reciprocal lattice vectors are,
$$\vec{b}_1 = 1.97 \hat{k}_x - 1.137 \hat{k}_y\text{ A}^{-1},\qquad\vec{b}_2 = 1.97 \hat{k}_x + 1.137 \hat{k}_y\text{ A}^{-1},\qquad\vec{b}_3 = 1.12 \hat{k}_z\text{ A}^{-1}$$(a) A powder diffraction experiment is performed with x-rays with a wavelength of 1 Å. At which angle $2\theta$ is the 111 diffraction peak observed?
(b) GaN has a direct band gap of 3.4 eV and the electrons have a lighter effective mass than the holes. Plot the electronic density of states of GaN. Draw the position of the chemical potential at $T=0$ K into the plot.
(c) What wavelengths of light does GaN absorb?
(d) What properties must GaN have for it to be piezoelectric?
$\hbar = 1.05457266\times 10^{-34}$ J s, $e= 1.60217733\times 10^{-19}$ C, $c = 2.99792458\times 10^8$ m/s
Problem 4
The density of states of a material is shown below. The dashed red lines indicate where the Fermi energy would be if there were 1 electron/unit cell, 2 electrons/unit cell, etc.
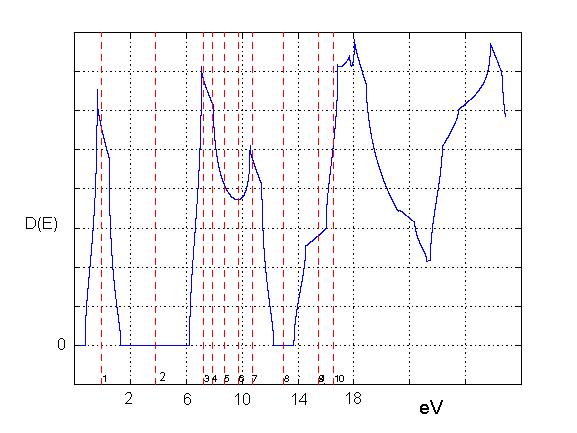
(a) State the type of type of material (metal, insulator, semiconductor).