PHY.K03 Solid State Physics - 30.06.2025

All subquestions a, b, c, $\cdots$ are worth 5 points.

Problem 1

Consider a CO₂ molecule. A section of the periodic table of atomic masses is shown to the right.

(a) How many rotational and vibrational modes does CO₂ have?

(b) CO₂ is prepared with ¹²C and ¹³C isotopes. The isotope of oxygen is always ¹⁶O. How do the rotational and vibrational frequencies compare between the molecules with ¹²C and the molecules with ¹³C?

(d) How many occupied molecular orbitals are there in the ground state of a CO₂ molecule? How many are occupied in the first excited state of a CO₂ molecule?

Solution

<hr />
(a) Linear molecules: 2 rotational modes, $3N - 5$ vibrational modes ($N$ is the number of atoms) 
Nonlinear molecules: 3 rotational modes, $3N - 6$ vibrational modes
CO2 is linear: 2 rotational, 4 vibrational modes.

(b) Since the carbon atom is at the center of mass, the rotational modes won't be affected. In any vibrational mode where the carbon atom moves, molecules with a 13C isotope will have a lower frequency. In the symmetric stretch mode, the carbon atom does not move, so the frequency won't change, but in the other three vibrational modes, it does move.

(c) The Bose-Einstein factor predicts the mean number of bosons in a state with energy $E$.

$$\frac{1}{\exp\left(\frac{E-\mu}{k_BT}\right) -1}$$

or you can say that the ratio of the occupation probabilities of state $j$ to state $i$ is given by a Boltzmann factor,

$$\frac{P_j}{P_i} = \frac{g_j\exp\left(\frac{-E_j}{k_BT}\right)}{g_i\exp\left(\frac{-E_i}{k_BT}\right)}$$

where $g_i$ is the degeneracy of state $i$.

(d) There are 2 × 8 electrons in the oxygen atoms, and 6 electrons in the carbon atom, yielding a total of 22 electrons which would fill 11 molecular orbitals in the ground state. In the first excited state, one electron would be promoted to a higher orbital, so there would be 10 doubly occupied molecular orbitals and two singly occupied molecular orbitals.

See exercise questions: 2.3, 2.10, 2.19, 2.20, 2.23, 2.25, 2.26, 2.27

<hr />

Problem 2
The conventional unit cell of solid CO₂ (dry ice) is shown below.

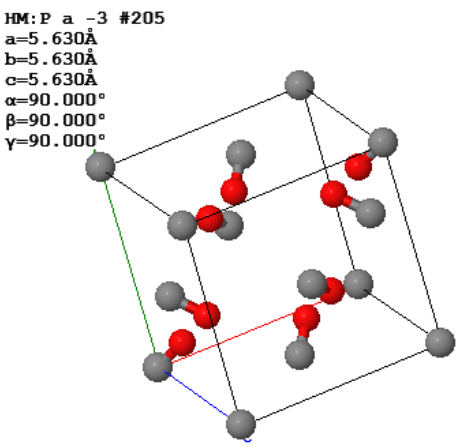All of the oxygen atoms (red) are entirely within the conventional unit cell. All of the carbon atoms (gray) are either in the corners or on the faces.

(a) What is the Bravais lattice of this crystal?

(b) What is the smallest value of $2\theta$ in a diffraction experiment of dry ice if the x-rays have a wavelength of 1.54 Å?

$$2\theta = $$

(d) The electronic band structure of dry ice is shown below. At zero temperature, the states are occupied up to $E=0$.

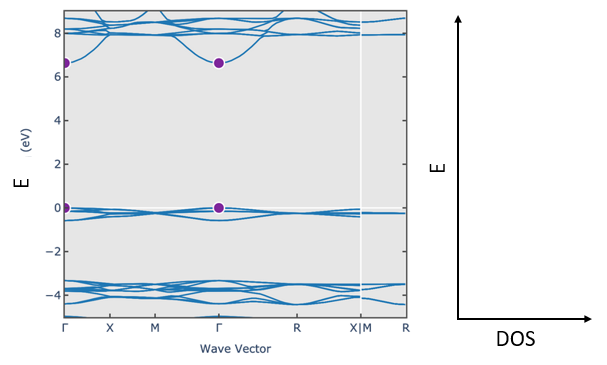
Draw the electron density of states. Is this a metal, a semiconductor, or an insulator? Why? Draw the position of the chemical potential at room temperature.

Solution

<hr />
(a) The Bravais lattice is simple cubic. The carbons are on the fcc sites, but the arrangements of the oxygens are not the same around every carbon atom. The space group of a crystal uniquely determines the Bravais lattice and the point group. The space group was given as Pa$\overline{3}$ #205 and the table says the Bravais lattice is simple cubic.

(b) The smallest angle corresponds to the shortest reciprocal lattice vector $=|\vec{G}_{100}| = \frac{2\pi}{5.63}$ Å
-1.

$$\sin\theta = \frac{|\vec{G}_{100}|}{2k}$$

$$2\theta = 0.274 \text{ rad  }= 15.72\text{ deg.}$$

(c) There are 8 oxygen atoms and 4 carbon atoms in the primitive unit cell, so there are 3 acoustic modes and 33 optical modes.

(d) This is an insulator, the band gap is larger than 6 eV. The chemical potential of an insulator is in the middle of the band gap.

See exercise questions: 3.1, 3.10, 5.3, 5.10, 5.15, 5.16, 5.18, 5.22, 7.2, 7.8, 7.14, 7.18, 9.4, 9.11, 9.15, 9.17

<hr />

Problem 3
Gold has an fcc crystal structure where the lattice constant of the conventional unit cell is, $a=4.079$ Å. Gold is monovalent, and the effective mass of the electrons is $1.26\,m_e$ where $m_e$ is the mass of a free electron.

(a) How could the lattice constant be measured experimentally?

(b) How could the effective mass be measured experimentally and/or calculated theoretically?

(d) If you wanted to improve your calculations of the properties of gold, what additional information would you need?

Solution

<hr />
(a) The lattice constant could be measured with x-ray diffraction.

(b) Within the free electron model, the effective mass is related to all of the thermodynamic properties. It can be fit using a specific heat measurement or a bulk modulus measurement. The effective mass can be calculated from the band structure by examining the curvature of the bands. ARPES could also be used to measure the curvature of the bands. For a metal where the chemical potential cuts many bands, you could look at the Fermi energy which contains the effective mass in the free-electron model.

(c) The electron contribution to any equilibrium thermodynamic property can be calculated (there is also a phonon contribution). Properties that can be calcualted include the electron density, the chemical potential, internal energy, specific heat, entropy, bulk modulus, Helmholtz free energy, etc.,

(d) Rather than the effective mass, the density of states at the Fermi energy and the derivative of the density of states at the Fermi energy could be used in the Sommerfeld model. A better approach would be to use a band structure calculation. Everything you can know about a solid is contained in the solutions to the Schrödinger equation for the crystal, and this is a band structure calculation.

See exercise questions: 8.5, 8.6, 8.7, 8.11, 8.12
<hr />