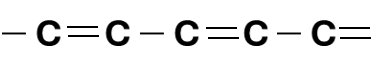
Problem 1

Assume a linear chain (1D) of carbon atoms ($m_C = 19.926 \times 10^{-27}$ kg), with a carbon-carbon distance of 3Å between all carbon atoms and a force constant of $6.5 \times 10^{-7}$ N/nm.

1. Draw the dispersion relation (frequency versus $k$) and the phonon density of states for this system (30% of the points)
2. What is the energy (in eV) of the phonon with the largest frequency in this system? (40% of the points)
3. Sound waves that we can hear are at low frequencies (near $\vec{k}=0$). The speed of sound is $c = \lambda f$, where $\lambda$ is the wavelength and $f$ is the frequency of the waves. What is the speed of sound in this system? (10% of the points)
4. Instead of the above-described linear chain, consider polyacetylene instead, a chain consisting of alternating single and double bonds (see below), i.e. with two atoms in the unit cell. Draw the dispersion relation and the phonon density of states for the system (under the assumption that the carbon-carbon distance is still 3 Å and the two force constants are nearly the same as in the above system). (20% of the points)

   

Solution

Problem 2
A bivalent metal has a body-centered cubic (BCC) Bravais lattice with a lattice constant of $a = 0.15$  nm. Using surface science techniques, we synthesize a single layer of this material on an insulating substrate, replicating the atomic arrangement of its (110) crystallographic plane. Assume that there is no charge transfer at the interface and the two-dimensional electron gas model can be employed.

1. Calculate the surface electron density $n$ [1/m²] (20% of the points)
2. Draw the top view of the surface plane. Draw a primitive unit cell. Which is the 2D Bravais lattice of the primitive unit cell of the surface plane? (25% of the points)
3. Knowing that the expression of the DOS (per unit area) for a 2D electron gas is: $\frac{D(E)}{A}=\frac{m_e}{\pi\hbar^2}$ [J^-1 m^-2] derive an analytic expression for the surface electron density (25% of the points)
4. Calculate the Fermi energy in eV (15% of the points)
5. Calculate the Hall coefficient (15% of the points)

Solution

Problem 3
This is the trial wave function for benzene: \[ \begin{equation} \psi_{\text{mo,j}}(\vec{r})=\frac{1}{\sqrt{6}} \sum_{n=1}^{6} e^{\frac{i2\pi n j}{6}}\phi_{2p_z}^C(\vec{r}-\vec{R}_n) \end{equation} \]

1. Generalize the trial wave function for a linear chain of length $L$, consisting of $N$ carbon atoms, with a spacing $a$ between atoms. (30% of the points)
2. Assuming that the linear chain satisfies the Periodic Boundary Conditions (PBC), express the trial wave function as a function of $k$. (30% of the points)
3. Prove that the following function: \[ \begin{equation} \psi_{\vec{k}}(\vec{r})=\frac{1}{\sqrt{N}} \sum_{\vec{R}} e^{i\vec{k}\cdot\vec{R}}\phi(\vec{r}-\vec{R}) \end{equation} \] which is the ansatz used in the tight binding model, is an eigenfunction of the translation operator. (40% of the points)

Solution