First name
Last name
Matrikelnr.
Problem 1
The many-particle Hamltonian for any molecule is,
\[ \begin{equation} \label{eq:htotal} H_{\text{mp}}= -\sum\limits_{i=1,2} \frac{\hbar^2}{2m_e}\nabla^2_i -\sum\limits_a \frac{\hbar^2}{2m_a}\nabla^2_a -\sum\limits_{a,i} \frac{Z_ae^2}{4\pi\epsilon_0 |\vec{r}_i-\vec{r}_a|}+\sum\limits_{i< j} \frac{e^2}{4\pi\epsilon_0 |\vec{r}_i-\vec{r}_j|}+\sum\limits_{a< b} \frac{Z_aZ_be^2}{4\pi\epsilon_0 |\vec{r}_a-\vec{r}_b|} . \end{equation} \]We apply the Born-Oppenheimer approximation and write the electronic Hamiltonian $H_{\text{elec}}$ as,
\[ \begin{equation} \label{eq:helec} H_{\text{elec}}= -\sum\limits_i \frac{\hbar^2}{2m_e}\nabla^2_i -\sum\limits_{a,i} \frac{Z_ae^2}{4\pi\epsilon_0 |\vec{r}_i-\vec{r}_a|}+\sum\limits_{i< j} \frac{e^2}{4\pi\epsilon_0 |\vec{r}_i-\vec{r}_j|} +\sum\limits_{a< b} \frac{Z_aZ_be^2}{4\pi\epsilon_0 |\vec{r}_a-\vec{r}_b|}. \end{equation} \]This Hamiltonian has no simple solution. To describe molecular hydrogen H2, Heitler and London associated an each electron to an atom and neglected the electron-electron interactions and the interactions between electron and the nuclei of other atoms. The resulting Hamiltonian is a sum of atomic Hamiltonians,
\[ \begin{equation} \label{eq:helecred} H_{\text{vb}}= - \frac{\hbar^2}{2m_e}\nabla^2_1 - \frac{\hbar^2}{2m_e}\nabla^2_2- \frac{e^2}{4\pi\epsilon_0 |\vec{r}_1-\vec{r}_{a}|}- \frac{e^2}{4\pi\epsilon_0 |\vec{r}_2-\vec{r}_{b}|}= \sum\limits_i H_{\text{atom}_i}. \end{equation} \](a) It is possible to find exact antisymmetric two-electron wavefunctions that are eigenstates of $H_{\text{vb}}$. What is the ground state wave function?
(b) The first excited state of $H_{\text{vb}}$ splits into a singlet state and a triplet state. Write down the singlet state wavefunction and the triplet state wavefunction.
(c) How could you use the eigenstates of $H_{\text{vb}}$ to calculate the bond potential for H2?
First name
Last name
Matrikelnr.
Problem 2
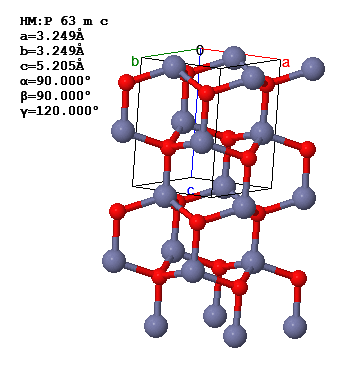
ZnO in the wurzite structure is shown below.

There are two atoms in the asymmetric unit and four atoms in the primitive unit cell.
(a) What is the Bravais lattice of ZnO?
(b) Consider the symmetry element described by the matrix, \begin{equation} \left[\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \end{matrix}\right]. \end{equation}
Is this a symmetry of the ZnO crystal?
(c) Sketch the phonon dispersion relation of ZnO. The distances to the Brillouin zone boundaries are,
\begin{equation} \overline{\Gamma A}=\frac{\pi}{c},\,\overline{\Gamma K}=\frac{4\pi}{3a},\,\overline{\Gamma M}=\frac{2\pi}{\sqrt{3}a},\,\overline{MK}=\frac{2\pi}{3a}. \end{equation}(d) The integral of the phonon density of states over all frequencies is the total number of phonon modes. How many phonon modes are there in a cubic meter of ZnO?
(e) ZnO is transparent to visible light. What can you conclude from this about the electronic band structure? Sketch the electronic dispersion relation of ZnO.
Problem 3
(a) Aluminum has a molar mass of 26.98 g/mol and a mass density of ρ = 2.70 g/cm³. Calculate the electron density under the assumption that each atom contributes 3 valence electrons to the free electrons.
(b)What experiments could you perform that could be used to determine the electron density? List as many experiments as you can think of.
(c) A metal with a simple cubic Bravais lattice has one valence electron per unit cell. How large is the Fermi wave vector $k_F$ compared to $|\vec{k}|$ at the symmetry point $\text{R}$ at the corner of the Brillouin zone?
Problem 4
The concentration of electrons in the conduction band is $n = N_c\exp\left(\frac{\mu-E_c}{k_BT}\right)$ and holes in the valence band is $p = N_v\exp\left(\frac{E_v-\mu}{k_BT}\right)$. Below are some parameters of semiconductors.
$N_c$ | $N_v$ | $E_g$ | |
Si (300 K) | 2.78 × 1025 m-3 | 9.84 × 1024 m-3 | 1.12 eV |
Ge (300 K) | 1.04 × 1025 m-3 | 6.0 × 1024 m-3 | 0.66 eV |
GaAs (300 K) | 4.45 × 1023 m-3 | 7.72 × 1024 m-3 | 1.424 eV |
4H-SiC (300 K) | 1.7 × 1025 m-3 | 2.5 × 1025 m-3 | 3.3 eV |
(a) What is the chemical potential for intrinsic Ge measured from the top of the valence band at 300 K?
(b) Draw the electron density of states for Ge as a function of energy near the top of the valence band and the bottom of the conduction band. Does the density of states rise more steeply at the valence band or the conduction band?
(c) In silicon, the mobility of electrons is 1500 cm²/Vs and the mobility of holes is 450 cm²/Vs. What is the conductivity of intrinsic silicon at 400 °C?
Quantity | Symbol | Value | Units | |
| electron charge | e | 1.60217733 × 10-19 | C | |
| speed of light | c | 2.99792458 × 108 | m/s | |
| Planck's constant | h | 6.6260755 × 10-34 | J s | |
| reduced Planck's constant | $\hbar$ | 1.05457266 × 10-34 | J s | |
| Boltzmann's constant | kB | 1.380658 × 10-23 | J/K | |
| electron mass | me | 9.1093897 × 10-31 | kg | |
| Stefan-Boltzmann constant | σ | 5.67051 × 10-8 | W m-2 K-4 | |
| Bohr radius | a0 | 0.529177249 × 10-10 | m | |
| atomic mass constant | mu | 1.6605402 × 10-27 | kg | |
| permeability of vacuum | μ0 | 4π × 10-7 | N A-2 | |
| permittivity of vacuum | ε0 | 8.854187817 × 10-12 | F m-1 | |
| Avogado's constant | NA | 6.0221367 × 1023 | mol-1 |