Linear Chain

Einstein Model

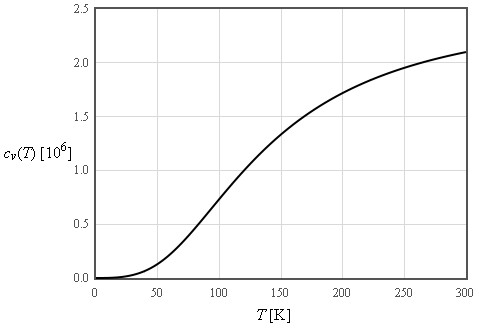
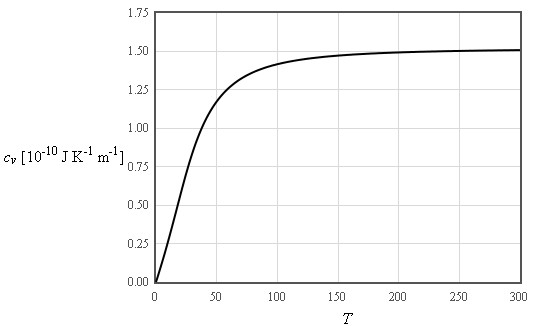
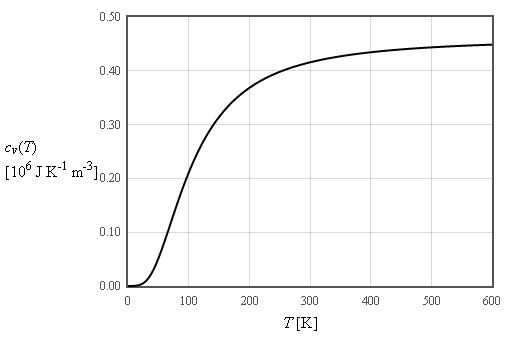
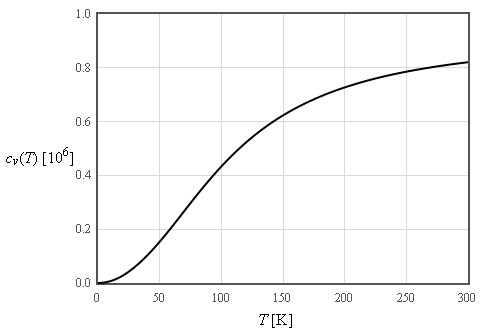
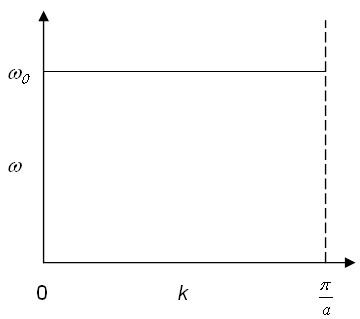
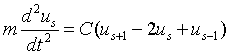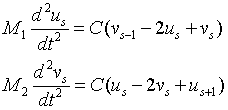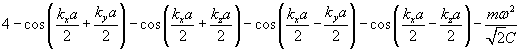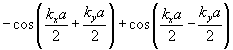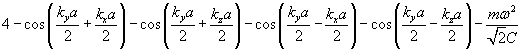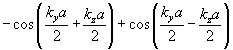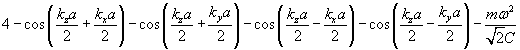Einstein assumed that all of the 3N normal modes of a crystal containing N atoms have the same frequency ω₀. This is not a good model for the dispersion relation but it does a reasonable job in describing the specific heat.

Debye Model

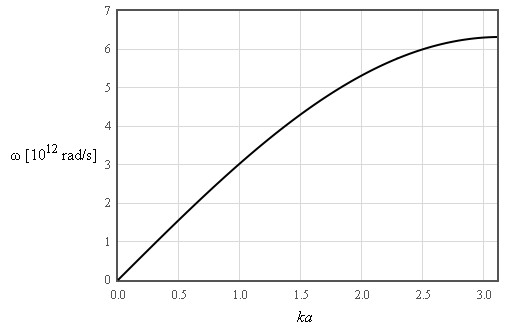
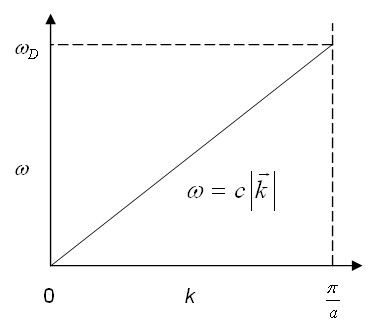
Debye used the long wavelength limit where the density of states increases like ω² up to a cut-off frequency where the density of states is assumed to abruptly go to zero. The cut-off is chosen so that the total number of states is 3N.

Linear chain 2 masses

simple cubic

body centered cubic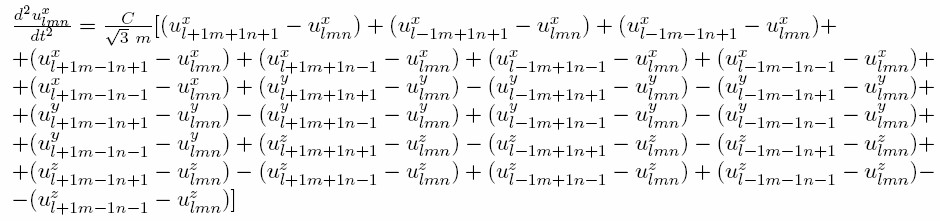

And similar expressions for the y and z directions

face centered cubic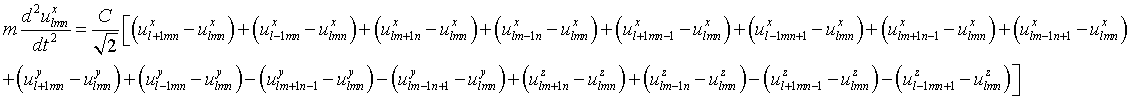

And similar expressions for the y and z directions

hexagonal close pack pdf Mathematica notebook

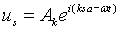
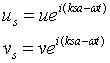
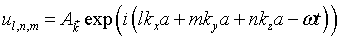
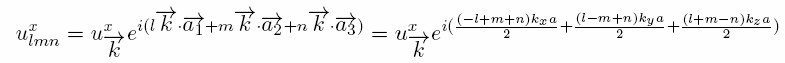
And similar expressions for the y and z directions

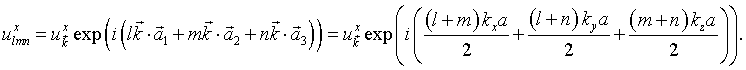
And similar expressions for the y and z directions

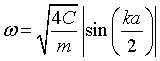
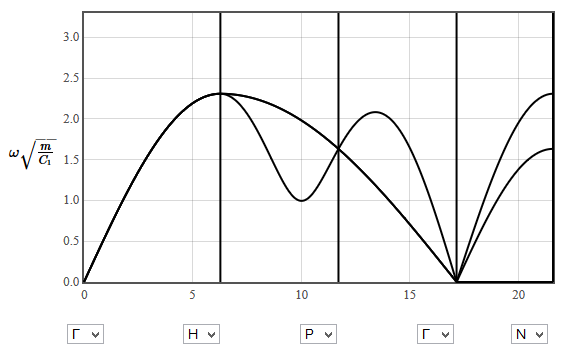
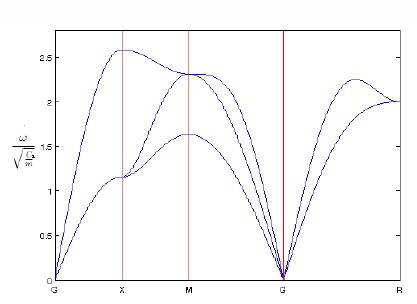
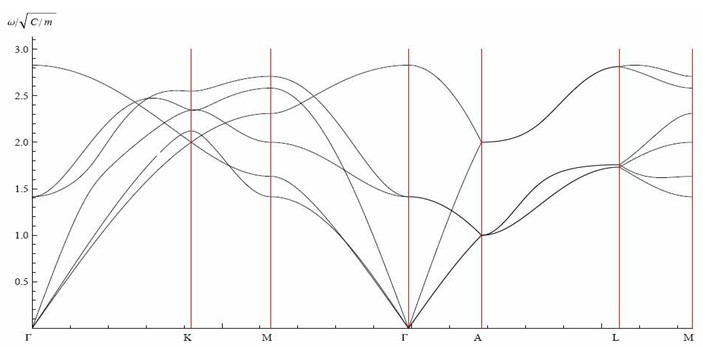
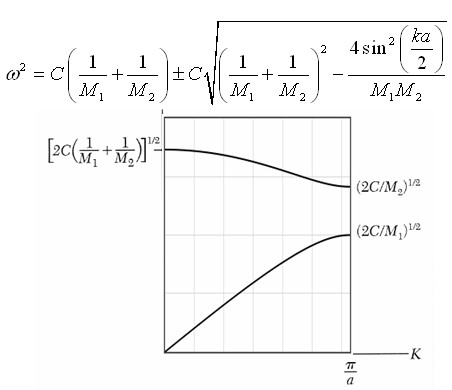
The dispersion relation can be expressed as the following determinant

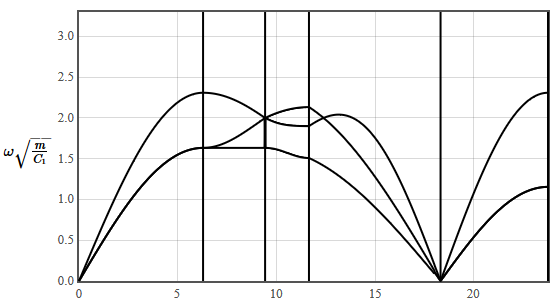
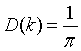
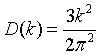
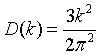
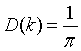
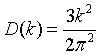
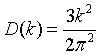
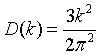
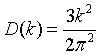
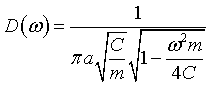
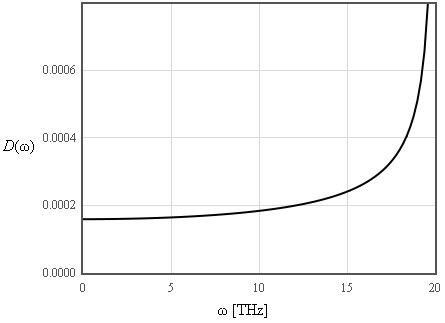
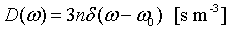
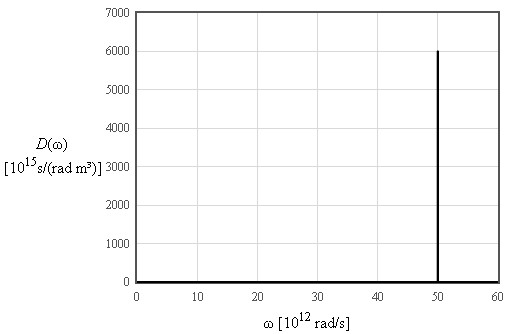
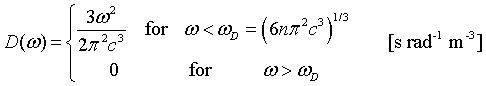
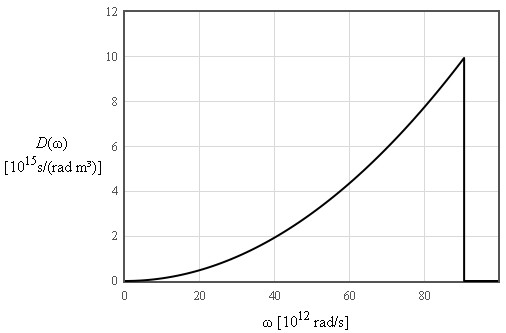
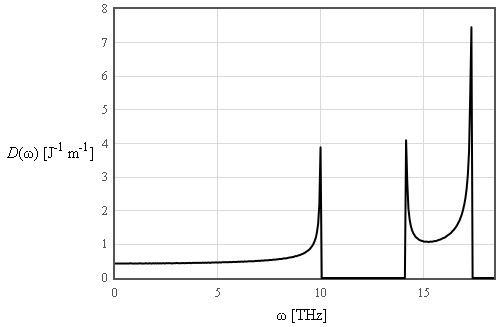
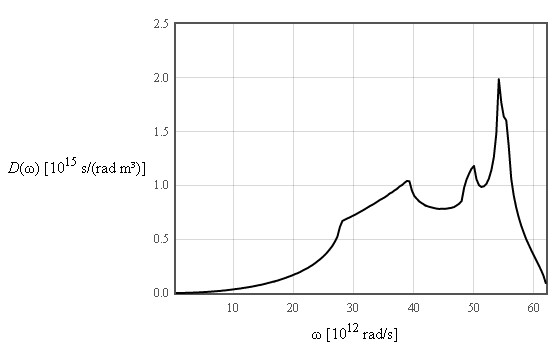
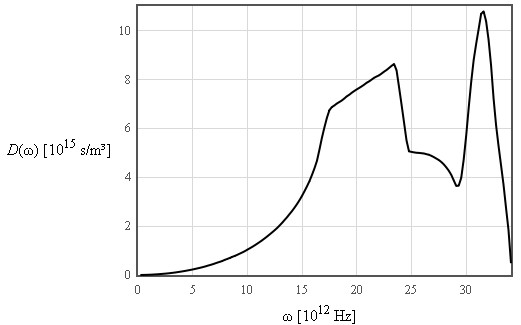
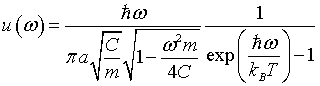
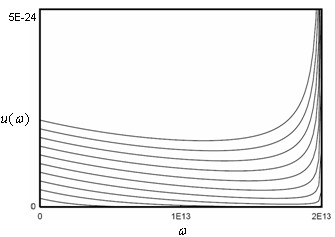
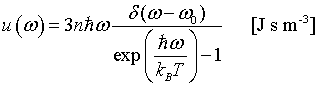
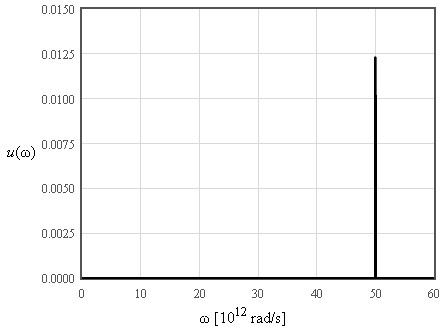
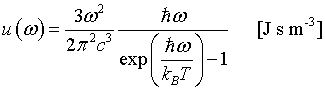
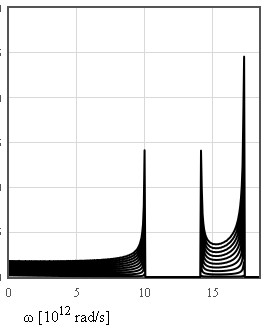
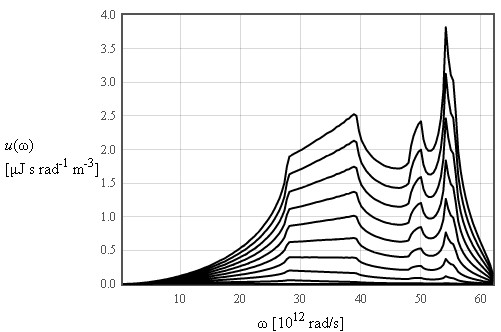
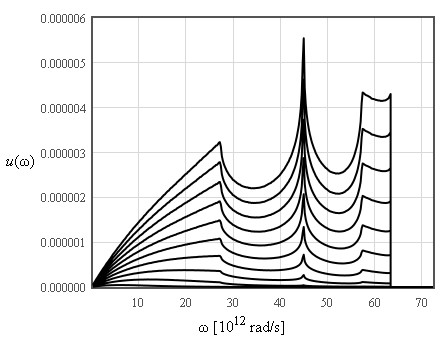
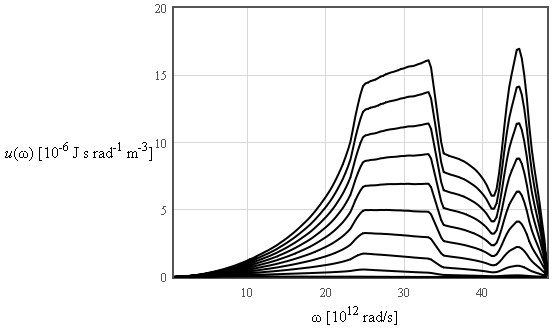
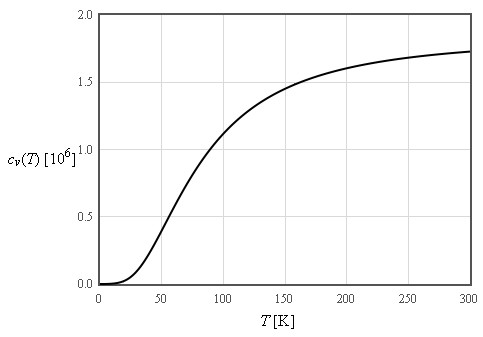
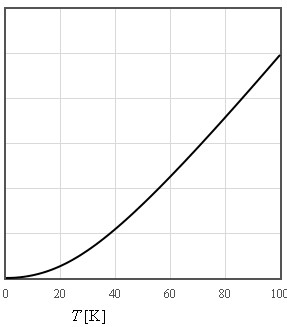
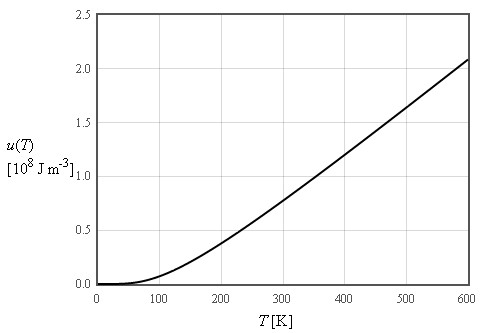
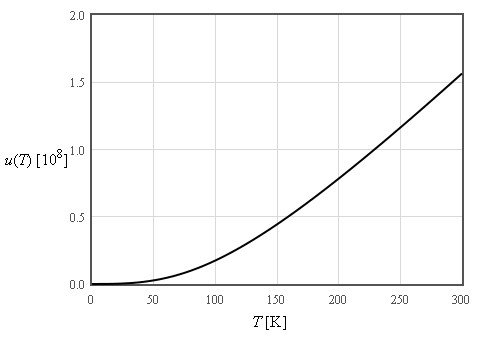
The internal energy increases like T² at low temperatures and is linear in T at high temperatures

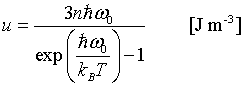
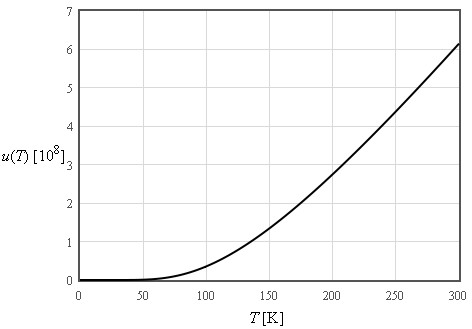
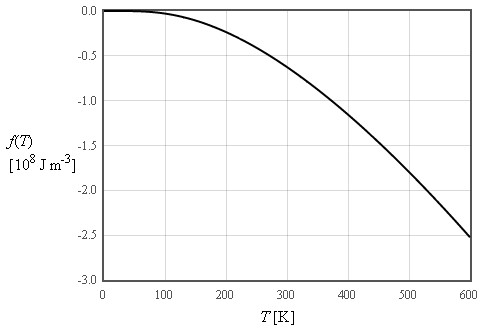
$\large u\approx \frac{3\pi^4}{5}nk_B\frac{T^4}{\Theta_D^3}\quad\left[\text{J/m}^3\right]$
$\large \text{For}\quad T << \Theta_D$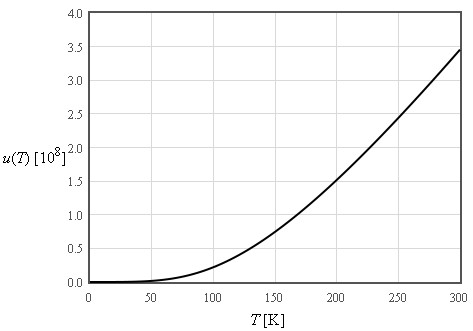

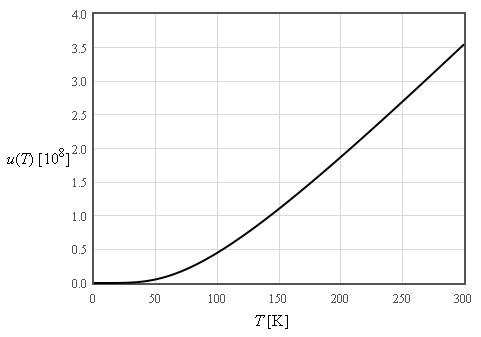
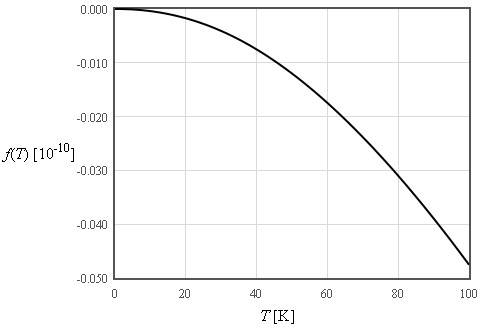
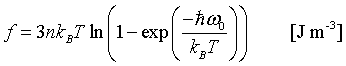
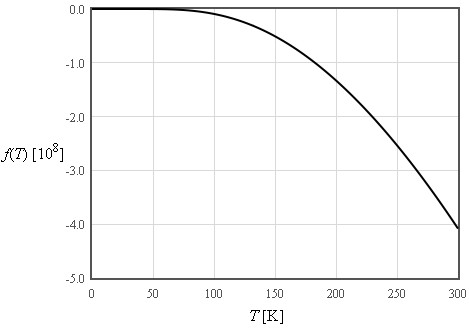
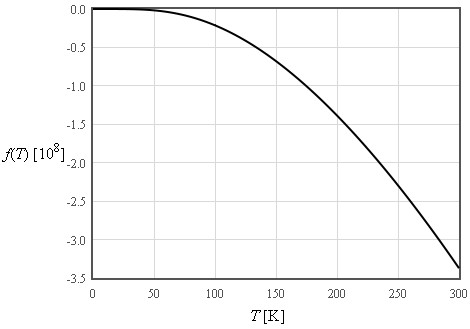
$\large f\approx -\frac{\pi^4}{5}nk_B\frac{T^4}{\Theta_D^3}\quad\left[\text{J/m}^3\right]$
$\large \text{For}\quad T << \Theta_D$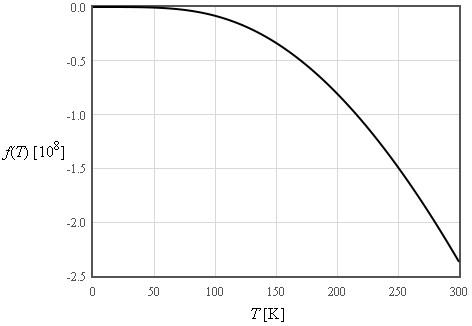

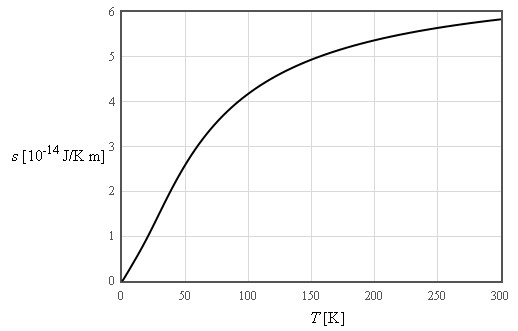
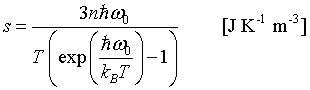
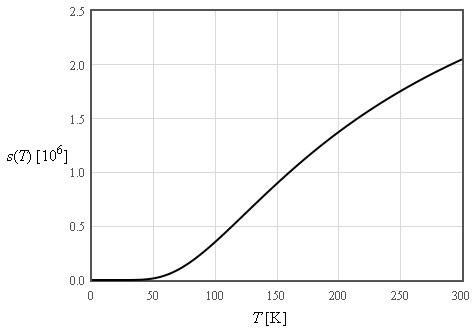
$\large s\approx \frac{4\pi^4}{5}nk_B\left(\frac{T}{\Theta_D}\right)^3\quad\left[\text{J K}^{-1}\text{m}^{-3}\right]$
$\large \text{For}\quad T << \Theta_D$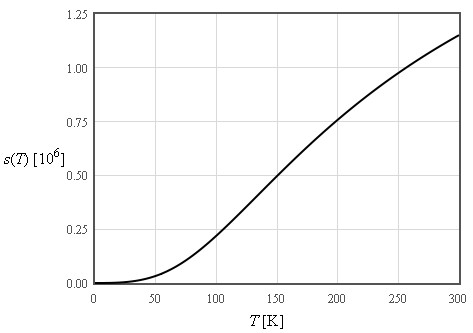

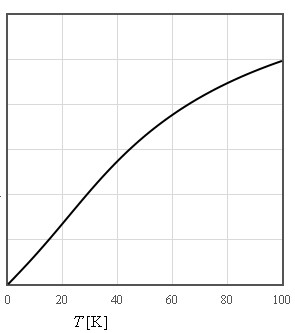
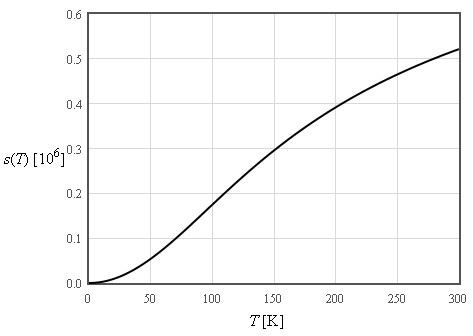
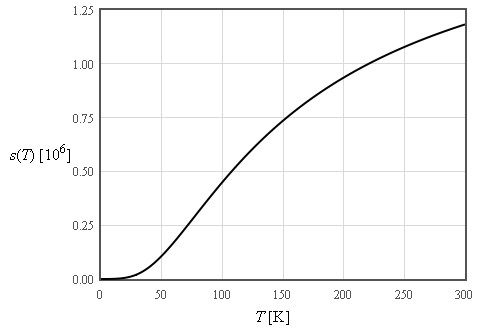
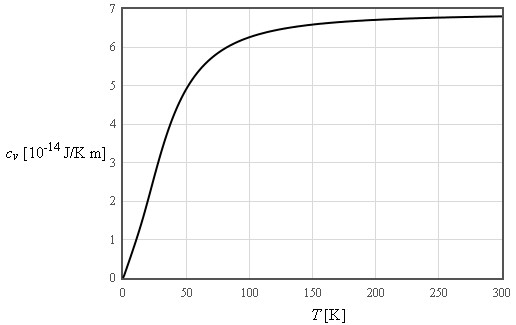
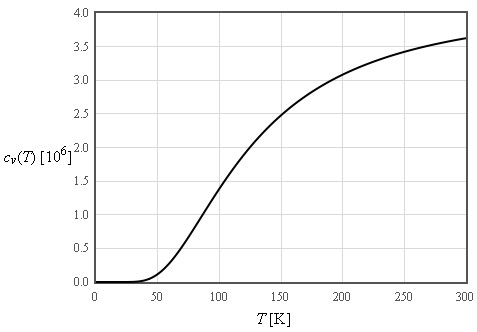
$\large c_v\approx \frac{12\pi^4}{5}nk_B\left(\frac{T}{\Theta_D}\right)^3\quad\left[\text{J K}^{-1}\text{m}^{-3}\right]$
$\large \text{For}\quad T << \Theta_D$