PHY.K02UF Molecular and Solid State Physics
|
| ||||
PHY.K02UF Molecular and Solid State Physics | ||||
The phonon dispersion relation for fcc can be calculated by modelling the crystal as a lattice of equal masses connected by linear springs. The primitive lattice vectors of an fcc crystal are,
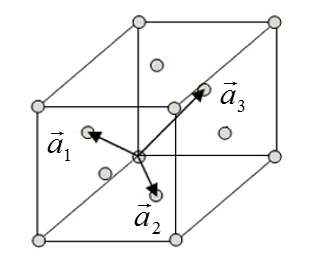 | $$\vec{a}_1=\frac{a}{2}(\hat{x}+\hat{z}),$$ $$\vec{a}_2=\frac{a}{2}(\hat{x}+\hat{y}),$$ $$\vec{a}_3=\frac{a}{2}(\hat{y}+\hat{z}).$$ |
Consider an fcc crystal with one atom in the basis. Let $u^x_{lmn}$ the displacement the atom in the unit cell at position $\vec{r}=l\vec{a}_1+m\vec{a}_2+n\vec{a}_3$ in the $x$-direction from its equilibrium position. If the restoring force that pushes the atoms back to their equilibrium positions is modelled with a linear spring with spring constants $C$, the equations of motion in this case are,
\begin{equation} \begin{split} M \frac {d^{2}u^{x}_{lmn}}{dt^{2}} & = \frac{C}{2}\Big[ (u^{x}_{(l+1)mn} - u^{x}_{lmn})+ (u^{x}_{(l-1)mn} - u^{x}_{lmn})+ (u^{x}_{l(m+1)n} - u^{x}_{lmn}) + (u^{x}_{l(m-1)n} - u^{x}_{lmn})\\ & + (u^{x}_{(l+1)m(n-1)} - u^{x}_{lmn})+ (u^{x}_{(l-1)m(n+1)} - u^{x}_{lmn})+ (u^{x}_{l(m+1)(n-1)} - u^{x}_{lmn})+ (u^{x}_{l(m-1)(n+1)}- u^{x}_{lmn})\\ & + (u^{y}_{l(m+1)n} - u^{y}_{lmn}) + (u^{y}_{l(m-1)n} - u^{y}_{lmn}) - (u^{y}_{(l+1)m(n-1)} - u^{y}_{lmn}) - (u^{y}_{(l-1)m(n+1)} - u^{y}_{lmn})\\ &+ (u^{z}_{(l+1)mn}- u^{z}_{lmn})+ (u^{z}_{(l-1)mn} - u^{z}_{lmn})-(u^{z}_{l(m+1)(n-1)} - u^{z}_{lmn})- (u^{z}_{l(m-1)(n+1)} - u^{z}_{lmn})\Big], \end{split} \end{equation} \begin{equation} \begin{split} M \frac {d^{2}u^{y}_{lmn}}{dt^{2}} &= \frac{C}{2}\Big[ (u^{y}_{l(m+1)n} - u^{y}_{lmn}) + (u^{y}_{l(m-1)n} - u^{y}_{lmn}) + (u^{y}_{(l+1)m(n-1)} - u^{y}_{lmn})+ (u^{y}_{(l-1)m(n+1)} - u^{y}_{lmn}) \\ &+ (u^{y}_{(l-1)(m+1)n} - u^{y}_{lmn}) + (u^{y}_{lm(n-1)} - u^{y}_{lmn}) + (u^{y}_{(l+1)(m-1)n} - u^{y}_{lmn}) + (u^{y}_{lm(n+1)} - u^{y}_{lmn})\\ &+ (u^{x}_{l(m+1)n} - u^{x}_{lmn}) + (u^{x}_{l(m-1)n} - u^{x}_{lmn}) - (u^{x}_{(l-1)m(n+1)} - u^{x}_{lmn}) - (u^{x}_{(l+1)m(n-1)} - u^{x}_{lmn}) \\ &+ (u^{z}_{lm(n-1)} - u^{z}_{lmn})+(u^{z}_{lm(n+1)} - u^{z}_{lmn}) - (u^{z}_{(l+1)(m-1)n} - u^{z}_{lmn})- (u^{z}_{(l-1)(m+1)n} - u^{z}_{lmn}) \Big], \end{split} \end{equation} \begin{equation} \begin{split} M \frac {d^{2}u^{z}_{lmn}}{dt^{2}} &= \frac{C}{2}\Big[ (u^{z}_{(l-1)mn} - u^{z}_{lmn})+ (u^{z}_{(l-1)l(m+1)n} - u^{z}_{lmn})+ (u^{z}_{l(m+1)(n-1)} - u^{z}_{lmn}) + (u^{z}_{lm(n-1)} - u^{z}_{lmn}) \\ &+ (u^{z}_{lm(n+1)} - u^{z}_{lmn})+ (u^{z}_{(l+1)mn} - u^{z}_{lmn})+ (u^{z}_{(l+1)(m-1)n} - u^{z}_{lmn})+ (u^{z}_{l(m-1)(n+1)} - u^{z}_{lmn})\\ &+ (u^{x}_{(l+1)mn} - u^{x}_{lmn}) + (u^{x}_{(l-1)mn} - u^{x}_{lmn})-(u^{x}_{l(m-1)(n+1)} - u^{x}_{lmn}) - (u^{x}_{l(m+1)(n-1)} - u^{x}_{lmn})\\ &+(u^{y}_{lm(n+1)} - u^{y}_{lmn}) + (u^{y}_{lm(n-1)} - u^{y}_{lmn}) - (u^{y}_{(l-1)(m+1)n} - u^{y}_{lmn})- (u^{y}_{(l+1)(m-1)n} - u^{y}_{lmn})\Big]. \end{split} \end{equation}The general solution of the normal modes of this crystal is required by symmetry to be,
$$\vec{u}_{lmn} = \vec{u}_{\vec{k}}\exp\left(i\left(l\vec{k}\cdot\vec{a}_1+m\vec{k}\cdot\vec{a}_2+n\vec{k}\cdot\vec{a}_3-\omega t\right)\right)=\vec{u}_{\vec{k}}\exp\left(i\frac{l+m}{2}k_xa\right)\exp\left(i\frac{m+n}{2}k_ya\right)\exp\left(i\frac{l+n}{2}k_za\right).$$Substituting this solution into the differential equations above results in the following algebraic equations,
\begin{equation} \begin{split} -\omega^2M u^{x}_{\vec{k}} & = \frac{C}{2}\Big[ e^{i(k_xa/2+k_za/2)} + e^{-i(k_xa/2+k_za/2)} + e^{i(k_xa/2-k_ya/2)} + e^{-i(k_xa/2-k_ya/2)} + e^{i(k_xa/2+k_ya/2)} + e^{-i(k_xa/2+k_ya/2)} + e^{i(k_xa/2-k_za/2)} + e^{-i(k_xa/2-k_za/2)} - 8 \Big] u^{x}_{\vec{k}}\\ & + \frac{C}{2}\Big[ e^{i(k_xa/2+k_ya/2)} + e^{-i(k_xa/2+k_ya/2)} - e^{i(k_xa/2-k_ya/2)} - e^{-i(k_xa/2-k_ya/2)} \Big] u^{y}_{\vec{k}}\\ &+ \frac{C}{2}\Big[ e^{i(k_xa/2+k_za/2)} + e^{-i(k_xa/2+k_za/2)} - e^{i(k_xa/2-k_za/2)} - e^{-i(k_xa/2-k_za/2)}\Big] u^{z}_{\vec{k}}, \end{split} \end{equation} \begin{equation} \begin{split} -\omega^2M u^{y}_{\vec{k}} &= \frac{C}{2}\Big[ e^{i(k_xa/2+k_ya/2)} + e^{-i(k_xa/2+k_ya/2)} - e^{i(k_xa/2-k_ya/2)} - e^{-i(k_xa/2-k_ya/2)} \Big] u^{x}_{\vec{k}}\\ &+ \frac{C}{2}\Big[e^{i(k_xa/2+k_ya/2)} + e^{-i(k_xa/2+k_ya/2)} + e^{i(k_xa/2-k_ya/2)} + e^{-i(k_xa/2-k_ya/2)} + e^{i(k_ya/2+k_za/2)} + e^{-i(k_ya/2+k_za/2)} + e^{i(k_ya/2-k_za/2)} + e^{-i(k_ya/2-k_za/2)} - 8 \Big] u^{y}_{\vec{k}}\\ &+ \frac{C}{2}\Big[ e^{i(k_ya/2+k_za/2)} + e^{-i(k_ya/2+k_za/2)} - e^{i(k_ya/2-k_za/2)} - e^{-i(k_ya/2-k_za/2)}\Big] u^{z}_{\vec{k}}, \end{split} \end{equation} \begin{equation} \begin{split} -\omega^2M u^{z}_{\vec{k}} & = \frac{C}{2}\Big[ e^{i(k_xa/2+k_za/2)} + e^{-i(k_xa/2+k_za/2)} - e^{i(k_xa/2-k_za/2)} - e^{-i(k_xa/2-k_za/2)}\Big] u^{x}_{\vec{k}}\\ & + \frac{C}{2}\Big[ e^{i(k_ya/2+k_za/2)} + e^{-i(k_ya/2+k_za/2)} - e^{i(k_ya/2-k_za/2)} - e^{-i(k_ya/2-k_za/2)} \Big] u^{y}_{\vec{k}}\\ & + \frac{C}{2}\Big[ e^{i(k_xa/2+k_za/2)} + e^{-i(k_xa/2+k_za/2)} + e^{i(k_ya/2-k_za/2)} + e^{-i(k_ya/2-k_za/2)} + e^{i(k_ya/2+k_za/2)} + e^{-i(k_ya/2+k_za/2)} + e^{i(k_xa/2-k_za/2)} + e^{-i(k_xa/2-k_za/2)} - 8 \Big] u^{z}_{\vec{k}}\\ \end{split} \end{equation}Using the identity $e^{i\theta}+e^{-i\theta}=2\cos(\theta)$, these equations can be written as an eigenvalue problem,
\begin{equation} \left[ \begin{array}{c} 4 - \cos\left(\frac{k_xa}{2} + \frac{k_ya}{2}\right) - \cos\left(\frac{k_xa}{2} + \frac{k_za}{2}\right) - \cos\left(\frac{k_xa}{2} - \frac{k_ya}{2}\right) - \cos\left(\frac{k_xa}{2} - \frac{k_za}{2}\right) & - \cos\left(\frac{k_xa}{2} + \frac{k_ya}{2}\right) + \cos\left(\frac{k_xa}{2} - \frac{k_ya}{2}\right) & - \cos\left(\frac{k_xa}{2} + \frac{k_za}{2}\right) + \cos\left(\frac{k_xa}{2} - \frac{k_za}{2}\right) \\ - \cos\left(\frac{k_xa}{2} + \frac{k_ya}{2}\right) + \cos\left(\frac{k_xa}{2} - \frac{k_ya}{2}\right) & 4 - \cos\left(\frac{k_xa}{2} + \frac{k_ya}{2}\right) - \cos\left(\frac{k_ya}{2} + \frac{k_za}{2}\right) - \cos\left(\frac{k_xa}{2} - \frac{k_ya}{2}\right) - \cos\left(\frac{k_ya}{2} - \frac{k_za}{2}\right) & - \cos\left(\frac{k_ya}{2} + \frac{k_za}{2}\right) + \cos\left(\frac{k_ya}{2} - \frac{k_za}{2}\right) \\ - \cos\left(\frac{k_xa}{2} + \frac{k_za}{2}\right) + \cos\left(\frac{k_xa}{2} - \frac{k_za}{2}\right) & - \cos\left(\frac{k_ya}{2} + \frac{k_za}{2}\right) + \cos\left(\frac{k_ya}{2} - \frac{k_za}{2}\right) & 4 - \cos\left(\frac{k_xa}{2} + \frac{k_za}{2}\right) - \cos\left(\frac{k_ya}{2} + \frac{k_za}{2}\right) - \cos\left(\frac{k_xa}{2} - \frac{k_za}{2}\right) - \cos\left(\frac{k_ya}{2} - \frac{k_za}{2}\right) \end{array} \right] \left[ \begin{array}{b} u_{\vec{k}}^x \\ u_{\vec{k}}^y \\ u_{\vec{k}}^z \end{array} \right]=\frac{M\omega^2}{C} \left[ \begin{array}{b} u_{\vec{k}}^x \\ u_{\vec{k}}^y \\ u_{\vec{k}}^z \end{array} \right] \end{equation}The solutions to these equations can be found by setting the determinant of the matrix equal to zero.