PHY.K02UF Molecular and Solid State Physics
|
| ||||
PHY.K02UF Molecular and Solid State Physics | ||||
The simplest neutral molecule is molecular hydrogen, H2, which consists of two electrons and two protons. The molecular orbital Hamiltonian in this case is the same as it is for the molecular hydrogen ion and the molecular orbitals are the same as for the molecular ion.
\[ \begin{equation} H_{\text{mo}}^{H_2}= - \frac{\hbar^2}{2m_e}\nabla^2 - \frac{e^2}{4\pi\epsilon_0 |\vec{r}-\vec{r}_A|}- \frac{e^2}{4\pi\epsilon_0 |\vec{r}-\vec{r}_B|} , \end{equation} \]where $\vec{r}_A$ and $\vec{r}_B$ are the positions of the two protons. Consider a linear combination of the two 1s orbitals, $\psi_{\text{mo}}=c_1\phi_{\text{1s}}(\vec{r}-\vec{r}_A) +c_2\phi_{\text{1s}}(\vec{r}-\vec{r}_B)$. The time independent Schrödinger equation is,
\begin{equation} H_{\text{mo}}\psi_{\text{mo}}=E\psi_{\text{mo}} . \end{equation}Multiply the Schrödinger equation from the left by each of the atomic orbitals and integrate over all space. This results in a set of 2 algebraic equations called the Roothaan equations.
\[ \begin{equation} \begin{matrix} \langle \phi_{\text{1s}}(\vec{r}-\vec{r}_A) | H_{\text{mo}} |\psi_{\text{mo}}\rangle =E\langle\phi_{\text{1s}}(\vec{r}-\vec{r}_A)|\psi_{\text{mo}} \rangle \\ \langle \phi_{\text{1s}}(\vec{r}-\vec{r}_B) | H_{\text{mo}} |\psi_{\text{mo}}\rangle =E\langle\phi_{\text{1s}}(\vec{r}-\vec{r}_B)|\psi_{\text{mo}} \rangle\\ \end{matrix} \end{equation} \]By substituting in the form for $\psi_{\text{mo}}$ from above, the Roothaan equations can be written in matrix form,
\[ \begin{equation} \left[ \begin{matrix} H_{11} & H_{12} \\ H_{12} & H_{11} \end{matrix} \right] \left[ \begin{matrix} c_1 \\ c_2 \end{matrix} \right] = E \left[ \begin{matrix} S_{11} & S_{12} \\ S_{12} & S_{11} \end{matrix} \right]\left[ \begin{matrix} c_1 \\ c_2 \end{matrix} \right], \end{equation} \]where
\[ \begin{equation} \begin{matrix} H_{11}=\langle \phi_{\text{1s}}(\vec{r}-\vec{r}_A)|H_{\text{mo}}^{H_2}|\phi_{\text{1s}}(\vec{r}-\vec{r}_A)\rangle, \\ H_{12}=\langle \phi_{\text{1s}}(\vec{r}-\vec{r}_A)|H_{\text{mo}}^{H_2}|\phi_{\text{1s}}(\vec{r}-\vec{r}_B)\rangle, \\ S_{11}=\langle \phi_{\text{1s}}(\vec{r}-\vec{r}_A)|\phi_{\text{1s}}(\vec{r}-\vec{r}_A)\rangle=1, \\ S_{12}=\langle \phi_{\text{1s}}(\vec{r}-\vec{r}_A)|\phi_{\text{1s}}(\vec{r}-\vec{r}_B)\rangle. \end{matrix} \end{equation} \]From experience with $2\times 2$ matrices of this form, we know that the eigenvectors of both the Hamiltonian matrix and the overlap matrix are,
\[ \begin{equation} \left[ \begin{matrix} c_1 \\ c_2 \end{matrix} \right] = \left[ \begin{matrix} 1 \\ 1 \end{matrix} \right],\left[ \begin{matrix} 1 \\ -1 \end{matrix} \right] \end{equation} \]It is easy to check that these are the correct eigenvectors but letting $\textbf{H}$ and $\textbf{S}$ operate on them. The energies are,
\[ \begin{equation} E_{+}= \frac{H_{11}+ H_{12}}{1+ S_{12}}, \qquad E_{-}= \frac{H_{11}- H_{12}}{1- S_{12}}. \end{equation} \]The normalized molecular orbitals are,
\[ \begin{equation} \psi_{\pm}= \frac{1}{\sqrt{2}}\left(\phi_{\text{1s}}(\vec{r}-\vec{r}_A) \pm \phi_{\text{1s}}(\vec{r}-\vec{r}_B)\right) \end{equation} \]The calculation of the matrix elements $H_{11}$, $H_{12}$, $S_{11}$, and $S_{12}$, is discussed on the page for the molecular hydrogen ion. The calculations are identical in this case. Both $H_{11}$ and $H_{12}$ are negative so the bonding orbital $\psi_+$, has a lower energy than the antibonding orbital $\psi_-$. The difference in the bond potentials for H2 and H2+ comes from how the ground state energy is evaluated. For H2+, there is only one electron so there are no electron-electron interactions. For H2, we must use a properly antisymmetrized two-electron wavefunction and include the electron-electron interactions. The two-electron ground state wavefunction for molecular hydrogen is,
\[ \begin{equation} \Psi(\vec{r}_1,\vec{r}_2)=\frac{1}{\sqrt{2}}\left|\begin{matrix} \psi_+\uparrow(\vec{r}_1) & \psi_+\downarrow(\vec{r}_1) \\ \psi_+\uparrow(\vec{r}_2) & \psi_+\downarrow(\vec{r}_2) \end{matrix}\right| = \frac{1}{2\sqrt{2}}\left(\phi_{\text{1s}}(\vec{r}_1-\vec{r}_A) + \phi_{\text{1s}}(\vec{r}_1-\vec{r}_B)\right)\left(\phi_{\text{1s}}(\vec{r}_2-\vec{r}_A) + \phi_{\text{1s}}(\vec{r}_2-\vec{r}_B)\right)(\uparrow\downarrow - \downarrow\uparrow). \end{equation} \]To calculate the bond potential, the energy of the two-electron wavefunction is evaluated with the electronic Hamiltonian that includes the electron-electron interactions and the proton-proton interactions.
\[ \begin{equation}\label{eq:helec} \begin{matrix} H_{\text{elec}}^{H_2}=- \frac{\hbar^2}{2m_e}\nabla^2_1 - \frac{\hbar^2}{2m_e}\nabla^2_2- \frac{e^2}{4\pi\epsilon_0 |\vec{r}_1-\vec{r}_A|}- \frac{e^2}{4\pi\epsilon_0 |\vec{r}_1-\vec{r}_B|}\\ - \frac{e^2}{4\pi\epsilon_0 |\vec{r}_2-\vec{r}_A|}- \frac{e^2}{4\pi\epsilon_0 |\vec{r}_2-\vec{r}_B|}+\frac{e^2}{4\pi\epsilon_0 |\vec{r}_1-\vec{r}_2|}+\frac{e^2}{4\pi\epsilon_0 |\vec{r}_A-\vec{r}_B|}. \end{matrix} \end{equation} \]For a given distance between the protons, $|\vec{r}_A-\vec{r}_B|$, the energy is evaluated by calculating,
\[ \begin{equation} E= \frac{\langle \Psi |H_{\text{elec}}^{H_2}|\Psi\rangle}{\langle \Psi|\Psi\rangle}. \end{equation} \]This is a six-dimensional integral because it is necessary to integrate over the $x$, $y$, and $z$ components of $\vec{r}_1$ and $\vec{r}_2$. The integral is difficult because of the singularities that occur when $\vec{r}_1=\vec{r}_A$, $\vec{r}_1=\vec{r}_B$, $\vec{r}_2=\vec{r}_A$, $\vec{r}_2=\vec{r}_B$, or $\vec{r}_1=\vec{r}_2$. The enegy is calculated as a function of the distance $|\vec{r}_A-\vec{r}_B|$ which results in a plot of the bond potential like the one below.
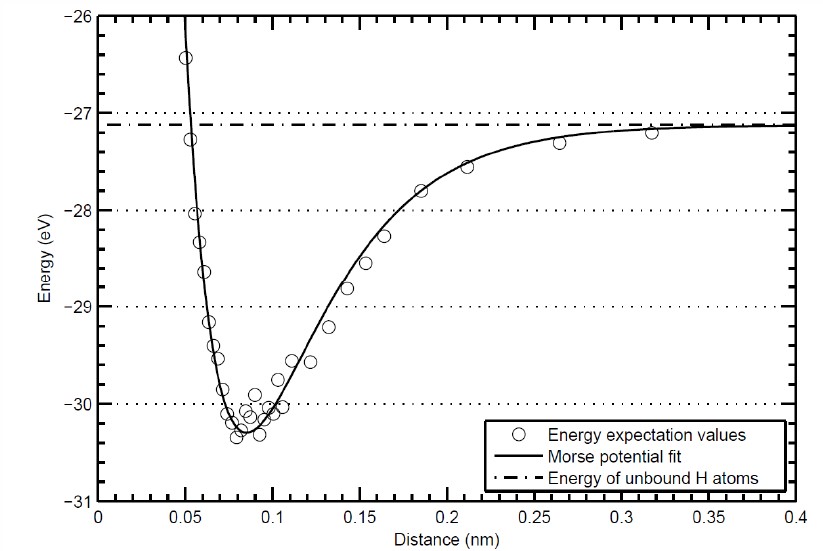
Electronic excitations
The first excited state of an H2 molecule has one electron in the bonding $\psi_+$ orbital and one in the antibonding $\psi_-$ orbital. This state will be split into a spin singlet and a spin triplet. There are four possible spin states: $\uparrow\uparrow$, $\downarrow\downarrow$, $\downarrow\uparrow$, $\uparrow\downarrow$. Four Slater determinants can be constructed for the four spin possibilities. These four two-electron wavefunctions span a certain function space. The functions with spin $\uparrow\uparrow$ and $\downarrow\downarrow$ have an antisymmetric orbital part of the wavefunction. Make a transformation of the wavefunctions with spin $\downarrow\uparrow$ and $\uparrow\downarrow$ to wavefunctions with spin $(\downarrow\uparrow +\uparrow\downarrow)/\sqrt{2}$ and $(\downarrow\uparrow -\uparrow\downarrow)/\sqrt{2}$. The wavefunction with spin $(\downarrow\uparrow +\uparrow\downarrow)/\sqrt{2}$ has an antisymmetric orbital part while the wavefunction with spin $(\downarrow\uparrow -\uparrow\downarrow)/\sqrt{2}$ has a symmetric orbital part. When the energies of these four wavefunctions are evaluated using the $H_{\text{elec}}^{H_2}$ Hamiltonian, the three wavefunctions with the antisymmetric orbital part will have the same energy; this is the spin triplet. The one wavefunction with the symmetric orbital part will have a different energy and is the spin singlet. If a magnetic field is applied, it will couple to the spin and split the spin triplet state into three energy levels.
Vibrational states
The quantum calculations of the bond potential yields a bond length of $r_0$ = 0.74 Å and a dissociation energy $U_0$ = 4.52 eV. These parameters can be used with the Morse potential to calculate the vibrational states of the H2 molecule. Since there are two atoms in this molecule there are six degrees of freedom corresponding to the $x$, $y$, and $z$ motion of the two atoms. There are 3 translational degrees of freedom. Since is a linear molecule, there are two rotational degrees of freedom. This means there is just one vibration degree of freedom $(3N-5=1)$.
Rotational states
The rotational energy levels can be estimated using a rigid rotator model where the energies are given by,
where $I$ is the moment of inertia. The quantum calculations of the bond potential yields a bond length of $r_0$ = 0.74 Å. This can be used to calculate the moment of inertia,
\[ \begin{equation} I= 2m_H(r_0/2)^2 = 4.58\times 10^{-48}\hspace{0.2cm}\text{kg m}^2, \end{equation} \]where $m_H$ is the mass of a hydrogen atom. The energy between the $\mathcal{l}=0$ and $\mathcal{l}=1$ levels is, \[ \begin{equation} \Delta E= \frac{\hbar^2}{I}=2.4\times 10^{-21}\hspace{0.2cm}\text{J}\hspace{0.1cm}=\hspace{0.1cm}15\hspace{0.2cm}\text{meV}. \end{equation} \]
This agrees with the value calculated from the spectroscopic constants.