PHY.K02UF Molecular and Solid State Physics
|
| ||||
PHY.K02UF Molecular and Solid State Physics | ||||
The Van der Waals force is a weak, short-range force that arises from temporal fluctuations of the charge distribution. This force can attract ideal gas atoms together. Ideal gas atoms are electrically neutral so there is no Coulomb attraction between them. The average dipole moment of an ideal gas atom is zero but the charge fluctuates around its average position and can temporarily create a dipole moment. This dipole moment induces a response in the neighboring atom such that there is a net attractive force between the atoms. The average over the attractive forces caused by the charge fluctuations is the Van der Walls force.
 | 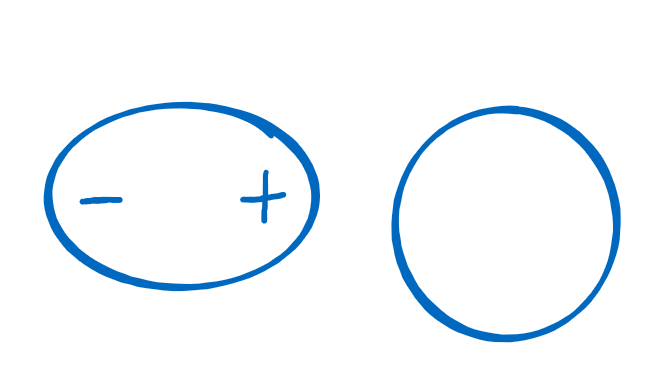 | 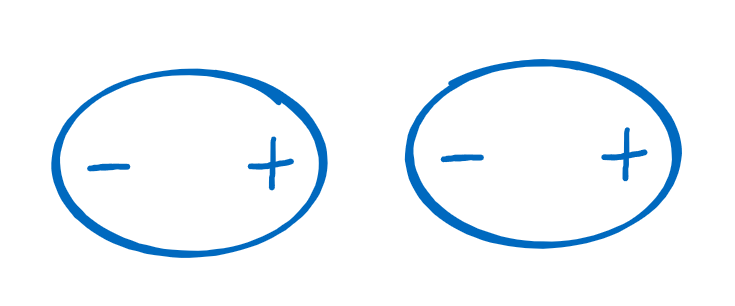 | ||
Two neutral atoms. | A charge fluctation | The dipole induces a |
The bonds between atoms held together by Van der Waals forces are weak with a bond energy of a few meV. The Van der Waal bond potential is often approximated by a Lennard-Jones potential of the form,
$$U(R)= 4\epsilon\left[\left(\frac{\sigma}{R}\right)^{12}-\left(\frac{\sigma}{R}\right)^{6}\right].$$In this equation $\epsilon$ corresponds to the depth of the potential, which is typically a small number.
Some quantum mechanically calculated bond potentials and fits to the Lennard-Jones form for some noble gas molecules are shown below.
| He2 | ||
|---|---|---|
| U(R) [eV] |
$\hspace{1cm}\sigma= 2.411$ Å $\hspace{1cm}\epsilon=4.570$ meV | |
R [Å] |
| Ar2 | ||
|---|---|---|
| U(R) [eV] |
$\hspace{1cm}\sigma= 3.425$ Å $\hspace{1cm}\epsilon=13.66$ meV | |
R [Å] |
| Kr2 | ||
|---|---|---|
| U(R) [eV] |
$\hspace{1cm}\sigma= 3.698$ Å $\hspace{1cm}\epsilon=18.2$ meV | |
R [Å] |
| Ne2 | ||
|---|---|---|
| U(R) [eV] |
$\hspace{1cm}\sigma= 2.687$ Å $\hspace{1cm}\epsilon=8.56$ meV | |
R [Å] |
The $\frac{1}{R^6}$ behavior of the Van der Waals interaction is calculated in more detail in the Advanced Quantum Mechanics course.