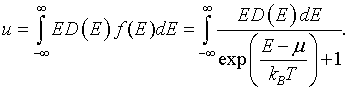
The internal energy density u is the integral of the energy E times the density of states D(E) times the probability that those states are occupied. The occupation probablility is given by the Fermi function f(E).
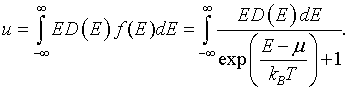
Here μ is the chemical potential which can be calculated from the density of states and the electron density. (Calculate μ)
The numerical calculation of the internal energy goes faster if we first integrate by parts,
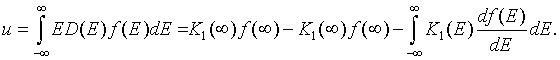
Here the function K1(E) is,

The boundary terms vanish because K1(-∞) = 0 and f(∞) = 0. The electron density can then be written as,
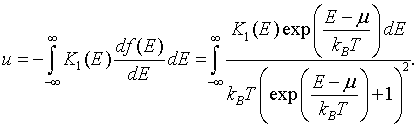
This is a convenient form since the derivative of the Fermi function df/dE is only significantly different from zero in the range from μ - 7kBT to μ + 7kBT.
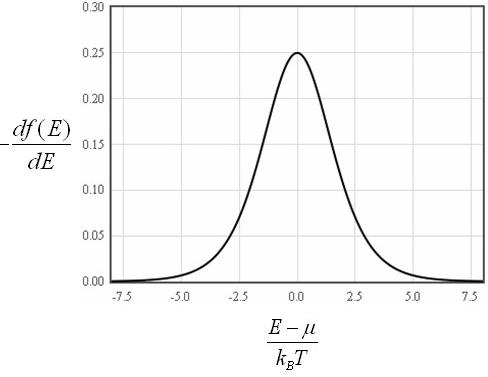
This means that the internal energy density can be approximated as,
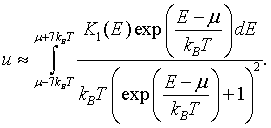
For metals, the integral of the density of states K1(E) is a monotonically increasing function of energy. If K1(E) is known at a set of discrete points, K1(E1), K1(E2),...K1(EN), then the electron density can be approximated as,
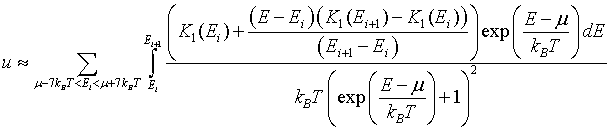
The integral can be performed to yield,
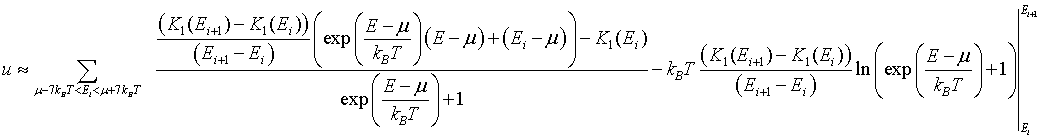
The form below calculates the internal energy density numerically from the density of states. The density of states is input as two columns of text in the textbox below. The first column is the energy in eV. The second column is the density of states in unit of eV-1 m-d, where d is the dimensionality (1,2, or 3). The electron density can be calculated from the number of electrons per unit cell and the volume of the unit cell or it can be input directly. After the 'DoS → u' button is pressed, the internal energy density is plotted at a function of temperature.
| D(E) [eV-1 m-5] | u [eV m-5] | |||
E [eV] | T [K] | |||
|
Free electron model:
Tight binding: