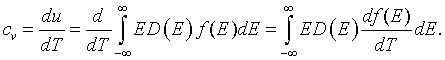
The specific heat cv is the derivative of the internal energy density with respect to temperature.
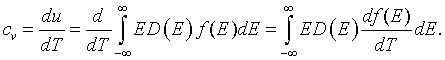
Here E is the energy, D(E) is the density of states, and f(E) is the Fermi function. The derivative of the Fermi function is,
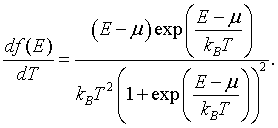
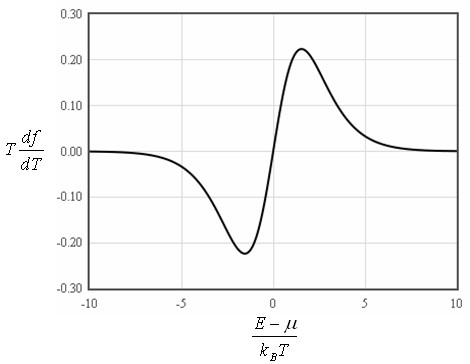
The derivative of the Fermi function df/dT is only significantly different from zero in the range from μ - 10kBT to μ + 10kBT.
The specific heat can be approximated as,
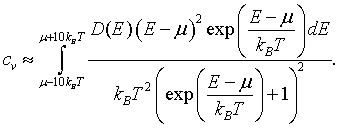
The form below calculates the internal energy density numerically from the density of states. The density of states is input as two columns of text in the textbox below. The first column is the energy in eV. The second column is the density of states in unit of eV-1 m-d, where d is the dimensionality (1,2, or 3). The electron density can be calculated from the number of electrons per unit cell and the volume of the unit cell or it can be input directly. After the 'DoS → cv' button is pressed, the specific heat is plotted as a function of temperature.
| D(E) [eV-1 m-] | cv [eV m- K-1] | |||
E [eV] | T [K] | |||
|
Free electron model:
Tight binding: