|
|
|
|
|
|
|
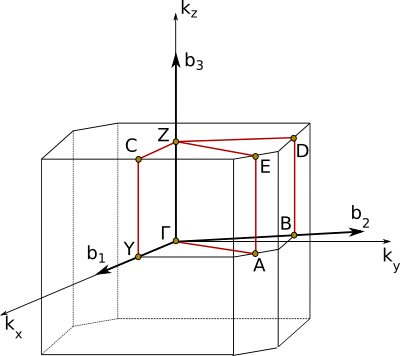
| Symmetry points |
| ($u,v,w$) | [$k_x,k_y,k_z$] |
| Γ: (0, 0, 0) |
[0, 0, 0] |
| Y: (0, 1/2, 0) |
[0, $\frac{\pi}{b \, \sin(\alpha)}$, 0] |
| B: (1/2, 0, 0) |
[$-\frac{\pi}{a}$, $-\frac{\pi}{a \, \tan(\alpha)}$, 0] |
| A: (1/2, 1/2, 0) |
[$-\frac{\pi}{a}$,
$-\frac{\pi}{a \, \tan(\alpha)}+\frac{\pi}{b \, \sin(\alpha)}$, 0] |
| Z: (0, 0, 1/2) |
[0, 0, $\frac{\pi}{c}$] |
| C: (0, 1/2, 1/2) |
[0, $\frac{\pi}{b \, \sin(\alpha)}$, $\frac{\pi}{c}$] |
| D: (1/2, 0, 1/2) |
[$-\frac{\pi}{a}$,
$-\frac{\pi}{a \, \tan(\alpha)}$, $\frac{\pi}{c}$] |
| E: (1/2, 1/2, 1/2) |
[$-\frac{\pi}{a}$,
$-\frac{\pi}{a \, \tan(\alpha)}+\frac{\pi}{b \, \sin(\alpha)}$, $\frac{\pi}{c}$] |
|
|
Please note:
The k-values are evaluated on the straight line connecting two succeeding symmetry points.
Intermediary corners - as they occur for instance on the path between Y and A - will be neglected.
Therefore, paths like Γ-Y-C-Z or Γ-A-E-Z should be preferred over paths like Y-A-B.
|
|
\[ \begin{equation}
\vec{b}_1=\frac{-2\pi}{a}(\hat{k}_x + \frac{1}{\tan(\alpha)}\hat{k}_y),
\hspace{1cm} \vec{b}_2=\frac{2\pi}{b\, \sin(\alpha)}\hat{k}_y,
\hspace{1cm} \vec{b}_3=\frac{2\pi}{c}\hat{k}_z.
\end{equation} \]
|
|
