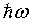 times the density of states D(ω) times the probability that the state is occupied. This probability is given by the Bose-Einstein factor.
times the density of states D(ω) times the probability that the state is occupied. This probability is given by the Bose-Einstein factor.For photons, the energy spectral density u(ω) is the energy of a boson 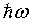 times the density of states D(ω) times the probability that the state is occupied. This probability is given by the Bose-Einstein factor.
times the density of states D(ω) times the probability that the state is occupied. This probability is given by the Bose-Einstein factor.
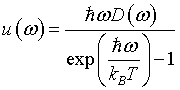
The form below can be used to calculate the energy spectral density from the density of states. The density of states is input as two columns of text in the lower left textbox. The first column is the angular frequency ω in rad/s. The second column is the density of states. The units of the density of states depend on the dimensionality. In one dimension the units are s/m, in two dimensions the units are s/m², and in three dimensions the units are s/m³. After the 'DoS → u(ω)' button is pressed, the density of states is plotted on the left and u(ω) is plotted on the right. The data for the u(ω) plot also appear as eleven columns of text in the lower right textbox. The first column is the angular frequency ω in rad/s. Columns 2-11 are the energy spectral density u(ω) for ten temperatures 0.1Tmax, 0.2Tmax...Tmax in units of J s rad-1 m-1, J s rad-1 m-2, or J s rad-1 m-3 depending on the dimensionality.
| D(ω) | u(ω) [10-15] | |||
ω [1015 rad/s] | ω [1015 rad/s] | |||
Density of states: | u(ω): | |||
Photons in vacuum: