PHY.K02UF Molecular and Solid State Physics
|
| ||||
PHY.K02UF Molecular and Solid State Physics | ||||
The complex exponentials such as those that are used for a Fourier series are often called plane waves. A plane wave has the form,
$$e^{i\vec{k}\cdot\vec{r}} = \cos \left(\vec{k}\cdot\vec{r}\right) + i\sin \left(\vec{k}\cdot\vec{r}\right).$$Here $\vec{k} = k_x\,\hat{x}+k_y\,\hat{y}+k_z\,\hat{z}$ is a vector called a wave vector. Consider the value of the plane wave at a particular point $\vec{r}$. In general, the value at this point is some complex number. Now move away from that point in a direction perpendicular to $\vec{k}$ to $\vec{r}+\vec{r}_{\perp}$. Every point on the plane that passes through $\vec{r}$ and is perpendicular to $\vec{k}$ has the same value, $e^{i\vec{k}\cdot\left(\vec{r} +\vec{r}_{\perp}\right)} = e^{i\vec{k}\cdot\vec{r}}$.
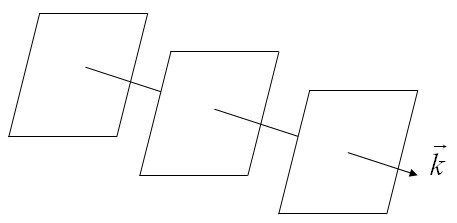
If you move in a direction parallel to $\vec{k}$, the function oscillates with a wavelength $\lambda = 2\pi/|\vec{k}|$. The real parts of some plane waves are plotted below. You just have to imagine the imaginary parts.
$\vec{k}=6\,\hat{x}$ | $\vec{k}=6\,\hat{y}$ | $\vec{k}=4\,\hat{x}+4\,\hat{y}$ | $\vec{k}=3\,\hat{x}-5\,\hat{y}$ |
Reciprocal space is a space of plane waves. Every point in a reciprcal space spanned by the vectors $\vec{k}=k_x\hat{k}_x+k_y\hat{k}_y+k_y\hat{k}_y$ corresponds to a plane wave. The direction of the $k$-vector indicates the direction the plane wave is moving and $2\pi/|\vec{k}|$ is the wavelength of the plane wave. A distance $|\vec{k}|$ measured in reciprocal space is measured in unit of 1/meters and this is why the space is reciprocal. A reciprocal lattice is a periodic arrangement of points in reciprocal space.

The red vector is a $k$-vector in reciprocal space. The black points represent a reciprocal lattice.
We have found that a discrete sum of plane waves can be used to describe a periodic function,
$$ f\left(\vec{r}\right)= \sum\limits_{\vec{G}} f_{\vec{G}}e^{i\vec{G}\cdot\vec{r}}.$$Here the reciprocal lattice points $\vec{G}$ are a lattice of points in reciprocal space. Now consider functions that can be expressed as a continuous sum of plane waves,
$$ f\left(\vec{r}\right)= \int F\left(\vec{k}\right)e^{i\vec{k}\cdot\vec{r}}d\vec{k} .$$The integral in this last expression extends over all values of $\vec{k}$ in reciprocal space. The function $F\left(\vec{k}\right)$ is a weighting function that tells us how much of plane wave $\vec{k}$ should be included in the sum. The quantity $F\left(\vec{k}\right)$ called the Fourier transform of $f\left(\vec{r}\right)$ and is a function in $k$-space. For physically relevant quantities, $F\left(\vec{k}\right)$ typically goes to zero for large values of $|\vec{k}|$ so that the integral is well defined.
All of the information needed to specify $f\left(\vec{r}\right)$ is contained in $F\left(\vec{k}\right)$. The converse is also true. The Fourier transform $F\left(\vec{k}\right)$ of $f\left(\vec{r}\right)$ can be calculated by,
$$ F\left(\vec{k}\right)= \frac{1}{\left( 2\pi \right)^d} \int f\left(\vec{r}\right)e^{-i\vec{k}\cdot\vec{r}}d\vec{r} .$$Here $d$ is the number of dimensions the function $f\left(\vec{r}\right)$ is defined in.