
Every periodic function is associated with a Bravais lattice. You can think of the function as being defined in a primitive unit cell and then repeating the primitive unit cell at every point of the Bravais lattice.
A periodic function can be written as a Fourier series in the form,

where G are the reciprocal lattice vectors of the Bravais lattice and fG are complex coefficients. If f(r) is a real function, then f-G = fG*.
Using the definition of a reciprocal lattice vector,

the Fourier series can be rewritten in terms of the primitive reciprocal lattice vectors, bi.

An example of a real periodic function that has an orthorhombic Bravais lattice can be constructed using the reciprocal lattice vectors 100, -100, 010, 0-10, 001, 00-1. If for all of these reciprocal lattice points fG = 1, then the periodic function is,

In a similar manner, periodic functions with a bcc, fcc, or hexagonal Bravais lattice can be constructed.
| bcc: |  |
| fcc: | 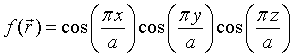 |
| hexagonal: | 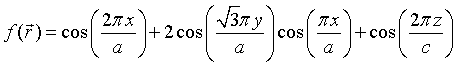 |
If the periodic function f(r) is known, the Fourier coefficients fG can be determined by multiplying both sides of Eq. [1] by exp(-iG'·r) and integrating over a primitive unit cell.
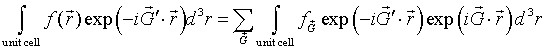
The left-hand side is the Fouier transform of the function f(r) restricted to a unit cell. On the right-hand side, only the term where G = G' contributes and the integral evaluates to fG times the volume V of the primitive unit cell.
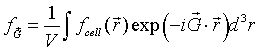
The function fcell(r) = f(r) within the primitive unit cell and is zero outside the primitive unit cell. The Fourier coefficient fG is the Fourier transform of the function fcell(r) divided by the volume.
Example 1: cubes repeated on a bcc lattice
Cubes are arranged on a bcc lattice such that the corners of the cubes just touch.

A three-dimensional periodic function f is defined such that it has a constant value C inside the cubes and is zero outside the cubes. This function can be expressed as a Fourier series,
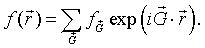
The Fourier coefficients fG are given by,
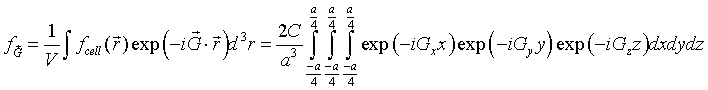
The cube at the origin lies entirely within the Wigner-Seitz cell and the function f is zero outside the cube so we just need to integrate over the cube. The integrals over x, y and z are easily performed.
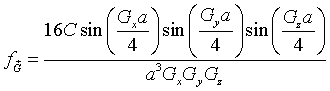
This result can readily be generalized to any rectangular cuboid with dimensions Lx×Ly×Lz that is repeated on any three-dimensional Bravais lattice. As long as a primitive unit cell can be defined such that the cuboid is entirely within the cell, the Fourier series for a function that has the value C inside the cuboids and zero outside the cuboids is,
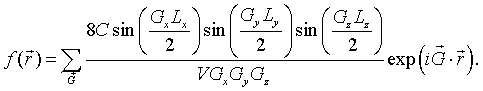
Here V is the volume of the primitive unit cell.
Example 2: spheres on an fcc lattice
Spheres of radius R are arranged on a fcc lattice.
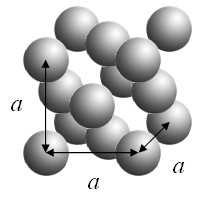
A three-dimensional periodic function f is defined such that it has a constant value C inside the spheres and is zero outside the spheres. This function can be expressed as a Fourier series,
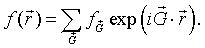
The Fourier coefficients fG are given by,
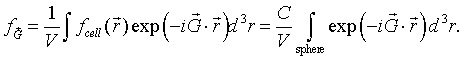
As long as the spheres do not overlap, a primitive unit cell can be defined so that the sphere at the origin lies entirely within the primitive unit cell. Since the function f is zero outside sphere, we just need to integrate over the sphere.
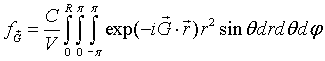
The integral over φ is easily performed.
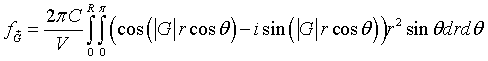
Recognizing that,

the integral over θ can be performed.
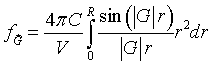
Finally, performing the integral over r,
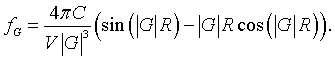
As long as the spheres do not overlap, the Fourier series for spheres repeated on any Bravais lattice is,
