PHY.K02UF Molecular and Solid State Physics
|
| ||||
PHY.K02UF Molecular and Solid State Physics | ||||
A periodic function consists of a primitive unit cell that is repeated on a Bravais lattice. There are five Bravais lattices in two dimensions.
 Oblique |  Rectangular |  Centered rectangular |  |
 |
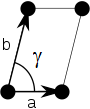
A Bravais lattice can be specified by giving two primitive lattice vectors, $\vec{a}_1$ and $\vec{a}_2$. The lattice parameters (or lattice constants) in two dimensions are the lengths of the primitive lattice vectors $a = |\vec{a}_1|$, $b=|\vec{a}_2|$, and the angle $\gamma$ between the primitive lattice vectors, $\cos\gamma = \vec{a}_1\cdot\vec{a}_2/(ab)$. For convenience $\vec{a}_1$ can be chosen to point in the $x-$direction,
$$\vec{a}_1 = a\,\hat{x},\qquad\vec{a}_2 = b\cos\gamma\,\hat{x} + b\sin\gamma\,\hat{y}.$$The primitive lattice vectors in reciprocal space can then be calculated using the conditions,
$$\vec{a}_i\cdot\vec{b}_j=2\pi\delta_{ij}.$$The primitive lattice vectors in reciprocal space are,
$$\vec{b}_1 = \frac{2\pi}{a}\,\hat{k_x}-\frac{2\pi\cos\gamma}{a\sin\gamma}\,\hat{k_y},\qquad\vec{b}_2 = \frac{2\pi}{b\sin\gamma}\,\hat{k_y}.$$A Fourier series can be used to describe a periodic function in two dimensions. The expression for a Fourier series is,
$$f(\vec{r})=\sum \limits_{\vec{G}} f_{\vec{G}}\exp \left(i\vec{G}\cdot\vec{r}\right).$$The reciprocal lattice vectors are $\vec{G}_{\nu_1,\nu_2}=\nu_1\vec{b}_1+\nu_2\vec{b}_2$, where $\nu_1$ and $\nu_2$ are integers. The Fourier coefficients can be specified with the same integers $f_{\nu_1,\nu_2}=f_{\vec{G}_{\nu_1,\nu_2}}$
A two-dimensional periodic function is plotted below. The form can be used to adjust the ratio $b/a$ and the angle $\gamma$. It is possible to specify four Fourier coefficients $f_{\nu_1,\nu_2}$. The Fourier coefficients are set such that $f_{\vec{G}} = f^*_{\vec{G}}$ so that the periodic function is real. All other Fourier coefficients are set to zero.
|
$\vec{a}_1=1\,\hat{x}$ $\vec{a}_2=$ $\hat{x} + ($ $) \hat{y}$ $\vec{b}_1=$ $\hat{k}_x + ($ $)\hat{k}_y$ $\vec{b}_2=$ $ \hat{k}_y$ |
If all of the Fourier coefficients $f_{\vec{G}}$ have the same value, the resulting periodic function has a peak at every Bravais lattice point. This is the analog to the comb function in one dimension.
Determining the Fourier coefficients
If the periodic function $f(\vec{r})$ is known, the Fourier coefficients $f_{\vec{G}}$ can be determined by multiplying both sides of a Fourier series by $\exp (-i\vec{G}'\cdot \vec{r})$ and integrating over a primitive unit cell.
$$\int\limits_{\text{unit cell}}f(\vec{r})\exp (-i\vec{G}'\cdot \vec{r})d\vec{r} = \sum\limits_{\vec{G}}\int\limits_{\text{unit cell}}f_{\vec{G}}\exp (-i\vec{G}'\cdot \vec{r})\exp (i\vec{G}\cdot \vec{r})d\vec{r}$$On the right-hand side, only the term where $\vec{G} = \vec{G}'$ contributes and the integral evaluates to $f_{\vec{G}}$ times the volume $V_{\text{uc}}$ of the primitive unit cell.
$$f_{\vec{G}} = \frac{1}{V_{\text{uc}}}\int\limits_{\text{unit cell}}f(\vec{r})\exp (-i\vec{G}\cdot \vec{r})d\vec{r} $$Example 1: Checkerboard pattern
Consider a two-dimensional function that has a constant value $C$ on the black squares of a checkerboard and has a value 0 on the white squares of a checkerboard. The lattice constant $a$ is from the center of a black square to the center of a neighboring black square so the sides of a black square are $\sqrt{2}a/2$. This is a two-dimensional analog to the square wave problem that was solved in one dimension.

This function can be expressed as a Fourier series,
$$f(\vec{r})=\sum \limits_{\vec{G}} f_{\vec{G}}\exp \left(i\vec{G}\cdot\vec{r}\right).$$We choose the origin to be in the middle of one of the black squares. The Wigner-Seitz cell contains one black square so we integrate over the square to determine the Fourier coefficients,
$$f_{\vec{G}} = \frac{C}{a^2}\int\limits_{-\sqrt{2}a/4}^{\sqrt{2}a/4}\int\limits_{-\sqrt{2}a/4}^{\sqrt{2}a/4}\exp (-i\vec{G}\cdot \vec{r})dxdy. $$By rewritting the exponential factor,
$$f_{\vec{G}} = \frac{C}{a^2}\int\limits_{-\sqrt{2}a/4}^{\sqrt{2}a/4}\int\limits_{-\sqrt{2}a/4}^{\sqrt{2}a/4}\exp (-iG_xx)\exp (-iG_yy)dxdy, $$the integrals can easily be performed,
$$f_{\vec{G}} = \frac{C}{a^2}\frac{\left(\exp (-iG_x\sqrt{2}a/4)-\exp (iG_x\sqrt{2}a/4)\right)\left(\exp (-iG_y\sqrt{2}a/4)-\exp (iG_y\sqrt{2}a/4)\right)}{-G_xG_y}. $$Using Euler's formula,
$$f_{\vec{G}} = \frac{C}{a^2}\frac{\left(\cos (-G_x\sqrt{2}a/4)+i\sin (-G_x\sqrt{2}a/4)-\cos (G_x\sqrt{2}a/4)-i\sin (G_x\sqrt{2}a/4)\right)\left(\cos (-G_y\sqrt{2}a/4)+i\sin (-G_y\sqrt{2}a/4)-\cos (G_y\sqrt{2}a/4)-i\sin (G_y\sqrt{2}a/4)\right)}{-G_xG_y}. $$The cosine terms cancel out and the final result is,
$$f_{\vec{G}} = \frac{4C}{a^2}\frac{\sin (G_x\sqrt{2}a/4)\sin (G_y\sqrt{2}a/4)}{G_xG_y}. $$
Example 2: circles on a 2-d Bravais lattice
Consider a periodic function defined by non-overlapping circles arranged on a 2-D Bravais lattice.

A function $f$ is defined such that it has a constant value $C$ inside the circles and is zero outside the circles. As long as the circles do not overlap, a primitive unit cell can be defined so that the circle at the origin lies entirely within the primitive unit cell. Since the function $f$ is zero outside circle, we just need to integrate over the circle. The Fourier coefficients $f_{\vec{G}}$ are given by,
$$f_{\vec{G}} = \frac{C}{V_{\text{uc}}}\int\limits_{\text{circle}}\exp (-i\vec{G}\cdot \vec{r})d^2r = \frac{C}{V_{\text{uc}}}\int\limits_{0}^R\int\limits_{-\pi}^{\pi}\left(\cos (|G|r\cos\theta)- i\sin(|G|r\cos\theta)\right)rd\theta dr$$Here $R$ is the radius of the circle. Performing the integral over $\theta$.
$$f_{\vec{G}} = \frac{2\pi C}{V_{\text{uc}}}\int\limits_{0}^RrJ_0(|G|r)dr$$Here $J_0$ is the zeroth order Bessel function. Integrating over $r$ yields,
$$f_{\vec{G}} = \frac{2\pi C}{V_{\text{uc}}}\frac{RJ_1(|G|R)}{|G|}$$Here $J_1$ is the first order Bessel function. As long as the circles do not overlap, the Fourier series for circles repeated on any 2-D Bravais lattice is,
$$f(\vec{r})=\frac{2\pi CR}{V_{\text{uc}}}\sum \limits_{\vec{G}} \frac{J_1(|G|R)}{|G|}\cos \left(i\vec{G}\cdot\vec{r}\right).$$The sine terms cancel out since $f(\vec{r})$ is an even function.