PHY.K02UF Molecular and Solid State Physics
|
| ||||
PHY.K02UF Molecular and Solid State Physics | ||||
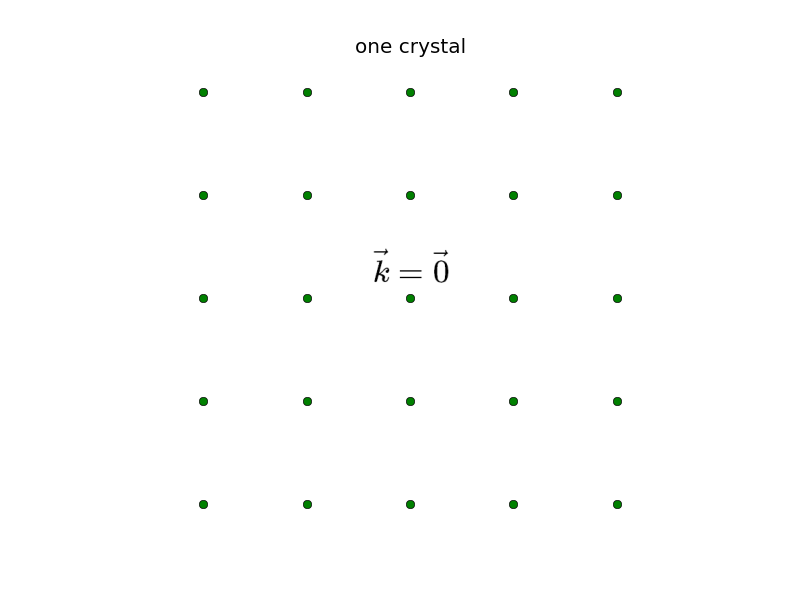
If one imagines one perfect, infinite sized monocrystal, the Fourier transformation of the electron-density $\widetilde{n}\left(\vec{k}\right)=\mathcal{F}\left(n\left(\vec{r}\right)\right)$ has (as every other real valued physical property) only contributions at discrete points on the reciprocal lattice and vanishes everywhere else. Therefore, it can easier be described by a Fourier series:
$n\left(\vec{r}\right)=\displaystyle\sum_{\vec{G}} n_{\vec{G}}e^{i\vec{G}\cdot\vec{r}}$ with $\widetilde n\left(\vec{k}\right)=\displaystyle\sum_{\vec{G}}n_{\vec{G}}\delta\left(\vec{k}-\vec{G}\right)$
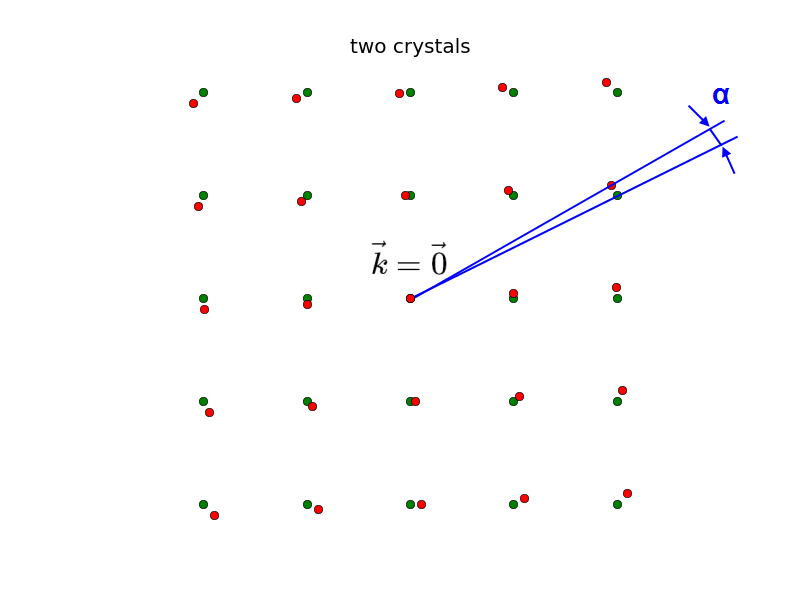
If we put a second crystal of the same material, but with different grid orientations next to each other (we neglect boundary effects due to the finite size of real crystals), the Fourier transformation of the actual electron density (which is the sum of each alone) is also the sum of each Fourier transformation alone:
$n\left(\vec{r}\right)=n_{1}\left(\vec{r}\right)+n_{2}\left(\vec{r}\right) => \widetilde n\left(\vec{k}\right)=\mathcal{F}\left(n\left(\vec{r}\right)\right)=\widetilde{n_{1}}\left(\vec{k}\right)+\widetilde{n_{2}}\left(\vec{k}\right)$
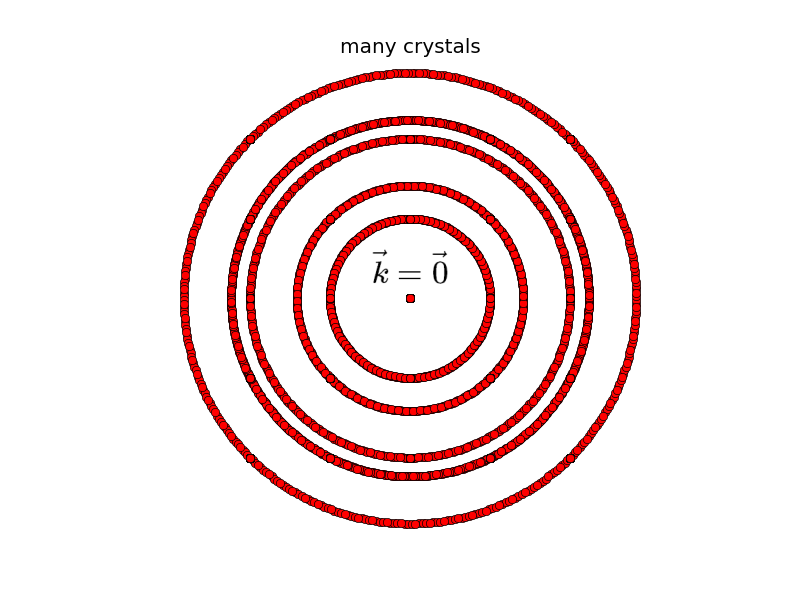
At $\vec{k}=\vec{0}$, the contributions of $n_{1}\left(\vec{k}\right)$ and $n_{2}\left(\vec{k}\right)$ must overlap, but the other points are different due to the different orientations of the crystal. If we now put more and more crystals with different orientations next to each other, the Fourier transformation of the many-crystal electron density will look like spheres around $\vec{k}=\vec{0}$. In practice, this process of putting the crystals in random orientations is made by grinding the single crystal into powder, or in case of a normal metal, by just taking the metal, because it already consists of tiny and random oriented crystals, called grains.
$\widetilde n\left(\vec{k}\right)$ viewed from reciprocal space
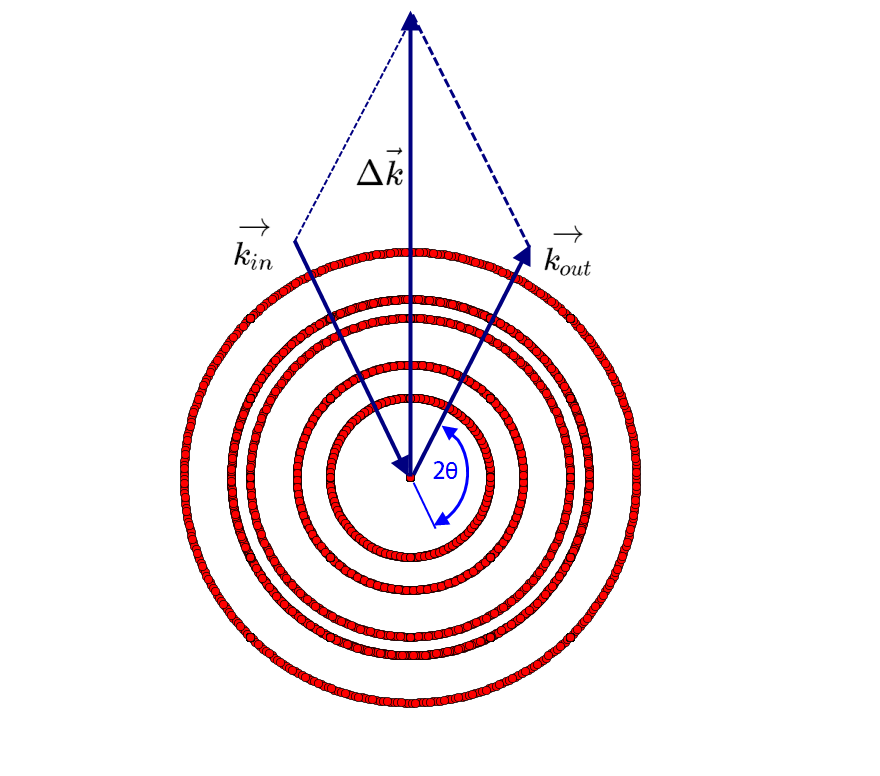
If we want to analyze the powder, we can shoot with an x-ray beam onto it in the direction $\vec{k_{in}}$ and measure the intensity of one of the outgoing beams in the direction $\vec{k_{out}}$. If $\Delta{\vec{k}}$ lands onto a nonzero point of $\widetilde n\left(\Delta{\vec{k}}\right)$, the Bragg condition is fulfilled and we get a high intensity at the detector. The big deal with powder diffraction is now, that the orientation of the powder is of course irrelevant and no exact alignment is necessary. The length of $\Delta{\vec{k}}$ can be varied between 0 and $2|\vec{k}|$ by just moving the detector with $2\theta$ between 0 and 180 degrees.