PHY.K02UF Molecular and Solid State Physics
|
| ||||
PHY.K02UF Molecular and Solid State Physics | ||||
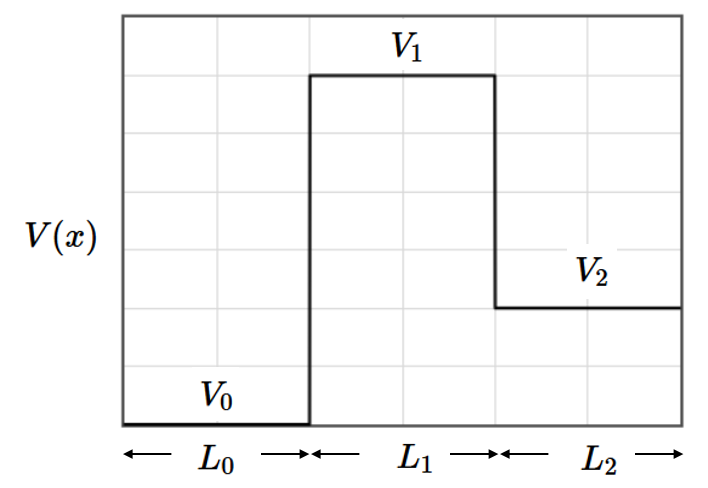
Consider a particle in a piecewise constant potential. The potential has a constant value $V_0$ for a distance $L_0$, $V_1$ for a distance $L_1$, etc.
The time-independent Schrödinger equation for the motion of particle in this potential is,
$$-\frac{\hbar^2}{2m}\frac{d^2\psi}{dx^2}+V(x)\psi=E\psi.$$In a region where the potential has a constant value $V_n < E$, the solutions will have the form,
$$\psi (x) = C_1\cos(k_n(x-x_0))+ C_2\sin(k_n(x-x_0)),$$where
$$k_n = \frac{\sqrt{2m(E-V_n)}}{\hbar}.$$If the wave function and its derivative are known at position $x_0$, then the constants $C_1$ and $C_2$ can be determined.
$$\psi (x_0) = C_1\cos(k_n(x_0-x_0))+ C_2\sin(k_n(x_0-x_0)),$$ $$\frac{d\psi (x_0)}{dx} = -k_nC_1\sin(k_n(x_0-x_0))+ k_nC_2\cos(k_n(x_0-x_0)),$$thus,
$$C_1 = \psi (x_0), \qquad C_2 = \frac{1}{k_n}\frac{d\psi (x_0)}{dx}.$$The equations for $\psi(x)$ and its derivative can be put in matrix form,
$$\begin{bmatrix} \psi(x)\\ \frac{d\psi(x)}{dx} \end{bmatrix} = \begin{bmatrix} \cos(k_n(x-x_0)) & \frac{\sin(k_n(x-x_0))}{k_n}\\ -k_n\sin(k_n(x-x_0)) & \cos(k_n(x-x_0)) \end{bmatrix} \begin{bmatrix} \psi(x_0)\\ \frac{d\psi(x_0)}{dx} \end{bmatrix}.$$For $V_n > E$, the solutions to the Schrödinger equation can be expressed in terms of hyperbolic functions,
$$\psi (x) = C_1\cosh(\kappa_n(x_0-x_0))+ C_2\sinh(\kappa_n(x_0-x_0)),$$where
$$\kappa_n = \frac{\sqrt{2m(V_n-E)}}{\hbar}.$$In this case, if the wave function and its derivative are known at position $x_0$, the wave function throughout the region where the potential is constant is given by the matrix equation,
$$\begin{bmatrix} \psi(x)\\ \frac{d\psi(x)}{dx} \end{bmatrix} = \begin{bmatrix} \cosh(\kappa_n(x-x_0)) & \frac{\sinh(\kappa_n(x-x_0))}{\kappa_n}\\ \kappa_n\sinh(\kappa_n(x-x_0)) & \cosh(\kappa_n(x-x_0)) \end{bmatrix} \begin{bmatrix} \psi(x_0)\\ \frac{d\psi(x_0)}{dx} \end{bmatrix}.$$These matrix equations can be used to solve a number of problems where a quantum particle moves in a piecewise constant potential such as reflections from a potential step, tunneling through a rectangular barrier, a finite potential well, and the Kronig-Penny model. A general solver for a piecewise potential with three levels is shown below. It is necessary to specify the wave function and its derivative at one position. This position is arbitrarily chosen to be the transition between $V_1$ and $V_2$ at $x=0$.
| $E$ [eV] | $\psi$ | |
$x$ Å |
10 Å-1 10 Å-1 10 Å-1