
The translation operator of a periodic system T translates the crystal by a lattice constant a. The matrix representation of the translation operator for a crystal of N = 6 unit cells with periodic boundary conditions is,

When T acts on a vector which specifies some quantity at every unit cell in the crystal, all of the elements of the vector get shifted by one position. Applying the translation operator twice shifts the elements two positions and applying it N times leaves the vector unchanged because all of the elements get shifted back to their original positions. TN is the identity matrix.

The inverse of the translation operator is TN - 1.
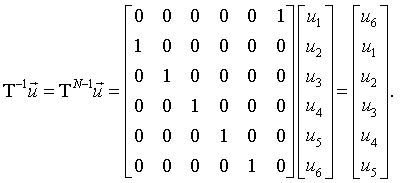
Since TN is the identity matrix and every vector is an eigenvector of the identity matrix with eigenvalue 1, the eigenvalues λ of T have the properties,

Therefore the N eigenvalues of T lie on the unit circle.

The eigenvectors of T have the form,
N even | N odd |
 |  |
This can be checked by applying the translation operator to the eigenvectors. For the case of N = 6,

where the identity ei2πj = 1 was used to get the final form of the vector. The eigenvectors of T², T³,...TN are the same as the eigenvectors of T.
The eigenvectors of the translation operator can be put in one-to-one correspondence with the N allowed k-vectors in the first Brillouin zone of the crystal.

When the elements of the eigenvectors are plotted as a function of position, the correspondence to between the eigenvectors and the allowed k-values is clearly seen. This is illustrated below for N = L/a = 6. The points are the real (red) and imaginary (blue) parts of elements of the eigenvectors. The solid lines are the real and imaginary parts of eikx.


The using this correspondence, the eigenvalues and eigenvectors of the translation operator can be expressed in terms of the allowed values of k in the first Brillouin zone.

The eigenvectors of the translation operator can be used to solve some problems that have translational symmetry. Two examples are given below.
Consider a one-dimensional chain of identical masses of mass m connected by identical springs with spring constant C.

Newton's law for the displacement us of mass s away from its equilibrium position is

We seek the normal mode solutions. In a normal mode all of the components of the mode move with the same frequency.

Here As is the amplitude of the motion of mass s. Substituting this form into Newton's law yields a set of linear equations for the amplitudes,

This set of equations can be written in matrix form. For example, if there are 6 masses in the chain and periodic boundary conditions are applied, the matrix is,
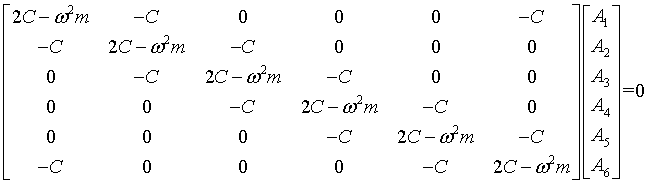
The eigenvectors of this matrix are the normal modes. This matrix can be written in terms of the translation operator,

Here I is the identity matrix, T is the translation matrix and T-1 is the inverse of the translation matrix. The matrices I, T, and T-1 all have the same eigenvectors. These must also be the eigenvectors of the matrix that describes the mass-spring problem. We multiply this matrix by the eigenvectors to determine the eigenvalues.

The condition that the eigenvalues must satisfy is,

Solving for ω yields the dispersion relation for a linear chain,

Below the solid line is the dispersion relation for a linear chain of masses and springs. The dots are the frequencies and k values that correspond to a chain of 6 masses.
