3e tunneling processes in a superconducting single-electron tunneling transistor

PHYSICAL REVIEW B

VOLUME 58, NUMBER 23

15 DECEMBER 1998-I

3e tunneling processes in a superconducting single-electron tunneling transistor

P. Hadley, E. Delvigne, E. H. Visscher, S. Lähteenmäki,and J. E. Mooij
Applied Physics and DIMES, Delft University of Technology
Lorentzweg 1, 2628 CJ Delft, The Netherlands
(Received 11 June 1998)

The American Physical Society.

PACS numbers: 73.23.Hk, 74.50.+r, 85.30.Wx, 85.25.Na

A superconducting single-electron tunneling (SET) transistor consists of a small superconducting island that is coupled to three leads, a gate and two output leads. The two output leads are connected to the island by tunnel junctions and the gate is capacitively coupled to the island. The quantum nature of this device is manifested in the periodic modulation of the current that flows through the output leads as the charge on the gate is varied. One modulation period corresponds to adding one electron charge e to the island. By monitoring the current one can make very sensitive measurements of the charge at the gate. The charge sensitivity of a SET transistor in the superconducting state is better than the charge sensitivity of a SET transistor in the normal state which makes the superconducting SET transistor the most sensitive device now available for measuring charge. [1,2]

The characteristics of a superconducting SET transistor depend on the relative magnitudes of three energies: the charging energy E_C, the Josephson energy E_J, and the superconducting gap Δ. [3] The charging energy is the energy associated with charging the island witha single electron charge, E_C = e²/(2C_S). Here C_Sis the total capacitance of the island. The Josephson energy is related to the junction critical current I_c, E_J= hI_c/(4pe),and the superconducting gap can be seen as the addition energy that is required for a superconducting island to have an odd number of electrons rather than an even number of electrons.[4] In devices with large junctions, the Josephson energy is much larger than the charging energy, E_J >> E_C, and a supercurrent is observed. As the junctions are made smaller, E_Jdecreases while E_C increases. When E_J ~ E_Cthe supercurrent can be modulated by applying a voltage to the gate, whileforE_J << E_Cthe supercurrent is suppressed. If D>E_C > E_Jparity effects are observed.[5] Itis then possible to determine if the number of electrons on the islandis an odd or even number. In the present experiment D~ E_C >> E_Jand no supercurrent was observed.

The SET transistor studied consisted of two Al/AlO_x/Al tunnel junctions that were fabricated by shadow evaporation. The two junction capacitances were C₁ = 2.1 x10^-16 F and C₂=1.8 x 10^-16F, the gate capacitance was C_g =1.2 x 10^-18F, and the total resistance of the device was R₁+ R₂ = 1.7 x 10⁶W. Under normal operating conditions, the current that flows through a superconducting SET transistor is primarily due to the sequential tunneling of normal quasiparticles. However, at low bias voltages, the tunneling of individual quasiparticles is suppressed by a combination of the Coulomb blockade and the absence of states in the superconducting gap. At these low bias voltages, other transport mechanisms can be observed such as cotunneling, [6] the Josephson - quasiparticlecycle, [7] and singularity matching [8]. Here we report the experimental observation of a current that flows due to the simultaneous tunneling of a Cooper pair and a quasiparticle. The Cooper pair and the quasiparticle simultaneously tunnel through two different tunnel barriers that are spaced about 0.5 μm from each other.

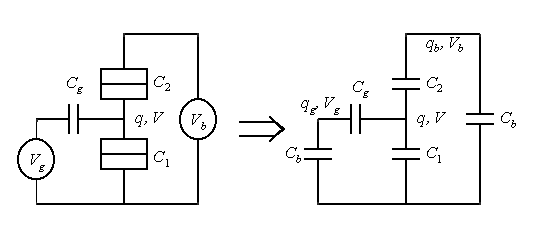
The thresholds for the various tunnel events that occur in a SET transistor can be determined by examining the electrostatic energy of the circuit. To calculate the change in electrostatic energy when an electron tunnels, one can treat the circuit as a network of capacitors. It is convenient to also treat the voltage sources as capacitors with very large capacitances. At the end of the calculation the limit of very large capacitance for the voltage sources is taken. Figure 1 shows the equivalent capacitor network for an asymmetrically biased SET transistor.

Fig. 1 The equivalent capacitor network used to calculate the electrostatic energy of a SET transistor.

The electrostatic energy of this network of capacitors is the sum of the electrostatic energies of the capacitors,

$\begin{displaymath}E=\frac{1}{2}C_1V^2+\frac{1}{2}C_2\left( V-V_b\right) ^2+\fra......V-V_{g}\right) ^2+\frac{1}{2}C_bV_{b}^2+\frac{1}{2}C_bV_{g}^2.\end{displaymath}$

(1)

Taking the derivatives of the electrostatic energy with respect to the three voltages (V,V_b,V_g) yields a set of three coupled equations which can be written in the form

$q_i=\frac{\partial E}{\partial V_{i}}=\sum_{j}C_{ij}V_{j}$ .Here q_i are the charges on the islands and C_ijis the capacitance matrix. The electrostatic energy of the circuit canthen be rewritten as [9] $E=\frac{1}{2}\sum_{i,j}C_{ij}^{-1}q_{i}q_{j}$ .This form was used to calculate the change in electrostatic energy when charge tunneled. Figure 2 illustrates the tunnel eventsthat were considered. Each arrow indicates that a charge of e has passed through that tunnel junction.

Fig. 2 Nine tunnel processes were observed in the experiment. Each arrow indicates that a charge ofe has passed through that junction.

In the limit C_b>>C₁,C₂,C_g,the changes in the electrostatic energies are,

$\begin{mathletters}% latex2html id marker 84\begin{equation}\delta E=\frac{e}......2C_{1}+C_2+2C_g \right) V_{b}+C_{g}V_{g}\right].\end{equation}\end{mathletters}$

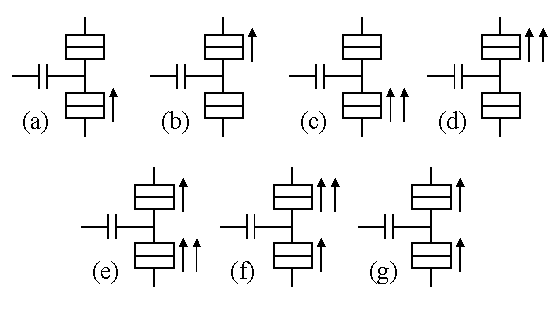
Equation 2x corresponds to the tunnel event illustrated in Fig. 2x.The changes in electrostatic energy can be used to construct a stability diagram for the superconducting SET transistor as shown in Fig. 3.

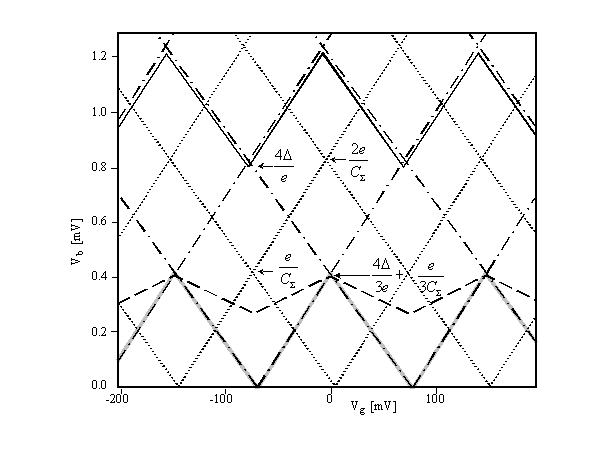
Fig. 3. The thresholds forvarious tunnel processes in a superconducting SET transistor as a function of gate voltage and bias voltage. The solid line is the threshold for sequential quasiparticle tunneling (Fig. 2a and Fig.2b, dE= -2D),the dot - dash lines are the thresholds for singularity matching (Fig.2a and Fig. 2b, dE= 0) and coincide with the threshold for the Coulomb blockade in the normalstate (gray line). The dotted lines are the thresholds for tunnel events involving Cooper pair tunneling (Fig. 2c and Fig. 2d, dE= 0). The dashed lines are the thresholds for the tunneling of 3eof charge (Fig. 2e and Fig. 2f, dE= -2D).The experimental values were used to generate this figure. The program that was used to generate the figure is available at http://med.tn.tudelft.nl/~hadley/set/stability/stability.html

Each line in Fig. 3 represents the threshold for a certain tunnel process. The position of the threshold is dependent on the number of electrons on the island, n. This results in a periodicstability diagram with a periodicity e. The lines which are determined by the tunneling of charge only through junction 1 (Fig. 2aand Fig. 2c) have a slope of -C_g/C₂.The lines which are determined by the tunneling of charge only through junction 2 (Fig. 2b and Fig. 2d)have a slope of C_g/(C₁+C_g).The threshold determined by the tunneling of 3e of charge as shownin Fig. 2e has a slope of -C_g/(C₁+2C₂+C_g)and the slope of the threshold determined by the tunnel process shown in Fig. 2f is C_g/(2C₁+C₂+2C_g).Figure 4 shows the measured currentthrough the superconducting SET transistor as a function of the bias voltage and the gate voltage.

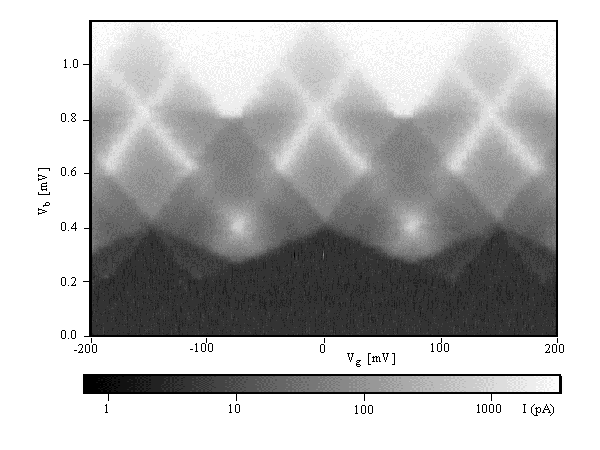
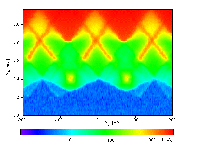
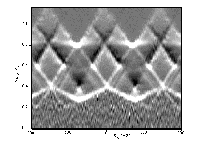
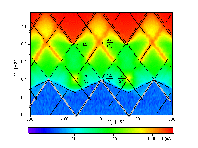
Fig. 4. The logarithm of the current through a superconducting SET transistor is plotted as a function of the bias voltage and the gate voltage. The same data plotted in color,the derivative d(log(I))/dV_bof the same data, or a comparison of the color version and Fig. 3 can beviewed by clicking on one if the three images below.

The logarithm of the current was taken so that the high bias data and low bias data could be presented in the same figure. The current is periodic in gate voltage with a periodicity of e/C_g.The inverted white triangles at the top of Fig. 4form the threshold for sequential quasiparticle tunneling through the SETtransistor. In this process, a single quasiparticle tunnels onto the island through one junction and then another quasiparticle tunnels out through the other junction. These tunnel processes are shown in Fig. 2aand and Fig. 2b (dE= -2D). The minimum bias voltage for the threshold for sequential quasiparticle tunneling is 4D/eand the maximum is 4D/e + e/C_S.Here C_Sis the total capacitance, C_S= C₁+ C₂+ C_g. The changein electrostatic energy when a quasiparticle tunnels must be dE= -2D because there are no quasiparticle stateswithin the superconducting gap.

Also clearly visible in Fig. 4 are intersectinglines of current that are due to the Josephson - quasiparticle (JQP) cycle.These are the white Xs centered at about 0.8 mV. In this transport mechanism,first a Cooper pair tunnels onto the island through one junction and then two normal quasiparticles tunnel through the other junction. For the JQPcurrent line with a negative slope in the V_b-V_gplane, first a Cooper pair tunnels (Fig. 2c, dE= 0) and then two quasiparticles tunnel sequentially (Fig. 2b,dE = -2D).For the JQP current line with a positive slope in the V_b- V_g plane, the sequence is (Fig.2d, dE = 0) and thentwice (Fig. 2a, dE= -2D). The JQP lines intersect at a bias voltageof 2e/C_S.

The horizontal line at 4D in Fig. 4is due to the rather abrupt onset of cotunneling of quasiparticles at a bias voltage of 4D. This cotunneling is illustratedin Fig. 2g. Cotunneling of quasiparticles for bias voltages less than 4D is suppressed by the lack of quasiparticle states in the superconducting gap.[10]

There are also isolated current peaks located at a bias of 0.4 meV inFig. 4. These peaks lie on the extensions of the JQPlines at a bias voltage of e/C_S.[11,12] Four sequential tunneling events are responsible for these current peaks. The sequence of tunnelevents is (Fig. 2c, dE= 0), (Fig. 2b, dE= -2D), (Fig. 2d, dE= 0), (Fig. 2a, dE= -2D). The first and the third events involve the tunneling of Cooper pairs while in the second and fourth events quasiparticles tunnel.

Now we focus on the sawtooth threshold for current that lies just below 0.4 mV in Fig. 4. This threshold is e periodic and the lines that form the threshold have a slope that is one third ofthe slope of the threshold for sequential quasiparticle tunneling or the JQP lines. The tunnel process responsible for this threshold is one where a Cooper pair and a quasiparticle tunnel simultaneously. This sort of cotunneling event involving a Cooper pair and a quasiparticle was first described by Maassen van den Brink et al. [13] First the charge on the island decreases by -e via the tunnel event shown in Fig.2e with dE = -2D.Then the island returns to its initial charge state via the tunnel eventin Fig. 2f with dE= -2D. The minimum bias voltage for this threshold is 4D/3e and the maximum bias voltage for this threshold is for this process is 4D/3e+ e/(3C_S). A similar simultaneous 3e tunneling threshold should also occur for SET transistors in the normal state (Fig. 2e andFig. 2f, dE = 0). However in that case three particles would have to tunnel simultaneously so the rate would be much lower.

The tunneling of 3e of charge also forms part of a sequence of tunnel events that is responsible for the current observed in the diamond shaped regions that extend from a bias voltage of about 0.4 mV to 1.2 mV. In this region, first 3e of charge tunnels as in Fig. 2e(or Fig. 2f) with dE= -2D. Then the charge of the island returns to its initial state by the tunneling of a quasiparticle as in Fig. 2b(or Fig. 2a) with dE= -2D.

At bias voltages between 0.2 mV and 0.4 mV a small current that is 2eperiodic is observed. This current arises from the sequential tunneling of a quasiparticle and the tunneling of 3e of charge as described above. If the initial state of the island is odd, then a quasiparticle can tunnel on or off the island in the tunnel processes illustrated in Fig. 2a or Fig. 2b with dE= 0. [14] In this tunnel process, the quasiparticle that tunnels pairs with the odd quasiparticle on the island. The island then returns to its initial charge state via a Cooper pair-quasiparticle cotunneling event (Fig. 2e or Fig. 2f,dE = -2D). A similar process cannot occur if the initial state of the island is even since the quasiparticle that tunnels from the lead has no partner to condense with to form a Cooper pair. Consequently, this current is 2e periodic.

In summary, the thresholds for a number of distinct charge transport mechanisms were observed in the current-voltage characteristics of a superconducting SET transistor. These cycles involve the sequential tunneling of quasiparticles, the sequential tunneling of Cooper pairs and quasiparticles (JQP Cycles), cotunneling of quasiparticles, and the sequential cotunneling of Cooperpairs and quasiparticles with the tunneling of quasiparticles. Of particular interest are the currents that arise from cycles which include cotunneling of a Cooper pair and a quasiparticle. In this tunnel process, a charge of 3e tunnels and the Cooper pair and quasiparticle are transported simultaneously through two different tunnel barriers. Cotunneling of a Cooper pair and a quasiparticle also plays a role in a sequence of tunnelevents that leads to a 2e periodic current at low bias voltages.

ACKNOWLEDGMENTS

We are indebted to Leonid Glazman, Yuli Nazarov, Gerd Schön, andArcadi Odintsov their enlightening comments on this work. Support fromEsprit project 22953, CHARGE, is gratefully acknowledged.

REFERENCES

1. A. N. Korotkov, Appl. Phys. Lett. 69 2593(1996).

2. R.J. Schoelkopf, P. Wahlgren, A. A. Koshevnikov,P. Delsing, and D. E. Prober, Science, accepted for publication.

3. M. Tinkham, Introduction to Superconductivity,(McGraw-Hill, New York, 1996).

4. D. V. Averin, and Yu. V. Nazarov, Phys. Rev. Lett.69 1993 (1992).

5. M. T. Tuominen, J. M. Hergenrother, T. S. Tighe,and M. Tinkham, Phys. Rev. Lett. 69 1997 (1992).

6. D. V. Averin and K. K. Likharev, in MesoscopicPhenomena in Solids, eds. B. L. Altshuler, P. A. Lee, and R. A. Webb,Elsevier (1991).

7. T. A. Fulton, P. L. Gammel, D. J. Bishop, L. N.Dunkleburger, and G. J. Dolan, Phys. Rev. Lett. 63 1307 (1989).

8. Y. Nakamura, A. N. Korotkov, C. D. Chen, and J.S. Tsai, Phys. Rev. B. 56 5116 (1997).

9. J. D. Jackson, Classical Electrodynamics, (JohnWiley and Sons, New York, 1975).

10. D. V. Averin, A. N. Korotkov, A. J. Manninen,and J. P. Pekola, Phys. Rev. Lett. 78 4821 (1997).

11. A. Maassen van den Brink, A. A. Odintsov, P.A. Bobbert, and G. Schön, Zeitschrift für Physik B 85 459 (1991).

12. Jens Siewert and Gerd Schön, Phys. Rev.B, 54 7421 (1996).

13. Alec Maassen van den Brink, Gerd Schön,and L. J. Geerligs, Phys. Rev. Lett. 67 3030 (1991).

14. G. Schön, J. Siewert, and A. D. Zaikin,Physica B 203 340 (1994).