Energieerhaltungssatz
Energie bleibt erhalten. Sie kann umgewandelt werden in verschiedenen Formen, kinetische, potentielle oder thermische Energie, aber die Gesamtenergie bleibt immer gleich. Die kinetische Energie eines Teilchens ist $E_{kin} = \frac{mv^2}{2}$ [J] wobei $m$ [kg] die Masse des Teilchens ist und $v$ [m/s] seine Geschwindigkeit.
Die geleistete Arbeit ist gleich der Änderung der kinetischen Energie, plus der Änderung der potentiellen Energie, plus der Arbeit die gegen unkonservative Kräfte (Reibungskräfte) geleistet wurde.
Beispiel 1
Eine Masse von 500 g wird auf einem reibungsfreien Tisch platziert und ist an einer nichtlinearen Feder angebracht. Die Kraft, die diese Feder ausübt ist $F=-6x-4x^3$ [N] wobei $x$ in Metern gemessen wird. Die Feder wird zusammengedrückt um 16 cm und anschließend so losgelassen, dass die Anfangsgeschwindigkeit der Masse gleich Null ist. Was ist die Maximalgeschwindigkeit der Masse?
Lösung: In der zusammengedrückten Feder wird potentielle Energie gespeichert. Diese Energie ist $W = \int Fdx = \int\limits_0^{0.16} 6x+4x^3 dx = \left. 3x^2 + x^4\right|_0^{0.16}=0.07745536$ [J]. Da es keine Reibung gibt, wird die gesamte Energie in kinetische Energie $\frac{mv^2}{2}$ umgewandelt. Die maximale Geschwindigkeit ist $v_{max} = 0.5566$ [m/s].
Beispiel 2
Eine Kiste mit der Masse von 14 kg wird 5 m über einen horizontalen Boden mithilfe eines Seiles im 45°-Winkel gezogen, mit einer Kraft von 72 N. Die kinetische Energie der Kiste zu Beginn und die kinetische Energie am Ende sind Null. Während die Kiste über den Boden gezogen wird, erzeugen Reibungskräfte Wärme. Wie viel thermische Energie wird dabei erzeugt?
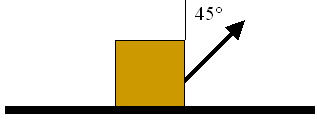
Lösung: Die Änderung der kinetischen Energie und die Änderung der potentiellen Energie ist Null, also wird die Kraft, die benötigt wird um die Kiste zu bewegen, vollständig in thermische Energie umgewandelt. Die Masse der Kiste ist nicht relevant.
$$W = \int\vec{F}\cdot d\vec{r} = 72 \cos(45^{\circ}) 5 = 254.6 \,\, \text{J.}$$