Interferenz an zwei schmalen Spalten
Wenn wir uns die beiden Spalten von weiter weg ansehen, können wir das Interferenzmuster im Fernfeld betrachten. In bestimmten Richtungen kann man konstruktive, in anderen Richtungen destruktive Interferenz beobachten.

Die Interferenz kann berechnet werden bei der Entfernung $L$ von den Spalten und bei einer Höhe $y$ vom Zentrum der Spalte. Der Weg, den die Welle vom oberen Spalt zu diesem Punkt zurücklegt, ist $r_1$, der Weg vom unteren Spalt bis zum Punkt ist $r_2$. Die Differenz zwischen diesen Abständen ist der schmale rote Bereich $r_2-r_1=d\sin\theta$, wobei $d$ der Abstand zwischen den beiden Spalten ist und $\theta \approx \frac{y}{L}$.
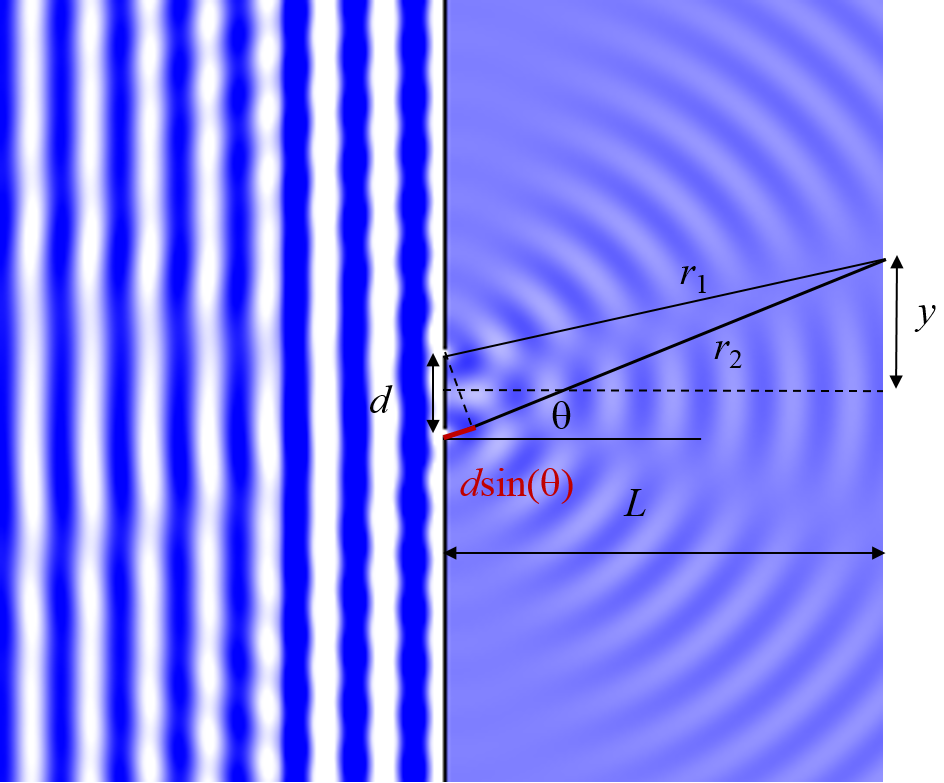
Es entsteht konstruktive Interferenz, wenn $r_2-r_1$ eine ganzzahlige Anzahl von Wellenlängen ist, und destruktive Interferenz, wenn $r_2-r_1$ eine ganzzahlige Anzahl von Wellenlängen plus eine halbe Wellenlänge ist.
Im Fernfeld: $L >> d >> n\lambda$
Konstruktive Interferenz $r_2-r_2=d\sin\theta \approx d\frac{y}{L}=n\lambda$ $n\in$ Ganzzahlen
Destruktive Interferenz $r_2-r_2=d\sin\theta \approx d\frac{y}{L}=\left(n+\frac{1}{2}\right)\lambda$ $n\in$ Ganzzahlen
Erläterung der Simulation (optional)