Eine mit zwei Federn verbundene Masse auf reibungsfreiem Tisch
Systeme mit mehreren Freiheitsgraden können für verschiedene Moden verschiedene Resonanzfrequenzen haben. In der Eigenmode eines Sytems oszillieren alle Komponenten des Systems mit der gleichen Frequenz. Ein einfaches Beispiel ist eine Masse, die durch zwei Federn so verbunden wird, dass sich die horizontalen und vertikalen Oszillationsfrequenzen unterscheiden. Dieses wird im folgenden Video genauer dargestellt.
Die Trajektorie/Bahn der Masse kann berechnet werden, indem die entsprechende Differentialgleichung numerisch integriert wird.
Eine Masse $m$ auf einem reibungsfreien Tisch sei von links und von rechts mit zwei Federn der Federkonstante $k$ verbunden. Die Länge der ungestreckten Feder sei $l$ und die Breite des Tisches sei $w$ mit $w > 2l$.
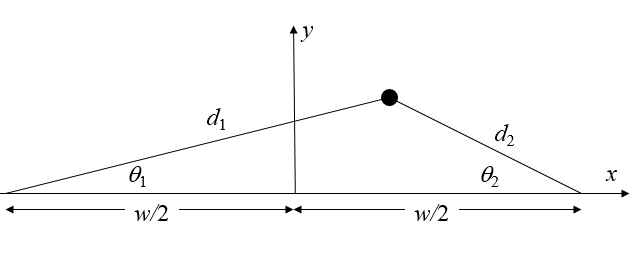
Die Gleichgewichtsposition der Masse liege in der Tischmitte $(x=0,y=0)$, an welcher die von den Federn ausgeuuml;bten Kräfte sich exakt aufheben. Wird die Masse von dieser Gleichgewichtsposition wegbewegt, dann wirkt folgende Kraft auf die Masse
\[ \begin{equation} \vec{F}=k\left[(d_2-l)\cos\theta_2-(d_1-l)\cos\theta_1\right]\hat{x}-k\left[(d_2-l)\sin\theta_2+(d_1-l)\sin\theta_1\right]\hat{y}. \end{equation} \]Hier ist $d_1 = \sqrt{(w/2+x)^2+y^2}$, $d_2 = \sqrt{(w/2-x)^2+y^2}$, $\theta_1=\text{atan}\left(\frac{y}{w/2+x}\right)$ und $\theta_2=\text{atan}\left(\frac{y}{w/2-x}\right)$.
Das folgende Feld berechnet die Trajektorie der Masse, nachdem sie von einer Ruheposition $ (x_0,y_0)$ losgelassen wurde.
|
|