Dünne Linsen: Kleine Winkelnäherung
Durch Experimentieren mit der App für dicke Linsen haben wir gesehen, dass es möglich ist Licht an einen Punkt zu fokussieren, wenn nur die Lichtstrahlen nahe der optischen Achse verwendet werden und die Linse dünn ist $(d << f)$. In diesem Fall ist es zweckmäßig, die Winkel in Bezug auf die horizontale optische Achse zu messen. Für kleine Winkel ist der Winkel in Radiant die Steigung des Lichtstrahls.
Denken Sie sich einen Lichtstrahl, der auf eine Grenzfläche mit einem kleinen Winkel bezüglich der optischen Achse trifft.
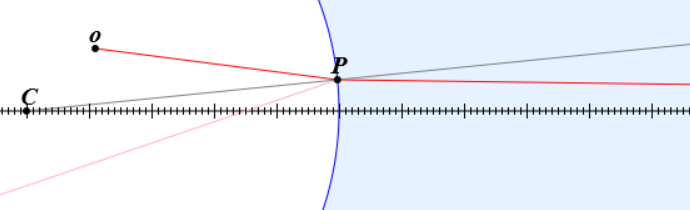
Die Steigung des Strahls links der Grenzfläche ist,
$$\phi_1 = \frac{y_P-y_o}{x_P-x_o}\quad\text{rad}.$$Die Linie $\overline{CP}$ steht normal auf die Grenzfläche. Wenn $|y_P| << |R|$, dann ist die Steigung der Linie normal zur Grenzfläche, $\phi_n \approx -\frac{y_p}{R}$. Der Winkel zwischen dem einkommenden Strahl und der Grenzflächennormale ist,
$$ \theta_1 = \phi_1 - \phi_n\quad\text{rad}.$$Unter Verwendung des Snelliusschen Gesetzes ist es möglich den Winkel zu berechnen, den der Lichtstrahl auf der rechten Seite mit der Grenzflächennormale aufspannt.
$$n_1\sin\theta_1 = n_2\sin\theta_2.$$Da $\phi_1$ und $\phi_n$ kleine Winkel sind, werden $\theta_1$ und $\theta_2$ ebenfalls kleine Winkel sein und wir können die Näherung $\sin(x)\approx x$ verwenden. Die vereinfachte Version des Snelliusschen Gesetzes ist,
$$n_1\theta_1 = n_2\theta_2.$$Auf der rechten Seite der Grenzfläche, kann der Winkel zwischen der Normale und dem Lichtstrahl, $\theta_2$, ausgedrückt werden durch die Steigung der Normale, $\phi_n$, und die Steigung des Lichtstrahls auf der rechten Seite der Grenzfläche, $\phi_2$, $$ \theta_2 = \phi_2 - \phi_n\quad\text{rad}.$$
Diese Gleichung kann gelöst werden für $\phi_2$. Unter Verwendung des vereinfachten Snelliusschen Gesetzes,
|
$\hspace{0.5cm}\large \phi_2 \approx \frac{(n_1-n_2)y_P}{Rn_2}+\frac{n_1}{n_2}\phi_1 \quad$rad.$\hspace{0.5cm}$ |
Diese Näherung für kleine Winkel beschreibt, wie ein Lichtstrahl, mit einem kleinen Winkel bezüglich der optischen Achse, an einer Grenzfläche gebeugt wird. Eine Linse besteht aus zwei Grenzflächen, also muss die Formel zweimal angewendet werden. Denken Sie sich eine Linse mit einem Brechungsindex $n_{\text{lens}}$ in einem Medium mit einem Brechungsindex $n_{\text{env}}$. Die Linse hat den Radius $R_{\text{left}}$ auf der linken Seite und $R_{\text{right}}$ auf der rechten Seite. Die Steigung des Lichtstrahls auf der linken Seite der Linse ist $\phi_{\text{left}}$. Wir gehen davon aus, dass dieser Winkel klein ist. Unter Verwendung der Näherung für kleine Winkel ist die Steigung des Lichtstrahls, nachdem er auf die linke Grenzfläche trifft,
$$ \phi_{\text{lens}} \approx \frac{(n_{\text{env}}-n_{\text{lens}})y_P}{R_{\text{left}}n_{\text{lens}}}+\frac{n_{\text{env}}}{n_{\text{lens}}}\phi_{\text{left}} \quad\text{rad}.$$$ \phi_{\text{lens}} $ ist die Steigung des Strahls in der Linse. Der Strahl trifft dann auf die rechte Grenzfläche. Wir nehmen an, dass die Linse so dünn ist, dass die Entfernung zur optischen Achse, $y_P$, dieselbe bleibt. Die Steigung des Lichtstrahls auf der rechten Seite der Linse ist,
$$ \phi_{\text{right}} \approx \frac{(n_{\text{lens}}-n_{\text{env}})y_P}{R_{\text{right}}n_{\text{env}}}+\frac{n_{\text{lens}}}{n_{\text{env}}}\phi_{\text{lens}} \quad\text{rad}.$$Ersetzen wir $\phi_{\text{lens}}$ mithilfe der Gleichung oberhalb, dann erhalten wir,
$$ \phi_{\text{right}} \approx \frac{(n_{\text{lens}}-n_{\text{env}})y_P}{R_{\text{right}}n_{\text{env}}}+\frac{n_{\text{lens}}}{n_{\text{env}}}\frac{(n_{\text{env}}-n_{\text{lens}})y_P}{R_{\text{left}}n_{\text{lens}}}+\phi_{\text{left}} \quad\text{rad}.$$ $$ \phi_{\text{right}} \approx -\left( \frac{1}{R_{\text{left}}}-\frac{1}{R_{\text{right}}}\right)\frac{(n_{\text{lens}}-n_{\text{env}})y_P}{n_{\text{env}}}+\phi_{\text{left}} \quad\text{rad}.$$Dies kann kompakter geschrieben werden als,
|
$\hspace{0.5cm}\large \phi_{\text{right}} \approx -\frac{y_P}{f}+\phi_{\text{left}} \quad$rad,$\hspace{0.5cm}$ |
wobei $f$ die Brennweite ist,
|
$\hspace{0.5cm}\Large \frac{1}{f} = \left( \frac{1}{R_{\text{left}}}-\frac{1}{R_{\text{right}}}\right)\frac{(n_{\text{lens}}-n_{\text{env}})}{n_{\text{env}}}.\hspace{0.5cm}$ |
Dies nennt man die Linsenschleifer- oder Linsenmacherformel. Meist werden Linsen in Luft verwendet, also $n_{\text{env}}=1$. Die Linsenschleiferformel vereinfacht sich damit zu,
$$\frac{1}{f} = (n_{\text{lens}}-1)\left( \frac{1}{R_{\text{left}}}-\frac{1}{R_{\text{right}}}\right).$$In der Simulation unterhalb wird Licht von einem Objekt $o$ emittiert. Es gibt hier drei interessante Lichtstrahlen. Der erste Strahl, ist der, der das Objekt horizontal verlässt, $\phi_{\text{left}}=0$. Für diesen Strahl ist die Steigung auf der rechten Seite der Linse, $\phi_{\text{right}} \approx -\frac{y_P}{f}$. Für jeden beliebigen Wert von $y_P$ geht dieser Strahl durch den Brennpunkt der Linse. Dieser Brennpunkt ist der blaue Punkt mit der Bezeichnung $f$. Der zweite interessante Strahl ist der Strahl, der das Objekt $o$ verlässt und die optische Achse am Punkt $y_p=0$ durchquert. Für diesen Strahl ist $\phi_{\text{right}} \approx \phi_{\text{left}}$. Dieser Strahl wird von der Linse nicht gebeugt. Der dritte Strahl der uns interessiert, ist der, der das Objekt $o$ verlässt und durch die gespiegelte Abbildung des Brennpunktes, $f'$, geht. Dieser Strahl wird horizontal gebeugt, sodass $\phi_{\text{right}}=0$. Alle drei dieser Strahlen treffen sich an der Abbildung des Objektes, $i$.
Die Brennweite kann sowohl positiv, als auch negativ sein. Sammellinsen haben eine positive Brennweite, welche sich auf der rechten Seite der Simulation befindet. Zerstreuungslinsen haben dagegen eine negative Brennweite, diese befindet sich auf der linken Seite der Linse. Die Abbildung $i$ ist virtuell, wenn die Strahlen selbst nicht durch den rechten Bildpunkt gehen, sondern nur deren virtuelle Verlängerung (pink). Das Bild ist dann virtuell, wenn $f < 0$ oder $f > 0$ und $x_o$ sich näher an der Linse befindet als eine Brennweite.