J. J. Thomson's Experiment um das Ladungs-Massen-Verhältnis von Elektronen zu bestimmen
J. J. Thomson führte Experimente durch, um zu zeigen, dass Atome aus Teilchen bestehen, welche positive und negative Ladungen haben. Er stellte fest, dass die negativ geladenen Teilchen (Elektronen) viel leichter sind, als die positiv geladenen Teilchen. Das Verhältnis von Ladung zu Masse der Elektronen wurde gemessen, durch Beschleunigung von Elektronen durch eine Spannung $V_x$ zu einer positiv geladenen Platte. Einige Elektronen gelangen durch ein kleines Loch in der Platte und bilden einen Elektronenstrahl, der sich durch eine Region bewegt, in der ein elektrisches Feld und ein magnetisches Feld befinden. Die Elektronen wurden in die $x$-Richtung beschleunigt, das elektrische Feld war in der $y$-Richtung und das Magnetfeld in der $z$-Richtung.
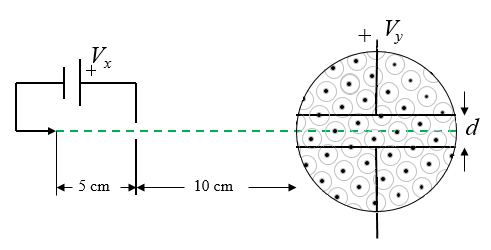
Die Kraft auf ein Elektron, auf Grund des elektrischen Feldes ist $\vec{F}_{\text{elec}}=-|e|E_y\hat{y}$ und die Kraft auf das Elektron, auf Grund des Magnetfeldes $\vec{F}_{\text{magn}}=|e|v_xB\hat{y}$. Die Geschwindigkeit der Elektronen kann festgestellt werden,da diese in $x$-Richtung beschleunigt wurden, und so die potentielle Energie $|e|V_x$ in kinetische, $\frac{1}{2}mv_x^2=|e|V_x$ umgewandelt wird. Deshalb ist $v_x=\sqrt{2|e|V_x/m}$. Wird das Experiment so verändert, dass sich die elektrische und die magnetische Kraft gegenseitig aufheben $|e|v_xB\hat{y}-|e|E_y\hat{y}=0$, ist das Verhältnis zwischen Ladung und Masse gegeben durch,
\[ \begin{equation} \frac{e}{m}=\frac{V_y^2}{2V_x\mu_0^2n^2I^2d^2}. \end{equation} \]Die untere Simulation behinhaltet Metallplatten, welche 10 cm lang sind, mit einem Abstand von $d=$ 2 cm. Die Zylinderspule, die das Magnetfeld erzeugt, hat einen Durchmesser von 10 cm.
|
|