Ampèresche Gesetz
In den vorhergehenden Kapiteln wurde gezeigt, dass, wenn der Strom bekannt ist, das Magnetfeld mithilfe des Biot-Savart Gesetzes berechnet werden kann. Das Ampère'sche Gesetz erlaubt es uns die Ströme ausgehend vom Magnetfeld zu berechnen. Es gibt zwei Arten des Ampère'schen Gesetzes. Die differenzielle Form erlaubt es uns die Stromdichte zu berechnen,
$$\nabla\times\vec{B}=\mu_0 \vec{J}.$$Hier ist die Rotation $\nabla\times\vec{B}$ definiert als,
$$\nabla\times\vec{B}=\left(\frac{\partial B_z}{\partial y}-\frac{\partial B_y}{\partial z}\right)\hat{x}+ \left(\frac{\partial B_x}{\partial z}-\frac{\partial B_z}{\partial x}\right)\hat{y}+ \left(\frac{\partial B_y}{\partial x}-\frac{\partial B_x}{\partial y}\right)\hat{z}.$$Das Ampère'sche Gesetz kann umgeschrieben werden mithilfe des Stokes'schen Satzes in eine Form, die ein Kurvenintegral über die Kurve $C$ des Magnetfeldes in Relation setzt mit dem Strom $I_{enc}$ der durch diese Kurve fließt,
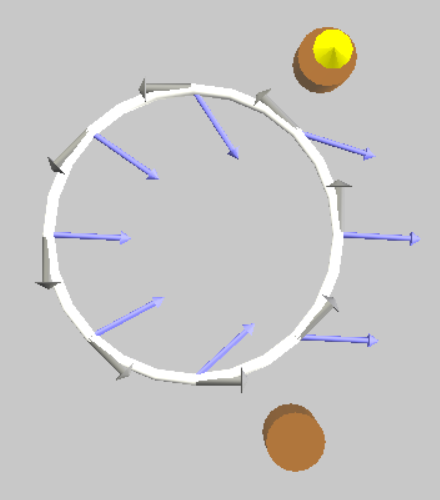
\begin{equation} \oint\limits_{C}\vec{B}\cdot d\vec{l}=\mu_0 I_{enc}. \end{equation}Das Ampère'sche Gesetz kann veranschaulicht werden mit der folgenden Simulation.