Elektrisches Feld einer Oberflächenladungsdichte
Betrachten Sie eine gleichmäßige Ladungsschicht bei $x=0$. Die $y-z$ Ebene enthält Ladungen mit einer Dichte $\sigma$ Coulombs/m². Eine Punktladung an Position $(0,y,z)$ hat eine Ladung $\sigma dydz$.
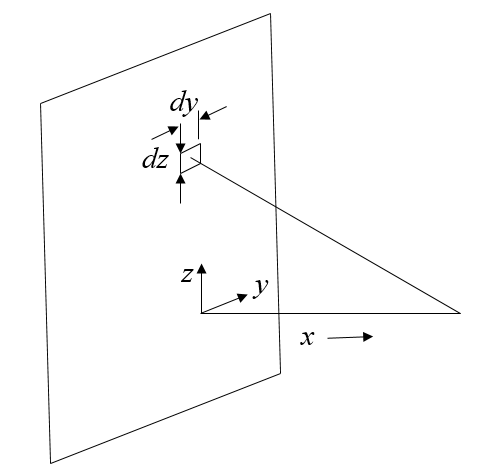
Diese kleine Ladung wird ein kleines elektrisches Feld $d\vec{E}$ zum elektrischen Feld an der Position $x$ beitragen,
$$d\vec{E} = \frac{\sigma dydz}{4\pi\epsilon_0(x^2+y^2+z^2)}\frac{x}{\sqrt{x^2+y^2+z^2}}\hat{x} - \frac{\sigma dydz}{4\pi\epsilon_0(x^2+y^2+z^2)}\frac{y}{\sqrt{x^2+y^2+z^2}}\hat{y}-\frac{\sigma dydz}{4\pi\epsilon_0(x^2+y^2+z^2)}\frac{z}{\sqrt{x^2+y^2+z^2}}\hat{z}.$$Dieses elektrische Feld hat eine Größe, $|d\vec{E}| =\frac{|\sigma |dydz}{4\pi\epsilon_0r^2}$, wobei $r^2 = x^2+y^2+z^2$ und eine Richtung,
$$d\hat{E} = \frac{x}{\sqrt{x^2+y^2+z^2}}\hat{x} - \frac{y}{\sqrt{x^2+y^2+z^2}}\hat{y} -\frac{z}{\sqrt{x^2+y^2+z^2}}\hat{z}.$$Das gesamte elektrische Feld ist die Summe aller Ladungen aus jedem Abschnitt $dydz$.
$$\vec{E} = \int\limits_{-\infty}^{\infty}\int\limits_{-\infty}^{\infty}\frac{\sigma dydz}{4\pi\epsilon_0(x^2+y^2+z^2)}\frac{x}{\sqrt{x^2+y^2+z^2}}\hat{x} - \int\limits_{-\infty}^{\infty}\int\limits_{-\infty}^{\infty}\frac{\sigma dydz}{4\pi\epsilon_0(x^2+y^2+z^2)}\frac{y}{\sqrt{x^2+y^2+z^2}}\hat{y}-\int\limits_{-\infty}^{\infty}\int\limits_{-\infty}^{\infty}\frac{\sigma dydz}{4\pi\epsilon_0(x^2+y^2+z^2)}\frac{z}{\sqrt{x^2+y^2+z^2}}\hat{z}.$$Das zweite Integral verschwindet, wenn die Integration über $y$ durchgeführt wird, weil es eine ungerade Funktion ist, die über ein gerades Intervall ausgewertet wird. In ähnlicher Weise verschwindet das dritte Integral, wenn die Integration über $z$ durchgeführt wird. Das elektrische Feld hat nur eine Komponente senkrecht zur Ladungsebene.
$$\vec{E} = \int\limits_{-\infty}^{\infty}\int\limits_{-\infty}^{\infty}\frac{\sigma dydz}{4\pi\epsilon_0(x^2+y^2+z^2)}\frac{x}{\sqrt{x^2+y^2+z^2}}\hat{x}.$$Unter Verwendung der Identität,
$$\int\limits_{-\infty}^{\infty}\frac{dz}{\left(R^2+z^2\right)^{3/2}} = \frac{2}{R^2},$$wobei $R^2 = x^2 + y^2$,
$$\vec{E} = \int\limits_{-\infty}^{\infty}\frac{x\sigma dy}{2\pi\epsilon_0(x^2+y^2)}\hat{x}.$$Unter Verwendung der Identität,
$$\int\limits_{-\infty}^{\infty}\frac{dy}{\left(x^2+y^2\right)} = \frac{\pi}{|x|},$$Das elektrische Feld ist,
|
$\hspace{0.5cm} \vec{E} = \frac{\sigma}{2\epsilon_0}\text{sgn}(x)\hat{x}.\quad\text{V/m}.\hspace{0.5cm}$ |
$\text{sgn}(x) =1$ für $x > 0$ und $\text{sgn}(x) =-1$ für $x < 0$. Wenn die Flächenladung positiv $(\sigma > 0)$ ist, zeigt das elektrische Feld von der Flächenladung weg in die Richtung senkrecht zur Ebene auf beiden Seiten. Wenn die Flächenladung negativ $(\sigma < 0)$ ist, zeigt das elektrische Feld in Richtung der Flächenladung normal zur Ebene auf beiden Seiten.
Das elektrische Feld, das von einer Ladungsschicht mit beliebiger Ausrichtung erzeugt wird, beträgt:
$$\vec{E}(\vec{r}) = \frac{\sigma}{2\epsilon_0}\text{sgn}((\vec{r}-\vec{r}_0)\cdot\hat {n})\hat{n} \quad\text{V/m},$$wobei $\sigma$ die Ladungsdichte ist, $\hat{n}$ die Normale zur Ebene ist, $\vec{r}_0$ ein Punkt auf der Ebene ist und $\vec{r}$ ist der Punkt, an dem das elektrische Feld beobachtet wird. Bei einer unendlichen Schicht verläuft das elektrische Feld senkrecht zur Ebene, in der die Ladung liegt, und hat eine konstante Stärke, unabhängig davon, wie weit man von der Ebene entfernt ist.
Das entsprechende elektrostatische Potential beträgt:
$$\phi(\vec{r}) = \frac{-\sigma(\vec{r}-\vec{r}_0)\cdot\hat{n}}{2\epsilon_0}\text{ [V ]}.$$