Elektrisches Feld einer linearen Ladungsverteilung

Diese Seite demonstriert das Prinzip der Superposition. Der wichtige Punkt ist, dass, wenn Sie eine Ladungsdichte in Formen zerlegen können, für die die elektrostatischen Potentiale und elektrischen Felder bekannt sind (z. B. Punktladungen und Linienladungen), die elektrostatischen Potentiale und elektrischen Felder addiert werden können, um die Summe zu bestimmen. Dies wird anhand einer Ansammlung von Linienladungen veranschaulicht.

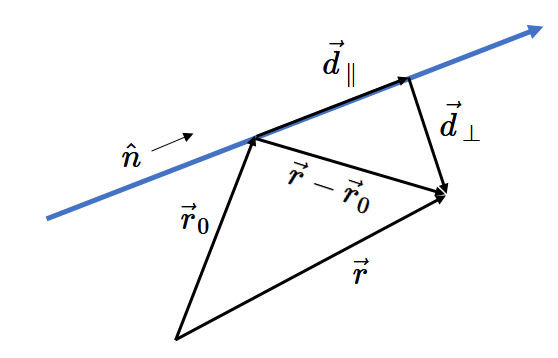
Betrachten Sie eine Ansammlung gleichmäßig geladener langer Stäbe. Die Position der Stab $i$ wird durch Angabe einer Richtung $\hat{n}_i$ angegeben, die durch den Punkt $\vec{r}_i$ geht. Der Vektor, der von $\vec{r}_i$ zu einem anderen Punkt $\vec{r}$ zeigt, ist $\vec{r}-\vec{r}_i$. Dieser Vektor lässt sich in einen Abstand entlang des Stabes und einen Abstand senkrecht zum Stab zerlegen, $\vec{r}-\vec{r}_i = \vec{d}_{\parallel} + \vec{d}_ {\perp}$, wobei die parallele Komponente die Projektion von $\vec{r}-\vec{r}_i$ auf $\hat{n}_i$ ist, $\vec{d}_{\parallel}= \hat{n}_i\cdot(\vec{r}-\vec{r}_i)\,\hat{n}_i$. Die kürzeste Entfernung vom Stab zum Punkt $\vec{r}$ ist $\vec{R}_i = \vec{d}_{\perp}=(\vec{r}-\vec{r}_i)- \vec{d}_{\parallel}$.

Das elektrostatische Potential und das elektrische Feld am Punkt $\vec {r}$ aufgrund einer Ansammlung geladener Stäbchen ist,

wobei $\vec{R}_i = (\vec{r}-\vec{r}_i)-\hat{n}_i\cdot(\vec{r}-\vec{r}_i)\,\hat {n}_i$.

Mit dem untenstehenden Formular können Sie die Ladungsdichten und Positionen von bis zu 10 Stäben angeben und dann das elektrostatische Potential und das elektrische Feld an Position $\vec{r}$ berechnen.