Zwei Punktladungen
Wird das elektrische Feld durch mehrere Punktladungen erzeugt können die Ausdrücke für die elektrischen Felder und das elektrische Potential addiert werden. Für zwei Ladungen ist das elektrische Feld
$$\vec{E}(\vec{r})= \frac{q_1}{4\pi \epsilon_0}\frac{\vec{r}-\vec{r}_1}{ |\vec{r}-\vec{r}_1|^3} + \frac{q_2}{4\pi \epsilon_0}\frac{\vec{r}-\vec{r}_2} {|\vec{r}-\vec{r}_2|^3}\hspace{1cm}\text{[V/m]},$$und das elektrische Potential ist,
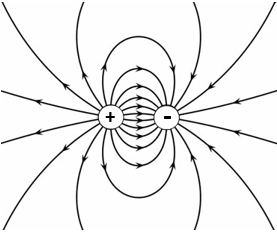
$$\varphi(\vec{r})= \frac{q_1}{4\pi \epsilon_0 |\vec{r}-\vec{r}_1|}+\frac{q_2}{4\pi \epsilon_0 |\vec{r}-\vec{r}_2|}\hspace{1cm}\text{[V]}.$$Im Bild das elektrisches Feldmuster zweier gleicher aber entgegengesetzter Ladungen. Die elektrischen Feldlinien verlaufen immer von der positiven zur negativen Ladung.
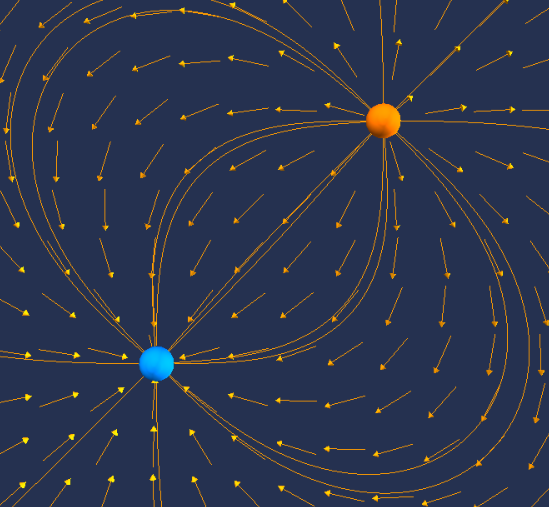
Die Richtung des elektrischen Feldes um zwei Punktladungen wird in der folgenden Abbildung durch die blauen Pfeile dargestellt. Die Ladungen können mit der Maus verschoben werden.
Die Coulomb Kraft und das elektrische Feld sind Vektoren. Die folgende Identität wird benutzt um die einzelnen Komponenten der Vektoren zu berechnen
$$\hat{r}_{2\rightarrow 1} = \frac{\vec{r}_1-\vec{r}_2}{|\vec{r}_1-\vec{r}_2|}= \frac{x_1-x_2}{|\vec{r}_1-\vec{r}_2|}\hat{x}+ \frac{y_1-y_2}{|\vec{r}_1-\vec{r}_2|}\hat{y}+ \frac{z_1-z_2}{|\vec{r}_1-\vec{r}_2|}\hat{z}.$$Die zwischen der Ladung $q_1$ und $q_2$ wirkende (Coulomb) Kraft ist,
$$\vec{F}= \frac{q_1q_2}{4\pi \epsilon_0 |\vec{r}_1-\vec{r}_2|^2}\hat{r}_{2\rightarrow 1} \quad\text{N}.$$Die auf $q_2$ wirkende Kraft ist $-\vec{F}$. Der Vektor $\vec{r}_1-\vec{r}_2$ zeigt von $q_2$ zu $q_1$. Haben $q_2$ und $q_1$ das gleiche Vorzeichen werden beide Ladungen durch die Coulomb Kraft voneinander weggedrückt. Bei unterschiedlichen Vorzeichen der Ladungen werden beiden Ladungen zueinander hingedrückt.
Die Komponenten des Kraftvektors sind,
$$F_x = \frac{q_1q_2(x_1-x_2)}{4\pi \epsilon_0 |\vec{r}_1-\vec{r}_2|^3}\,\,\text{N},\qquad F_y = \frac{q_1q_2(y_1-y_2)}{4\pi \epsilon_0 |\vec{r}_1-\vec{r}_2|^3}\,\,\text{N},\qquad F_z = \frac{q_1q_2(z_1-z_2)}{4\pi \epsilon_0 |\vec{r}_1-\vec{r}_2|^3}\,\,\text{N}.$$|
|