Vorname
Nachname
Matrikelnr.
Problem 1
Ein Ball springt auf den Boden.
$y\,\text{[cm]}$ | |
$x\,\text{[cm]}$ |
Für Zeiten zwischen $t=0$ und $t =$ s, ist der Positionsvektor des Balles,
Was ist die Beschleunigung des Balls zum Zeitpunkt $t=$ s? (Die Position wird in cm angegeben, aber die Beschleunigung sollte in m/s² angegeben werden.)
$\vec{a} = $ $\hat{x} + $ $\hat{y} + $ $\hat{z}$ [m/s²]
Problem 2
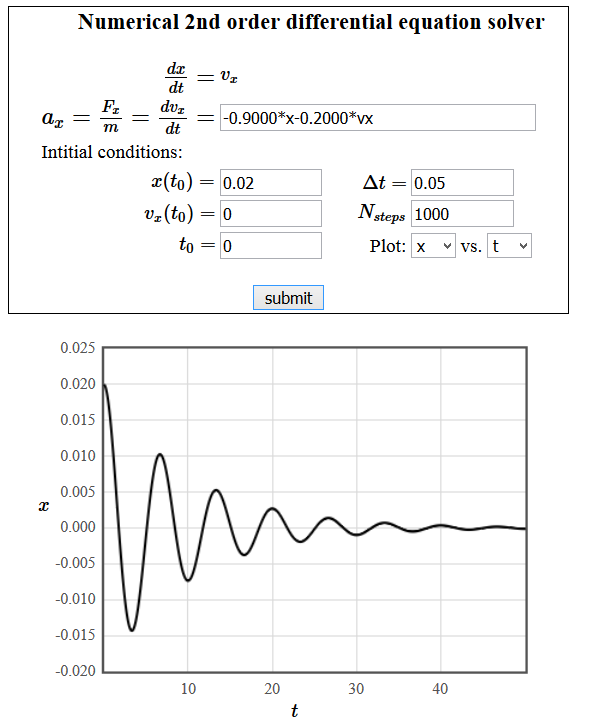
Die Oszillationen eines gedämpften Massenfedersystems wurden mit einem numerischen Differentialgleichungslöser berechnet. Zur Zeit $t=0$ s befand sich eine Masse $m=1$ kg an der um 0.02 m gegenüber der Gleichgewichtsposition ausgelenkten Feder und wurde losgelassen. ImAugenblick des Loslassens hatte die Masse keine Geschwindigkeit.

Aufgrund der Dämpfung wird mechanische Energie in Wärme umgewandelt. Wieviel Energie wurde bis zu dem Zeitpunkt, an welchem die Masse sich nicht mehr bewegt, in Wärme umgewandelt?
$E=$ [J]
Vorname
Nachname
Matrikelnr.
Problem 3
Ein Strom von $I=$ [A] fließt durch ein Z-förmiges Drahtsegment. Das Drahtsegment liegt in der Ebene $z = 0$. Die Stromrichung ist in der Abbildung dargestellt.
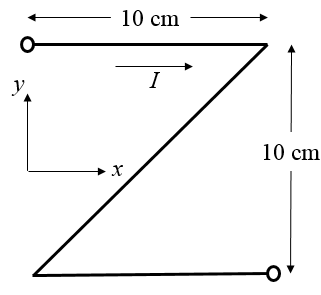
Dieses Drahtsegment befindet sich in einem konstanten magnetischen Feld: