Vorname
Nachname
Matrikelnr.
Problem 1
Die Bahnkurve eines Teilchens der Masse $m=$ g ist,
Dabei ist $t$ die Zeit in Sekunden.
$y$ | |
$x$ |
Welche Kraft wirkt auf das Teilchen zur Zeit $t=$ s?
$\vec{F} = $ $\hat{x} + $ $\hat{y} + $ $\hat{z}$ [N]
Problem 2
Zur Zeit $t=0$ befindet sich ein Elektron an der Position $\vec{r}=0$ und hat die Geschwindigkeit
Die Masse des Elektrons ist $m=9.1094\times10^{-31}\,\text{kg}$ und die Ladung des Elektrons ist $q=-1.6022\times 10^{-19}\,\text{C}$. Das Elektron bewegt sich in einer Region mit einem inhomogenen magnetischen Feld,
\[ \begin{equation} \vec{B}=x\hat{z}\hspace{0.2cm}\text{[T]}. \end{equation} \]Dieses Magnetfeld zeigt in die $z$ Richtung, ist aber abhängig von der Position $x$ in Metern. Welche Differentialgleichung muss gelöst werden, um die Bahnkurve des Elektrons bestimmen zu können?
$ \large \frac{dx}{dt}=$ | $v_x$ | |||
$ \large \frac{dv_x}{dt}=$ | ||||
$ \large \frac{dy}{dt}=$ | $v_y$ | |||
$ \large \frac{dv_y}{dt}=$ | ||||
$ \large \frac{dz}{dt}=$ | $v_z$ | |||
$ \large \frac{dv_z}{dt}=$ | ||||
Wo ist das Elektron bei $t=1$ μs? (Verwenden Sie: Schrittweite $\Delta t = \text{1E-9}$, Anzahl der Schritte $N_{steps}=1000$.)
Problem 3
Ein Gewicht mit der Masse $m=$ kg wird entgegen der Schwerkraft m mit einer konstanten Geschwindigkeit $v=$ m/s bewegt. Die Anfangsposition des Gewichts ist $\vec{r}=0$ und die Endposition ist $\vec{r}=$ $\hat{z}$ [m]. Es wirkt eine Reibungskraft $\vec{F}_{drag}=-|\vec{v}|\vec{v}$ N. Die nach unten gerichtete Gravitationskraft und die Reibungskräfte sind,
\[ \begin{equation} \vec{F}=-mg\hat{z}-|\vec{v}|\vec{v}\hspace{0.2cm}\text{[N]}. \end{equation} \]Wie viel Arbeit wird beim Heben des Gewichts verrichtet?
$W=$ [J]
Die Gravitationsbeschleunigung auf der Erdoberfläche ist $g=9.81$ m/s².
Problem 4
Das die Ladungsdichte einer linearen Diode hat die Form
in der Umgebung - μm < $x$ < μm. $x$ wird hier in Metern gemessen. Wie lautet das elektrische Feld in dieser Umgebung?
Die relative dielektrische Konstante von Silizium ist $\epsilon_r=12$. Die elektrische Feldkonstante ist $\epsilon_0=8.85\times 10^{-12}$ F/m.
Problem 5
Zweidimensionale Wellen werden von zwei punktförmigen Quellen, die sich an $\vec{r}_1=-2\hat{x}$ [m] und $\vec{r}_2=2\hat{x}$ [m] befinden ausgesendet. Das resultierende Interferenzmuster wird beschrieben durch,
Hier werden $z$ und $r$ in Metern und $t$ in Sekunden angegeben.
Wie groß ist die Wellenlänge der Wellen?
$\lambda=$ [m]
Wie lautet die Winkelfrequenz der Wellen?
$\omega=$ [rad/s]
Wie lautet die Wellengeschwindigkeit?
$v=$ [m/s]
Wann gibt es destruktive Interferenz $(z=0)$ an der Stelle $\vec{r}=0$?
$t=$ [s] (Es gibt mehrere Lösungen. Geben Sie eine davon.)
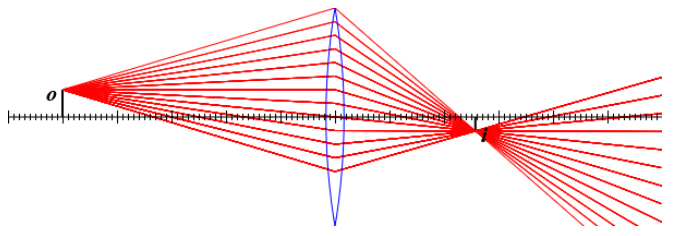
Problem 6

Wie groß ist die Brennweite dieser Linse (in cm, gerundet auf die erste Nachkommastelle)? Die kleine Teilung des Ma▀stabes ist in mm.