Exercise questions 7: Phonons

The propagation of low frequency (long wavelength) sound and the propagation of light in vacuum can both be described by the wave equation. Since the same classical equation describes both cases, the calculation of the quantum states and the thermodynamic properites for sound is very similar to that for light. The quantized particles of sound are called phonons. The differences between photons and phonons are that phonons travel at the speed of sound instead of the speed of light and there is one more possible polarization for sound waves than for light waves. Sound waves can have a polarized along the direction of propagation (longitudinal polarization) and there are two possible transverse polarizations. This makes the density of modes for phonons a factor of 3/2 greater than the density of modes for photons.

7.1 (a) At low temperatures, only the low energy (= long wavelength) modes are occupied. In the low temperature limit, what is the equivalent of Planck's radiation law for phonons?

(b) What is the specific heat of the phonons in the low temperature limit?

7.x In aluminum, the longitudinal sound velocity is $c_l=6.32\times 10^3$ m/s and the transverse sound velocity is $c_t=3.1\times 10^3$ m/s. The sound velocity is the slope of the phonon dispersion relation $(\omega \text{ vs. }k)$ near $k=0$.

(a) Determine the density of states for the transverse and longitudinal modes in the long wavelength limit. There are 2 polarizations of the transverse modes and one polarization of the longitudinal mode. Add these densities of states together to get the total density of states.

(b) From the density of states, determine the low temperature form of the phonon contribution to the specific heat of aluminum. It may be useful to know that,

$$\int_0 ^\infty \frac{x^3}{e^x - 1} \mathrm{d}x = \frac{\pi^4}{15}.$$

7.2 A crystal has a volume of 1 cm³ and a sound velocity of 6000 m/s. At $T$ = 300 K, what is the number of phonons between the frequencies 4.0 × 10⁶ Hz and 4.1 × 10⁶ Hz? (Hint: 4.0 × 10⁶ Hz is much lower than the Debye frequency so the dispersion relation is linear at these freqeuncies and the crystal structure is not relevant. This is the long-wavelength limit. First calculate the number of phonon modes in this frequency interval. Then use the Bose-Einstein factor to calculate the mean number of phonons in these modes.)

7.3 The speed of sound in copper is 3560 m/s. The crystal structure is fcc and the lattice constant (of the conventional unit cell) is $a=361.5$ pm. The point farthest from Γ on the first Brillouin zone boundary is the symmetry point W where $\overline{\Gamma W}=\sqrt{5}\pi/a$. Estimate the Debye frequency from this information.

When we are not in the low temperature limit, the phonon modes have to be calculated and then the occupation of the phonon modes can be determined using the Bose-Einstein function. To determine the phonon modes, a crystal is described as a mass-spring system where the masses are the atomic masses and the springs are the effective spring constants of the bonds between the atoms. The motion of the atoms can be described in terms of the normal modes. In a normal mode, all of the atoms move with the same frequency. Because of the translational symmetry we can show that the normal mode of a crystal with one atom per Bravais lattice point has the form,

\[ \begin{equation} \vec{u}_{lmn} = \vec{u}_{\vec{k}}\exp\left(i\left(l\vec{k}\cdot\vec{a}_1+m\vec{k}\cdot\vec{a}_2+n\vec{k}\cdot\vec{a}_3-\omega t\right)\right). \end{equation} \]

Here $l$, $m$, and $n$ are integers, $\vec{a}_1,\,\vec{a}_2,$ and $\vec{a}_3$ are the primitive lattice vectors in real space, $\vec{k}$ is a wave vector that labels a phonon mode, and $\vec{u}_{lmn}$ is the displacement vector of atom $lmn$ from its equilibrium position. The $x$-component of $\vec{u}_{lmn}$ is the displacement from equilibrium in the $x$-direction, etc.

There are $3N$ degrees of freedom in a crystal consisting of $N$ atoms. There is a degree of freedom for the $x-$, $y-$, and $z-$motion of every atom. Therefore, the motion of the atoms can be described by $3N$ normal modes. For every $\vec{k}$ vector, there are $3p$ modes: three acoustic modes and $3p-3$ optical modes. Here $p$ is the number of atoms in the basis. Since $N=pN_{uc}$, where $N_{uc}$ is the number of primitive unit cells in the crystal, $3N = 3pN_{uc} = 3pN_{\vec{k}}$, where $N_{\vec{k}}$ is the number of allowed $\vec{k}$ vectors. The number of allowed $\vec{k}$ vectors equals the number of primitive unit cells in the crystal.

7.x Show that the phonon eigenfunctions are also eigenfunctions of the translation operator. What are these eigen functions for a hexagonal close packed lattice? Give the eigenfunctions in Cartesian coordinates $(x, y, z)$.

7.4 For a linear chain with equivalent masses connected by equivalent springs, the mass-spring system is described by the equation,

\[ \begin{equation} M\frac{d^2u_{l}}{dt^2} = C(u_{l+1}-u_l)-C(u_{l}-u_{l-1}). \end{equation} \]

Here $C$ is the effective spring constant of the bonds. Show that by substituting the general form for the normal mode solutions into this equation, the dispersion relation for a linear chain can be determined.

When there are more atoms in the basis, the phonon normal modes are described by a displacement vector for every atom in the basis. For two atoms in the basis, the displacement vectors are,

\[ \begin{equation} \vec{u}_{lmn} = \vec{u}_{\vec{k}}\exp\left(i\left(l\vec{k}\cdot\vec{a}_1+m\vec{k}\cdot\vec{a}_2+n\vec{k}\cdot\vec{a}_3-\omega t\right)\right), \end{equation} \] \[ \begin{equation} \vec{v}_{lmn} = \vec{v}_{\vec{k}}\exp\left(i\left(l\vec{k}\cdot\vec{a}_1+m\vec{k}\cdot\vec{a}_2+n\vec{k}\cdot\vec{a}_3-\omega t\right)\right). \end{equation} \]

7.x Consider a linear chain of equilavent masses but alternating spring constants $C_1$ and $C_2$. What are the equations of motion that describe this system? Show that by substituting the general form for the normal mode solutions into this equation, the dispersion relation can be determined.

7.x (a) If only linear springs connecting nearest neighbors are included, what are the equations that describe the phonon modes of a CsCl crystal? Let $\vec{u}_{lmn}$ describe the motion of the Cs atom at site $lmn$ and $\vec{v}_{lmn}$ describe the motion of the Cl atom at site $lmn$.

(b) By substituting the normal mode solutions into the equations of motion, determine the dispersion relation. The dispersion relation in this case is a set of 6 equations with 6 unknowns.

7.x Why does the phonon dispersion relation for silver look like the phonon dispersion relation for gold?

To sketch approximately the phonon dispersion for a crystal, first consider the reciprocal lattice of the Bravais lattice of that crystal. Label horizontal axis with symmetry points of the reciprocal lattice. Take care that the spacing between those symmetry points equals the distance between the symmetry points in reciprocal space. There are 3 acoustic branches of the phonon dispersion relation that start linearly at $\Gamma$. The slope of the dispersion curve near $\Gamma$ is the speed of sound. There is a longitudinal acoustic branch and two transverse acoustic branches. Typically, the longitudinal mode at a specific $\vec{k}$ vector has a higher frequency than the transverse modes. The transverse modes will have the same frequency if the crystal has a symmetry that maps one transverse mode onto the other. For instance, the transverse modes propagating in the <100> directions of a cubic crystal are degenerate. The dispersion curves will bend and strike the Brillouin zone boundaries at 90°. For $p$ atoms in the basis, there will be $3p-3$ optical branches. These have higher frequencies than the acoustic branches and strike the Brillouin zone boundaries at 90°.

7.5 Sketch the phonon dispersion relation for SrTiO₃ (simple cubic), NaCl (fcc), and Cr (bcc).

7.x Diamond has an fcc Bravais lattice. The primitive lattice vectors are,

$\vec{a}_1=\frac{a}{2}\hat{x}+\frac{a}{2}\hat{y}$, $\vec{a}_2=\frac{a}{2}\hat{x}+\frac{a}{2}\hat{z}$, $\vec{a}_3=\frac{a}{2}\hat{y}+\frac{a}{2}\hat{z}$.

There are two atoms in the basis. The positions of the two carbon atoms given in terms of the fractional coordinates of the conventional unit are,

$\vec{B}_1=(0,0,0)$, $\vec{B}_2=(0.25,0.25,0.25)$.

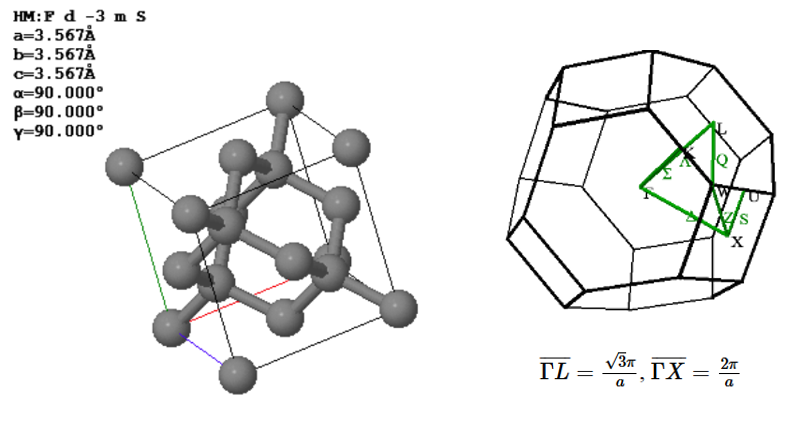
(a) How many $\vec{k}$ vectors satisfy periodic boundary conditions for a diamond crystal 1 cm³ (The lattice constant is $a=3.567$ Å.)

(b) The lattice vibrations can be described in terms of normal modes. How many normal modes does a diamond crystal 1 cm³ have?

7.x An fcc crystal has two atoms per unit cell. Sketch the phonon dispersion relation (frequency vs. wavenumber). On the wavenumber axis, indicate the positions of Γ, X, and L.

7.6 Below is the phonon dispersion relation for a crystal with an fcc structure. The lattice constant is a = 0.2 nm.

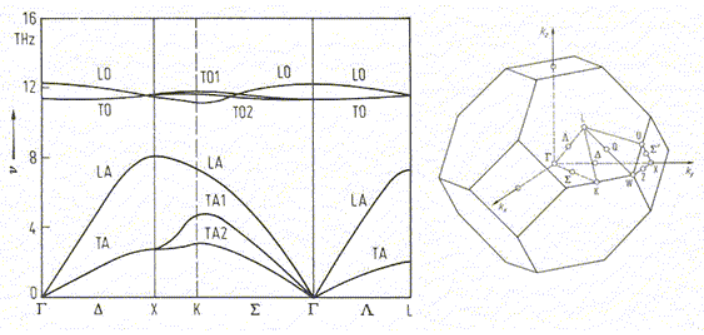
(a) How many atoms are there in the primitive unit cell?

(b) Choose a direction and a polarization (longitudinal or transverse) and estimate the speed of sound in this direction for long wavelength sound waves.

(d) Which of these phonon states would be more than 40% occupied at 300 K?

Hint: Note that the dispersion plot uses ν in THz (instead of ω)

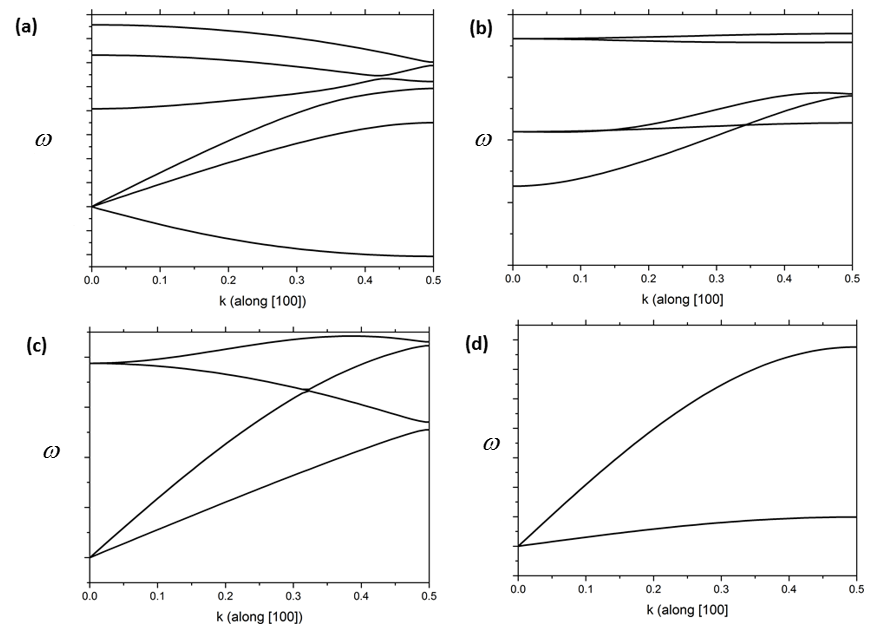
7.x CsI has a simple cubic Bravais lattice with a Cs atom at (0,0,0) and an I atom at (0.5 0.5 0.5). Which of the figures below is the phonon dispersion curve for CsI? Explain your reasoning.

The phonon density of states can be calculated numerically from the phonon dispersion relation by considering every $\vec{k}$-point in the first Brillouin zone and recording how often a frequency $\omega$ appears.

7.x A crystal has two atoms in the basis and there is a band gap in the density of states between the acoustic branches and the optical branches. (For example GaN). What is the ratio of the integral of the density of states over all acoustic states divided by the integral of the density of states over all of the optical states?

7.x Calculate the density of gold from the phonon density of states. By numerically integrating over all frequencies it is possible to determine the number of phonon modes per m³. This must be equal to number of vibrational degrees of freedom per m³. The number of vibrational degrees of freedom is 3 times the number of atoms per m³. Calculate the concentration of atoms per m³ and multiply by the mass of an atom to get the density.

Many thermodynamic properties can be calculated from the density of states. Since phonons are bosons, the formula's are:

Internal energy density:	\begin{equation} u = \int \limits_{0}^{\infty} \frac{\hbar\omega D(\omega)}{\exp\left( \frac{\hbar\omega}{k_BT} \right)-1}d\omega \end{equation}
Specific heat:	\begin{equation}c_v=\frac{\partial u}{\partial T}=\int \limits_{0}^{\infty}\frac{\hbar^2\omega^2 D(\omega)\exp\left(\frac{\hbar\omega}{k_BT}\right)}{k_BT^2\left[\exp\left(\frac{\hbar\omega}{k_BT}\right)-1\right]^2}d\omega \end{equation}
Entropy density:	\begin{equation} s = \int \frac{c_v}{T}dT =-k_B \int \limits_{0}^{\infty}D(\omega)\left( \ln \left[ 1-\exp\left( \frac{-\hbar\omega}{k_BT} \right) \right]+\frac{\hbar\omega}{k_BT\left(1-\exp\left( \frac{\hbar\omega}{k_BT} \right)\right) } \right) d\omega \end{equation}
Helmholz free energy density:	\begin{equation} f=u-Ts= \int \limits_{0}^{\infty} D(\omega) \left( k_BT\ln\left[ 1-\exp\left( \frac{-\hbar\omega}{k_BT} \right)\right] \right) dE \end{equation}

7.x Calculate the specific heat and the derivative of the specific heat with respect to temperature $dc_v/dT$ of silicon at 300 K. Use this table of the phonon density of states and this program to calculate the specific heat.

7.x The phonon dispersion relation of GaN is shown below.

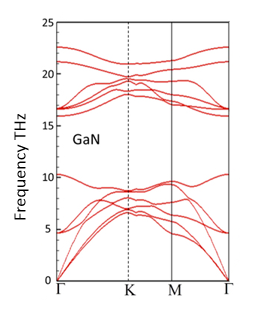
(a) How many atoms are there in the basis of GaN?

(b) How does symmetry help find the form of the normal modes? Write down the formula for the normal modes.

Below is the phonon density of states of GaN.

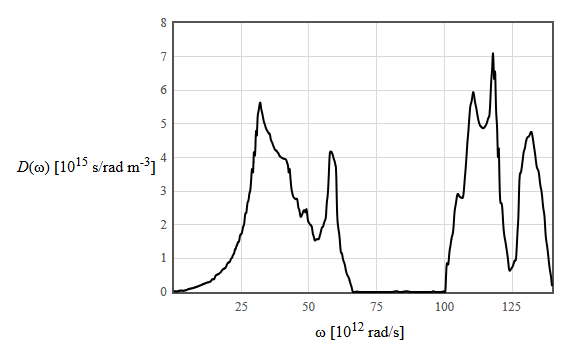
(d) What is the density of occupied phonon states in a frequency interval $\Delta \omega=10^4$ [rad/s] centered at an angular frequency of $50 \times 10^{12}$ rad/s at 300 K?