PHY.K02UF Molecular and Solid State Physics
|
| ||||
PHY.K02UF Molecular and Solid State Physics | ||||
When electrons move through a crystal, the allowed electron energies are arranged in bands. Electron states in a band have wave functions that extend over the whole crystal. Electrons states with energies not in a band are in a band gap. The wave functions for electron states in a band gap decay exponentially from the edge of the sample. The current density associated with an electron wavefunction $\psi$ is proportional to $\psi^* \nabla\psi-\psi \nabla \psi^*$ and is uniform for states in a band while it is zero for states in a band gap.
9.x The wave functions for electrons moving in any one-dimensional crystal can be calculated numerically. Using the program to solve the Schrödinger equation for 1-D potentials, sketch the form of the wave function for an energy in a band and an energy in a band gap. Use the potential $\cos (\pi x)$ where $x$ is measured in Ånstroms. Energies $8.9 < E < 9.89$ eV are in a band gap for this potential. What is the velocity associated with the two states you have sketched?
The symmetry of the crystal requires that the electron eigen states are also eigen functions of the translation operator. It can be shown that the wave functions in a band must have Bloch form, $\psi(\vec{r}) = e^{i\vec{k}\cdot\vec{r}}u_\vec{k}(\vec{r})$, where $\vec{k}$ is a reciprocal lattice vector and $u_\vec{k}(\vec{r})$ is a periodic function with the periodicity of the crystal.
9.1 (a) Show that $\psi(\vec{r}) = e^{i\vec{k}\cdot\vec{r}}u_\vec{k}(\vec{r})$ is an eigen function of the translation operator $\textbf{T} = l\vec{a}_1+m\vec{a}_2+n\vec{a}_3$ and determine the eigenvalue. Here $l$, $m$, and $n$ are integers and $\vec{a}_1$, $\vec{a}_2$, and $\vec{a}_3$ are the primitive lattice vectors.
(b) Consider a crystal with dimensions $N_1\vec{a}_1\times N_2\vec{a}_2\times N_3\vec{a}_3$. The number of unit cells is $N=N_1N_2N_3$. The wave functions that satisfy periodic boundary conditions have an integer number of wavelengths in the directions of $\vec{a}_1$, $\vec{a}_2$, and $\vec{a}_3$. Show that if $\vec{k}=u\vec{b}_1+v\vec{b}_2+w\vec{b}_3$ is a reciprocal lattice vector in the first Brillouin zone, a solution of Bloch form satisfies periodic boundary conditions. A useful identify is, $\vec{a}_i\cdot\vec{b}_j=2\pi\delta_{ij}$.
For a crystal with $N$ primitive unit cells, there are $N$ translational symmetries that map one primitive unit cell onto another if periodic boundary conditions are applied. There are also $N$ reciprocal lattice vectors in the first Brillouin zone. Every reciprocal lattice vector corresponds to one Bloch solution. Thus, there are $N$ electron states per band. Because of spin, each electron state can be occupied by two electrons. There are $2N$ electrons per band.
9.x Using the program to calculate the dispersion relation for a 1-D potential, sketch the dispersion relations and the density of states for the potentials $V(x) = 0.1\cos (\pi x)$, $V(x) = 3\cos (\pi x)$, and $V(x) = 10\cos (\pi x)$, where $x$ is measured in Ånstroms. You may have to reduce the energy $E_1$ in the program to see the whole dispersion curve. In the limit that the amplitude of the potential goes to zero, the dispersion relation approaches that of the free electron model. As soon as there is a finite potential, the dispersion relation separates into bands and band gaps. The density of states is zero in the bandgaps and diverges at the band edges (Van Hove singularities). Every band contains 2$N$ electrons states where $N$ is the number of unit cells in the crystal.
9.x An electron experiences a 1-D periodic potential, $V(x)=10 H(x-a/2)$ for $0 < x < a$. $H(x)$ is the Heaviside function. The lattice constant is $a=1.5$ Å. The lowest band is half filled. What is the electronic contribution to the specific heat at 300 K? This problem should be solved by first calculating the electron density of states numerically and then using the density of states to calculate the specific heat numerically. Use the Kronig Penney model to calculate the density of states because in that case there is an analytic formula for the density of states and there are fewer numerical problems with the van Hove singularities. Compare the result you get to the free electron model.
For weak periodic potentials in 2-D and 3-D, the dispersion relation is also almost the same as for the free electron model. The empty lattice approximation can be used to construct the dispersion in this case. Draw a parabola of the form $E+\hbar^2|\vec{k}-\vec{G}|/2m$ at every reciprocal lattice point $\vec{G}$. Make cuts through this family of parabolas in the high symmetry directions to plot the dispersion relation in those directions. An example for simple cubic is shown below.
Elastic scattering of electron waves at the Brillouin zone boundaries satisfies the diffraction condition $\Delta\vec{k}=\vec{G}$. This causes the electron dispersion relation $E$ vs. $\vec{k}$ to bend and strike the Brillouin boundaries at 90°.
9.2 Draw the electron dispersion relation along L-Γ-X for aluminum (an fcc metal). Start with the empty lattice approximation and explain how this should be modified to include periodic potential that the electron experiences. For fcc, $\overline{\Gamma L}= \frac{\sqrt{3}\pi}{a}$ and $\overline{\Gamma X}= \frac{2\pi}{a}$.
9.x A metal with a simple cubic Bravais lattice has one valence electron per unit cell. How large is the Fermi wave vector $k_F$ compared to $|\vec{k}|$ at the symmetry point $\text{R}$ at the corner of the Brillouin zone?
A material with a partially filled band is a metal. Sometimes the bands overlap in energy so there are more partially occupied bands. If all bands are completely filled and there is a band gap between the highest occupied band and the lowest unoccupied band, the material is a semiconductor or an insulator. A semiconductor has a band gap $E_g < 3$ eV while an insulator has a band gap $E_g > 3$ eV.
9.3 The density of states for a particular material is given in the following figure. The total electron density is 9 × 1028 electrons/m³. The form of the density of states was chosen to make it easy to integrate (by counting squares).
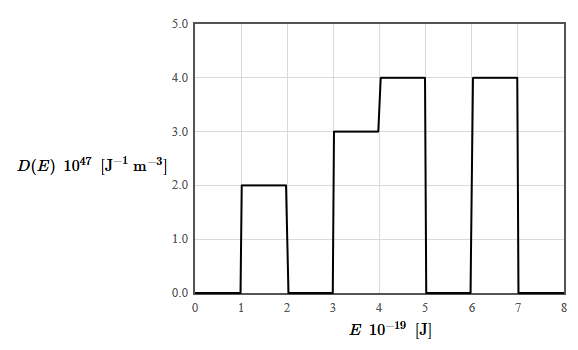
(a) Is this material a metal, an insulator, or a semiconductor? Why?
(b) What is the limiting value of the Fermi energy as the temperature approaches zero?
9.x A semiconductor has a band gap of 1 eV. The chemical potential lies in the middle of the band gap. What is the value of the Fermi function at the valence band edge and at the conduction band edge at a temperature of 300 K?
Tight binding is a method to calculate the electronic band structure of a crystal. It is similar to the method of Linear Combination of Atomic Orbitals (LCAO) used to construct molecular orbitals. The tight-binding wavefunction is,
\begin{equation} \psi_{\vec{k}}\left(\vec{r}\right)=\frac{1}{\sqrt{N}}\sum\limits_{h,j,l}e^{i\left(h\vec{k}\cdot\vec{a}_1 + j\vec{k}\cdot\vec{a}_2 + l\vec{k}\cdot\vec{a}_3\right)} \psi_{\text{unit cell}}\left(\vec{r}-h\vec{a}_1-j\vec{a}_2-l\vec{a}_3\right). \end{equation} Here $N$ is the number of unit cells in the crystal; $h$, $j$, and $l$ are integers that are used to label all the unit cells in the crystal; $\vec{k}$ is a wave vector; $\vec{a}_1$, $\vec{a}_2$, and $\vec{a}_3$ are primitive lattice vectors in real space, and $\psi_{\text{unit cell}}(\vec{r})$ is a trial wavefunction that is constructed from the valence orbitals $\phi_{i}$ of all of the atoms in a primitive unit cell, \begin{equation} \psi_{\text{unit cell}}\left(\vec{r}\right)=\sum\limits_{i}c_{i}\phi_{i}\left(\vec{r}-\vec{r}_i\right). \end{equation}Here $c_{i}$ are coefficients that are determined by substituting the wave function into the Schrödinger equation and $\vec{r}_i$ is the position of the nucleus for the $i$th orbital.
9.x Calculate the electron dispersion relation for an hexagonal crystal in the tight binding approximation. Use one valence orbital per unit cell. This will result in one band. Assume there is with one atom per unit cell and $c = a$.
Another way to calculate the bandstructure of a material is the plane wave method. We start with the same Schrödinger equation as for the tight-binding model,
\begin{equation} \frac{-\hbar^2}{2m}\nabla^2\psi(\vec{r})+V(\vec{r})\psi(\vec{r})=E\psi(\vec{r}). \end{equation}In the plane wave method, the potential and the wave function are expressed as Fourier series,
\begin{equation} V(\vec{r})=\sum\limits_{\vec{G}}V_{\vec{G}}e^{i\vec{G}\cdot\vec{r}},\hspace{1.5cm}\psi(\vec{r})=\sum\limits_{\vec{k}}C_{\vec{k}}e^{i\vec{k}\cdot\vec{r}}. \end{equation}These expressions are substituted into the Schrödinger equation and terms with the same wavelength are collected together. This results in the central equations,
\begin{equation} \left(\frac{\hbar^2k^2}{2m}-E\right)C_{\vec{k}}+\sum\limits_{\vec{G}}V_{\vec{G}}C_{\vec{k}-\vec{G}}=0. \end{equation}These equations are solved for every $\vec{k}$ vector in the first Brillouin zone.
9.x Consider 1-D periodic potential, $V(x)=\cos(\pi x)$ where $x$ is measured in Ånstroms. There are only two terms in the Fourier series for the potential $\cos(\pi x)=(e^{i\pi x}+e^{-i\pi x})/2$.
(a) Write down the central equations in matrix form.
(b) Truncate the matrix to a 3 × 3 matrix and solve for the 3 energies at $k=0$ and $k=\frac{\pi}{a}$ where $a=2$ Å.
There are other more exact methods to calculate the band structure of a material such as density functional theory or the Hartree-Fock method. In these methods the Schrödinger equation is solved and some approximation is used to include the electron-electron interactions. The results of these calculations can be found in the scientific literature. The electron density of states can be calculated numerically by choosing uniformly distributed $\vec{k}$ vectors in the first Brillouin zone and calculating the allowed energies using the dispersion relation. The density of states is proportional to the histogram of the energies that occur. Using the density of states, the thermodynamic properties can be calculated numerically.
Chemical potential: | \begin{equation} n = \int_{-\infty}^{\infty}D(E)f(E)dE. \end{equation} | |
| ||
| ||
Internal energy density: | \[ \begin{equation} u= \int_{-\infty}^{\infty}\frac{ED(E)}{\exp\left(\frac{E-\mu}{k_BT}\right)+1}. \end{equation} \] | |
| ||
Specific heat: | \[ \begin{equation} c_v=\frac{du}{dT}= \int_{-\infty}^{\infty}\frac{ED(E)(E-\mu)\exp\left(\frac{E-\mu}{k_BT}\right)}{k_BT^2\left(\exp\left(\frac{E-\mu}{k_BT}\right)+1\right)^2}dE. \end{equation} \] | |
Entropy density: | \begin{equation} s=\int \frac{c_v}{T}dT=\frac{1}{T}\int\limits_{-\infty}^{\infty}D(E)\left[\frac{E-\mu}{1+\exp\left(\frac{E-\mu}{k_BT}\right)}+k_BT\ln\left(\exp\left(-\frac{E-\mu}{k_BT}\right)+1\right)\right]dE \end{equation} | |
| ||
Helmholz free energy density: | \[ \begin{equation} f=u -Ts= \int_{-\infty}^{\infty}D(E)\left(\frac{\mu}{\exp\left(\frac{E-\mu}{k_BT}\right)+1}- k_BT\ln\left(\exp\left(-\frac{E-\mu}{k_BT}\right)+1 \right)\right)dE. \end{equation} \] | |
|
Some examples of calculated electronic density of states are: Al fcc, Au fcc, Cu fcc, Li bcc, Na bcc, Pt fcc, W bcc, Si diamond, Fe bcc, Ni fcc, Co fcc, Mn bcc, Cr bcc, Gd hcp, Pd fcc, Pd3Cr, Pd3Mn, PdCr, PdMn, GaN, 6H SiC, GaAs, GaP, Ge, InAs.
9.x Use the electron density of states of copper to calculate the electronic contribution to the specific heat of copper at 300 K.
9.4 Aluminum has a electrical resistivity of $\rho= 2.7\,\mu\Omega\text{ cm}$ and a Hall constant $R_H = -3.5 × 10^{-11}\text{ m}^3/\text{C}$ at room temperature. Calculate the density of valence electrons $n$, the electron mobility $\mu$, and the scattering time $\tau_{sc}$.
9.x Copper has an electrical conductivity of 5.96 × 107 S/m. Estimate the thermal conductivity of copper.
9.x What experimental techniques can be used to measure the electron density of states?
9.x (a) Using the empty lattice approximation, draw the electronic band structure of a bcc metal.

(b) This metal has one valence electron per unit cell. Include the Fermi energy in your drawing.
(c) $E=0$ is indicated in the plot. What is approximately the Fermi energy in electron volts if the lattice constant is $a=4.3$ Å? (You can estimate $E_F$ if you calculate the energies where the dispersion curve meets the Brillouin zone boundaries.)
9.x The density of states for a particular material is given in the following figure. The total electron density is $14 \times 10^{28}$ electrons/m³. The form of the density of states was chosen to make it easy to integrate (by counting squares).
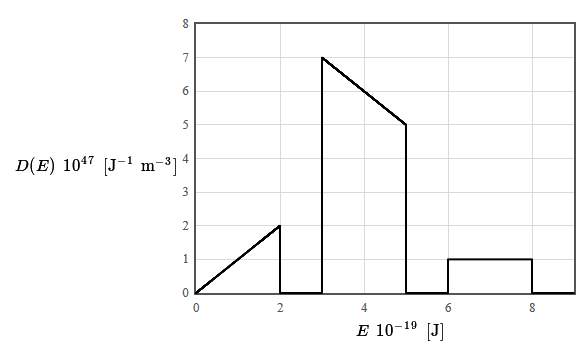
(a) Is this material a metal, an insulator, or a semiconductor? Why?
(b) What is the limiting value of the Fermi energy as the temperature approaches zero?