PHY.K02 Solid State Physics
27.06.2024

Name Matrikelnr.

Each subsections (a), (b), (c), $\cdots$ can be awarded a maximum of 5 points.

(a) The many particle Hamiltonian below is incomplete. All of the signs are missing and the Coulomb terms are not complete. $$H_{\text{mp}}= \quad\sum\limits_i \frac{\hbar^2}{2m_e}\nabla^2_i \quad\sum\limits_a \frac{\hbar^2}{2m_a}\nabla^2_a \quad\sum\limits_{a,i} \frac{ }{4\pi\epsilon_0 |\vec{r}_i-\vec{r}_a|}\quad\sum\limits_{i< j} \frac{}{4\pi\epsilon_0 |\vec{r}_i-\vec{r}_j|}\quad\sum\limits_{a< b} \frac{ }{4\pi\epsilon_0 |\vec{r}_a-\vec{r}_b|} .$$

Here $i$ sums over the electrons and $a$ sums over the atoms. Add $+/-$ signs where appropriate and complete the Coulomb terms.

(b) Write the Molecular orbital Hamiltonian for a He₂ molecule.

(c) The bond potential for He₂ is shown below. Circle the point on the bond potential where the force between the He atoms is the greatest.

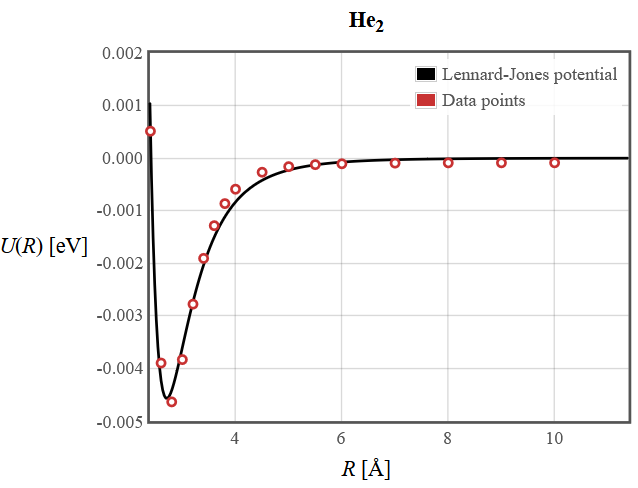
(d) Explain why the bond in He₂ is particularly weak.

(e) Express the rotational energy levels of He₂ in terms of the mass of an He atom $m_{\text{He}}$ and the equilibrium bond length $r_0$. How many rotational degrees of freedom are there?

Problem 2

Consider an electron in the periodic potential,

$$U(\vec{r})=\cos (x) + \cos (y) +\cos (z)\qquad \text{eV}.$$

The distances are given in Ångstroms.

(a) What is the Bravais lattice?

(b) What are the reciprocal lattice vectors of this potential? Don't forget the units.

(c) The intensity of a diffraction peak is proportional to the square of the Fourier coefficient of that reciprocal lattice vector. How many nonzero diffraction peaks would be observed for this potential?

(d) Give two elements of the point group of this crystal as matrices.

(e) Sketch the $E$ vs. $k$ electron dispersion relation for this potential. There is a bandgap at the Brillouin zone boundary. How can you estimate the size of this bandgap?

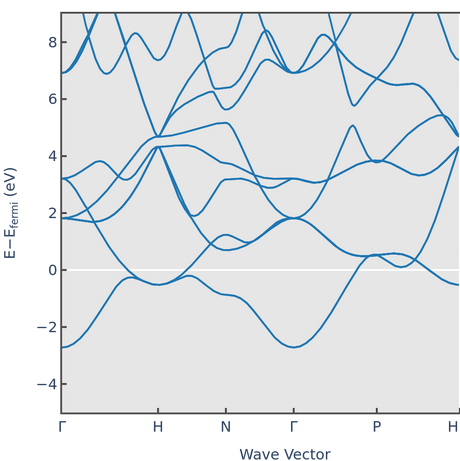
Problem 3

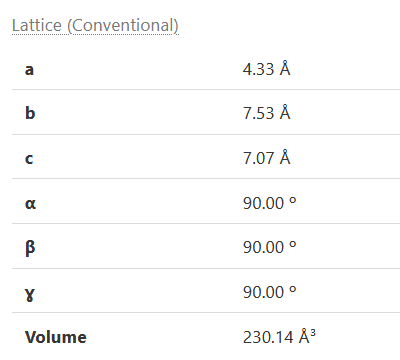
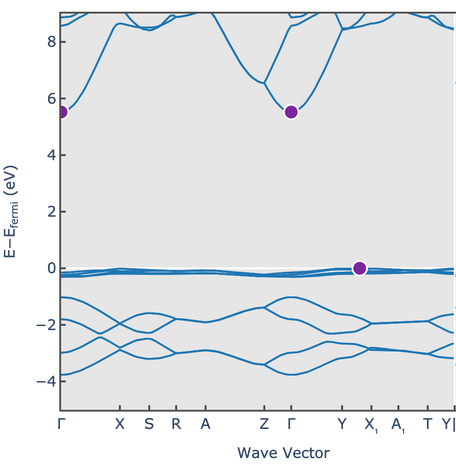
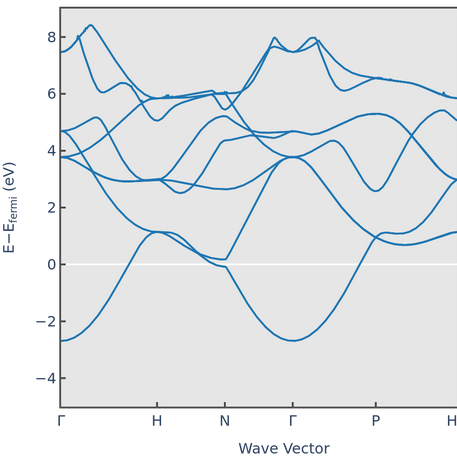
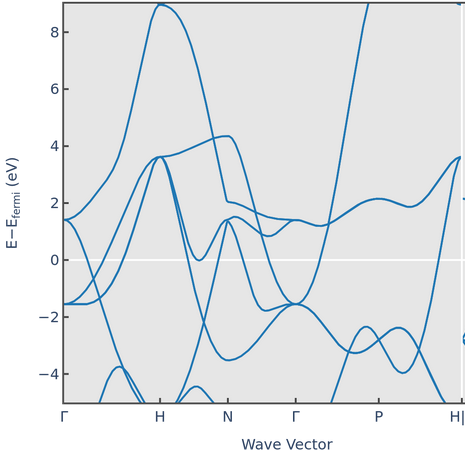
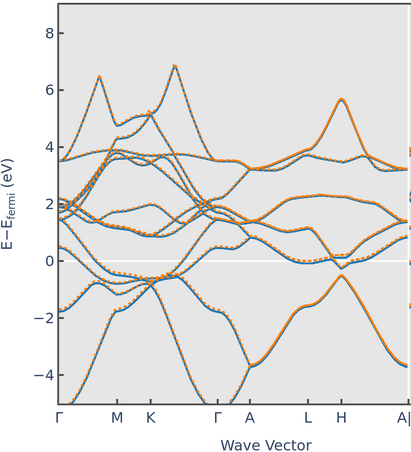
Water ice can crystalize in many crystal structures. The lattice constants and electron dispersion relation for one of the structures is shown below.

(a) What is the Bravais lattice?

(b) Is this phase of ice a metal, a semiconductor, or an insulator? Explain your reasoning.

(d) In the tight-binding model, the flat bands near the Fermi energy come from bands formed by the oxygen atomic orbitals. Why are these bands particularly flat?

(e) To determine the temperature at which a phase transition will occur to another phase, you would have to calculate the electron contribution and the phonon contribution to the free energy. Which contribution would dominate for ice? Explain your reasoning.

Problem 4

(a) The free electron model depends on two parameters, the electron density $n$ and the effective mass $m^*$. How could these parameters be determined experimentally?

(b) Match the Fermi surface to the bandstructure. (Draw a line between the matching pairs.)

$$\psi_{k}(x) = e^{ikx}u_{k}(x)$$

where $k$ is in the 2nd Brillouin zone. The Brillouin zone boundary is at $\frac{\pi}{a}$ where $a$ is the lattice constant. This can be rewritten as $\psi_{k'}(x) = e^{ik'x}u_{k'}(x)$ where $k'$ is in the first Brillouin zone. What is $u_{k'}(x)$ in terms of $u_k(x)$ and $a$?

(d) Why is the electric susceptibility considered a symmetric matrix?

(e) The piezoconductivity describes how the electrical conductivity changes as the stress on the crystal changes. What rank tensor is the piezoconductivity?

Solution

(a) The free electron model depends on the valence electron density $n$ (not the total electron density) and the effective mass $m^*$.

A direct way to measure $n$ is a Hall effect measurement and a direct way to measure $m^*$ would be cyclotron resonance.

A photoemission could confirm that the density of states follows a $\sqrt{E}$ dependence. The form of the square root would could be used to calcuate the effective mass and the total area would be the electron density.

An ARPES measurement would measure the band structure near the Fermi energy and from that you could extract the effective mass.

All of the thermodynamic properties depend on $n$ and $m^*$. Two thermodynamic properties that you can measure are the specific heat and the bulk modulus. It would be necessary to separate the electron contribution from the phonon contribution. This can be done for the specific heat by measuring at low temperatures and fitting to $c_v = \gamma T + AT^3$. The $\gamma$ factor describes the electron contribution and this can be used to estimate the effective mass.

(b)

<table align="center"><tr>
<td style="border: 1px black solid";><img src="K.png" height = "100" /> The Fermi surface is spherical indicating that it is not close to the Brillouin zone boundaries. This would be the case for a metal with one valence electron. For one valence electeron, the lowest band would be half filled. <img src="Kb.png" height = "250" /></td><td style="border: 1px black solid";><img src="Mo.png" height = "100"/> This is a complicated Fermi surface where small pockets of the Fermi surface indicate that the Fermi energy cuts through several bands at a steep angle. <img src="Mob.png" height = "250"/></td>
</tr><tr>
<td style="border: 1px black solid";><img src="Scan.png" height = "100"/> This is a hexagonal crystal. This is the only crystal with a different symmetry from the others so the symmetry points must be different from the other three. The Fermi level cuts through two bands at a low angle measure there is a large smooth Fermi surface indicating that there are many states close to the Fermi energy. <img src="Scanb.png" height = "250" /></td><td style="border: 1px black solid";><img src="Ba.png" height = "100"/> The volume of the Fermi sphere is almost the same as the volume of the first Brillouin zone. This metals has two valence electrons and the lowest band is almost completely filled (the yellow part) while a few electrons are occupied in the second band (the purple part). 
<img src="Bak.png" height = "250"/></td>
</tr>
</table>

(c) A wavefunction has the form $\psi_{k}(x) = e^{ikx}u_{k}(x)$ where $k$ is in the second Brillouin zone. $k = k' +G$ where $k'$ is in the first Brillouin zone and $G= \frac{2\pi}{a}$ is a reciprocal lattice vector. The wavefunction is,

$$e^{i(k'+G)x}u_{k}(x)$$

This can be written as, $e^{ik'x}u_{k'}(x)$ where,

$$u_{k'}(x)= e^{iGx}u_{k}(x)=e^{i\frac{2\pi x}{a}}u_{k}(x)$$

$e^{-iGx}u_{k}(x)$ would also be correct.

(d) Symmetric matrices have the property that the matrix elements $\chi_{ij}=\chi_{ji}$. The electric susceptibility is,

$$\chi_{ij} = -\frac{\partial ^2G}{\partial E_i \partial E_j} = \chi_{ji}$$

Since the order of the differentiation does not matter, $\chi_{ij}=\chi_{ji}$. This is independent of any symmetries that the point group may have.

(e) The piezoconductivity describes how the electrical conductivity changes as the stress on the crystal changes.

$$P_{ijkl} = \frac{\partial s_{ij}}{\partial \sigma_{kl}}$$

Here $P_{ijkl}$ is the piezo conductivity, $s_{ij}$ is the electrical conductivity, and $\sigma_{kl}$ is the stress. Since electrical conductivity and stress are both matricies, piezoconductivity is a fourth rank tensor. This problem is complicated by the fact that the symbol $\sigma$ is typically used for both the electrical conductivity and the stress. You have to redefine one of them in a problem like this.

PHY.K02 Solid State Physics27.06.2024

PHY.K02 Solid State Physics
27.06.2024