Problem 1
A hydroxyl radical consists of one hydrogen atom and one oxygen atom. Oxygen has 8 protons.

(a) Write down a trial wavefunction for the molecular orbital Hamilitonian of a hydroxyl radical. Justify your choice of atomic orbitals.

(b) How would the molecular orbitals generated by your trial wavefunction be filled in the ground state of the hydroxyl radical?

(c) How would you calculate the rotational energy levels of a hydroxyl radical? How many rotational modes are there?

(d) Is the bond in a hydroxyl radical a: single bond? double bond? covalent bond? ionic bond? van der Waals bond? sigma bond? pi bond? polar bond?

Problem 2

Consider a body centered cubic crystal with one atom in the basis. The lattice constant of the conventional unit cell is $a=$ 2 Å.

(a) The reciprocal lattice vectors are indexed using the conventional (cubic) primitive lattice vectors. What is the length of the reciprocal lattice vector $|\vec{G}_{112}|$?

(b) What phonon mode has the shortest wavelength? Hint: $\overline{\Gamma N}=\frac{\sqrt{2}\pi}{a},\,\overline{\Gamma P}=\frac{\sqrt{3}\pi}{a},\,\overline{\Gamma H}=\frac{2\pi}{a}$

(c) How may phonon normal modes are there in 1 cm³ of the bcc crystal?

(d) X-rays with a wavelength of 1.5 Å are used in a diffraction experiment. What is the largest reciprocal lattice vector that can be measured with these x-rays?

Problem 3

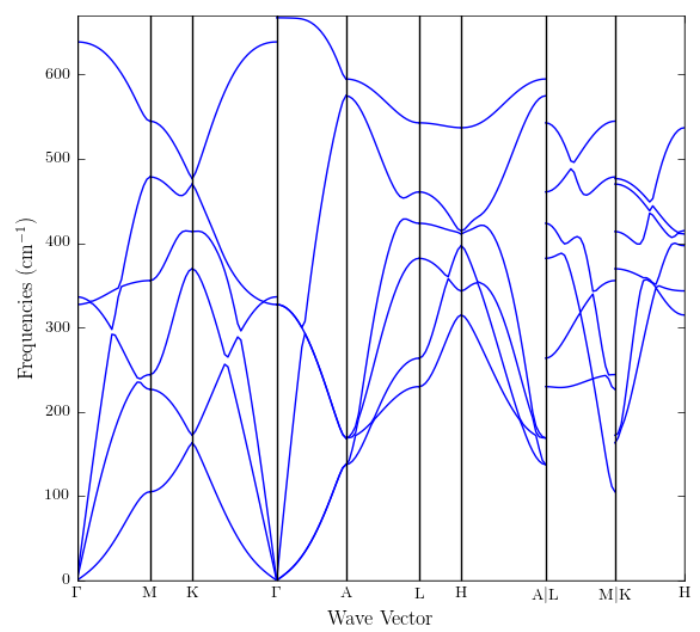
A phonon dispersion relation is shown to the right.

(a) How many atoms are there in the basis of this crystal? The symmetry points imply that this crytals has a hexagonal Bravais lattice. What crystal structure could this be?

(b) What is the highest frequency phonon mode in Hz?

(c) Label the Transverse Acoustic (TA) and the Longitudinal Acoustic (LA) modes in the $\Gamma -A$ directionand state how many Transverse Acoustic modes and how many Longitudinal Acoustic modes for every $\vec{k}$-value are there.

(d) If you knew the phonon density of states for copper and quartz (SiO₂), you could calculate the specific heat of quartz but not copper. Why?

Problem 4

An electron band structure is shown below. The bands with energies above $E =0$ are empty and the bands with energies less than $E =0$ are occupied.

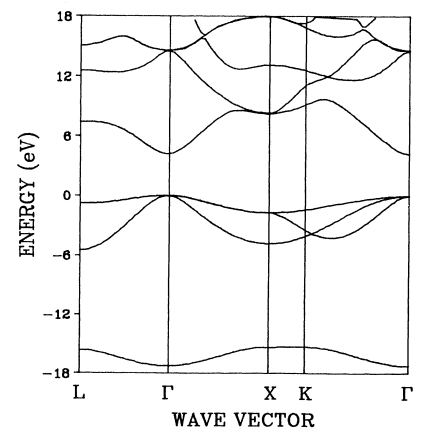
(a) Is this material a metal, a semiconductor, or an insulator?

(b) What is the chemical potential of this material?

(c) Does this material have a direct band gap?

(d) Estimate the ratio of the heavy hole mass to the light hole mass, $m_{hh}/m_{lh}$.